AN ANALYSIS OF DEFORMATION OF LABORATORY PLATE-TYPE SAMPLES UNDER A COMPLEX STRESS STATE

Высоконагруженные детали машин и элементы конструкций в процессе их эксплуатации подвергаются комплексу статических или циклических нагрузок, создающих объёмное напряженно-деформированное состояние (НДС), характеризуемое концентрацией напряжений вблизи конструктивных неоднородностей (отверстий, выступов, пазов и т. п.), вблизи которых могут располагаться очаги разрушений. Возникающее вблизи таких зон НДС, точнее, его уровень и вид определяют ресурс работы конструкции

В качестве теоретической основы для оценки прочности материала используются объединённые критерии прочности, структура которых описывается так называемыми уравнениями предельного состояния, к которым можно отнести известные уравнения Писаренко-Лебедева, Ягна-Бужинского, Друккера-Прагера и др.

В предложенной работе в качестве критерия подобия напряжённого состояния, возникающего в деформируемых объектах и в соответствующих им образцах для испытаний, используется коэффициент П – параметр напряженного состояния, равный отношению первого инварианта тензора напряжений ко второму

(1)

где σ1, σ2, σ3 – главные напряжения, возникающие в очаге возможного разрушения; σi – эквивалентное напряжение, определяемое формулой

(2)

Проблемой, возникающей при выполнении оценки конструкционной прочности на основе объединенных критериев прочности, является сложность создания в лабораторных образцах для механических испытаний вида НДС, характеризуемого различным соотношением инвариантов НДС в соответствии с неравенствами

(3)

Стоит отметить, что наиболее опасное с точки зрения зарождения и развития дефектов является соотношение инвариантов НДС, соответствующее положительным значениям (растягивающим) компонент главных напряжений, для которого П = 2.

В настоящее время для оценки прочности материала в условиях сложного НДС существуют множество конфигураций образцов, имеющие различной формы выемки, канавки или вырезы

Возможность повышения точности и достоверности моделирования конструкционной прочности материала открывается с помощью современных технологий моделирования и конструирования на основе метода конечных элементов. Предложена конфигурация образца, способного воспроизводить в своей рабочей зоне изменение коэффициента П в диапазоне (3). Конструкция образца представлена на рис. 1 и имеет форму круглой пластины с концентраторами напряжений в виде диаметрально расположенных U- или V-образных канавок (далее – пластинчатый образец). В процессе испытаний пластинчатого образца он опирается по своей наружной кромке (см. рис. 2) и при этом в его рабочей зоне, расположенной в центре круглой пластины на поверхности нижней U-образной канавки, может создаваться НДС, соответствующее одному из неравенств (3).

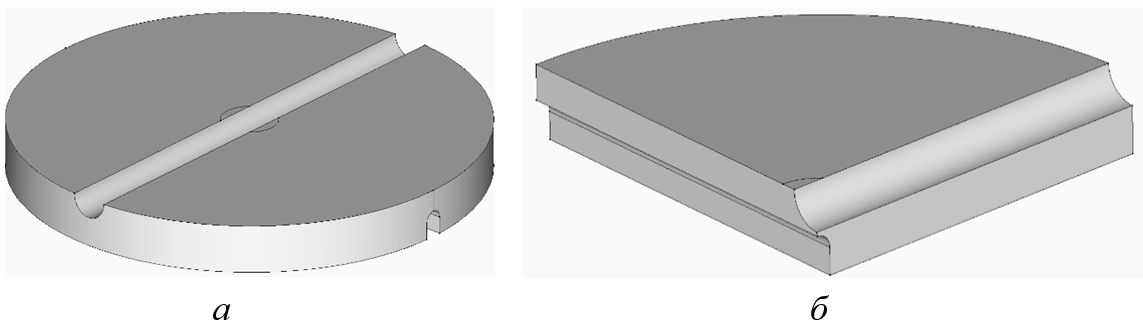
Рисунок 1 - Конструкция пластинчатого образца:

a – общий вид; б – четверть образца, высеченная из него двумя плоскостями симметрии

DOI:10.23670/IRJ.2023.127.103.1

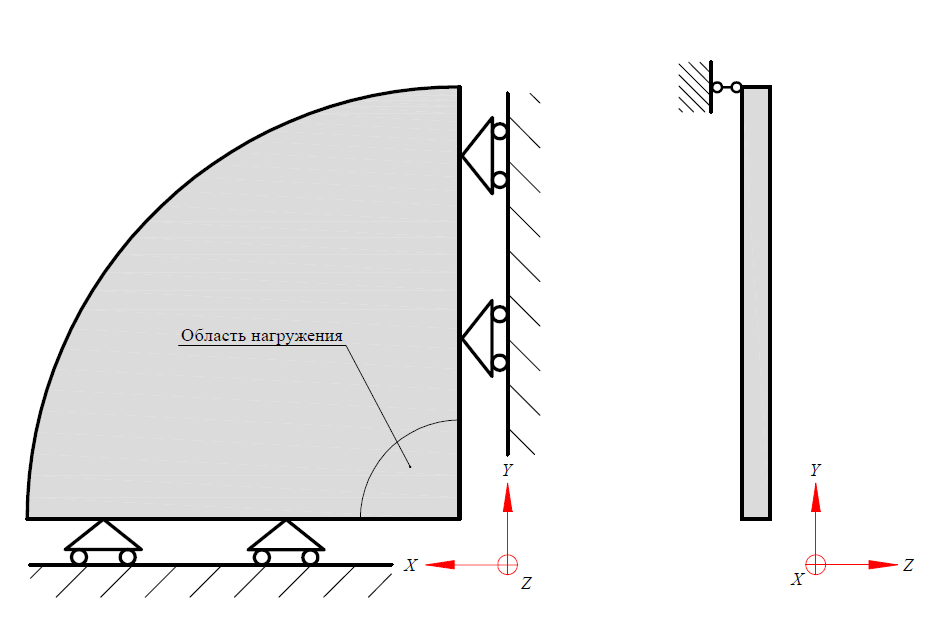
Рисунок 2 - Условия закрепления и нагружения пластинчатого образца

DOI:10.23670/IRJ.2023.127.103.2

В процессе механических испытаний образец опирается по своему наружному круговому контуру (на рис. 1 – стороной опирания является нижняя сторона круговой пластины). В своей центральной части образец в процессе испытаний нагружается вертикальной направленной вниз (перпендикулярно срединной поверхности круговой пластины) силой. Указанная сила распределяется в процессе испытаний на стороне нагружения образца по малой круговой поверхности в центральной части образца (круговой сектор на рис. 2).

При проведении вычислительных экспериментов по выявлению зависимостей изменения вида НДС образцов от геометрических параметров образцов использовалась математическая модель объемного упругого деформирования. В случае однородного изотропного материала эта модель определяется дифференциальными уравнениями равновесия теории упругости u

(4)

где L – дифференциальный оператор теории упругости;

u – искомый вектор перемещений в точках области D, занимаемой деформируемыми элементами конструкции;

λ, μ – коэффициенты, которые определяют механику однородного изотропного материала исследуемой конструкции (параметры Ламе).

Уравнение (4) рассматривается в области, занимаемой материалом образца и ограниченной поверхностью S = Sσ + Suσ, при краевых условиях

(5)

где Sσ, Suσ, – поверхности рассматриваемых образцов, на которых заданы поверхностные перемещения, поверхностные силы и смешанные (контактные) краевые условия соответственно;

Т – тензор напряжений;

F(M) – вектор поверхностных сил, заданный на поверхности Sσ;

ν, τ – единичные вектора, определяющие нормальное и касательное направления к поверхности S в точке М.

Моделирование НДС конструктивных вариантов пластинчатых образцов проводилось с помощью программного средства Femap (with NX Nastran). Для минимизации вычислительных ресурсов ЭВМ и повышения точности расчетных характеристик НДС выполнялась дискретизация четвертой части пластинчатых образцов с заданием соответствующих граничных условий кинематического закрепления. Дискретизация получаемых КЭ-моделей выполнялась на основе гексаэдра первого порядка аппроксимации и управляемой локализации сгущения разбивки КЭ-сетки (рис. 3). Указанная дискретизация позволила обеспечить относительную погрешность сходимости получаемых расчетных характеристик НДС не более 5%. Общее количество КЭ в используемых расчетных моделях в среднем не превысило 110 тыс.

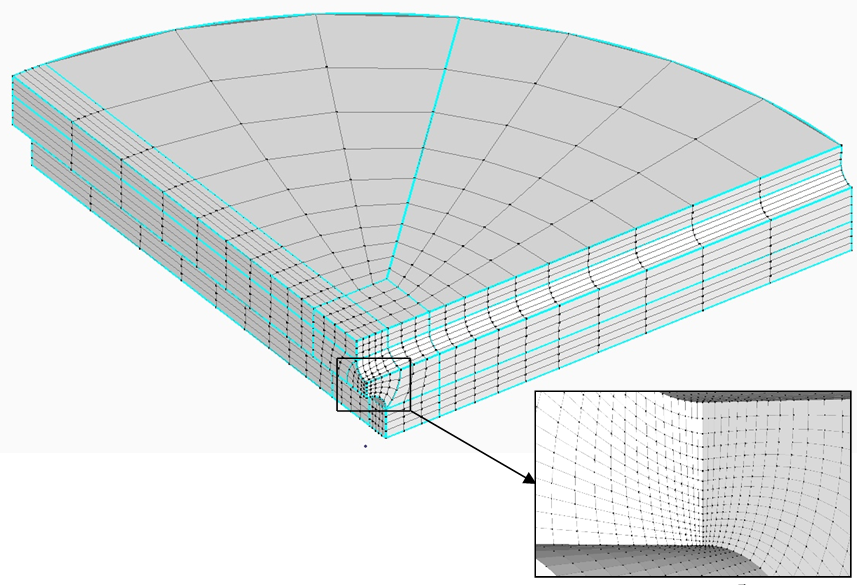
Рисунок 3 - Дискретная модель четверти пластинчатого образца

DOI:10.23670/IRJ.2023.127.103.3

В вычислительных экспериментах на наружной кромке образцов-прототипов ставились краевые условия, соответствующие закреплению в пространстве точек этой кромки в осевом направлении (см. рис. 2). Нагружение выполнялось приложением к центральной части образцов единичного давления, распределённого в пределах окружности диаметром, равным четверти диаметра верхней поверхности образца. При упругом объемном деформировании свойства материала принимались равным: модуль Юнга E = 210000 МПа и коэффициент Пуассона ν = 0,3, массовая плотность ρ = 7,85Е-9 тонн/м3.

При численном моделировании НДС рассматривались варианты пластинчатых образцов, способные воспроизводить значения величин Kσ и П, характерных для реальных конструкций

(6)

В формуле (6) σimax – эквивалентные напряжения в рабочей зоне; σiном – номинальные эквивалентные напряжения – интенсивность напряжений в центре аналогично нагруженного пластинчатого образца-прототипа без канавок-концентраторов на его сторонах (аналогичного по диаметру и толщине). Для представленных образцов наружный диаметр принимался неизменным и равным D = 200 мм, толщина – Н = 20 мм.

В вычислительных экспериментах рассматривались следующие диапазоны изменения варьируемых значений геометрических параметров (рис. 4)

(7)

где Н – толщина образца, Rн – радиус канавки на стороне нагружения образца, Rо – радиус канавки на стороне опирания образца, Z – расстояние от рабочей зоны до срединной поверхности образца, взятое с минусом, если рабочая располагается ниже срединной и с плюсом – выше срединной поверхности. В рассмотрение брались следующие безразмерные геометрические параметры: ρн – относительный радиус канавки на стороне нагружения образца; ρо – относительный радиус канавки на стороне опирания образца; ζ – относительное смещение рабочей зоны в направлении от срединной поверхности образца.

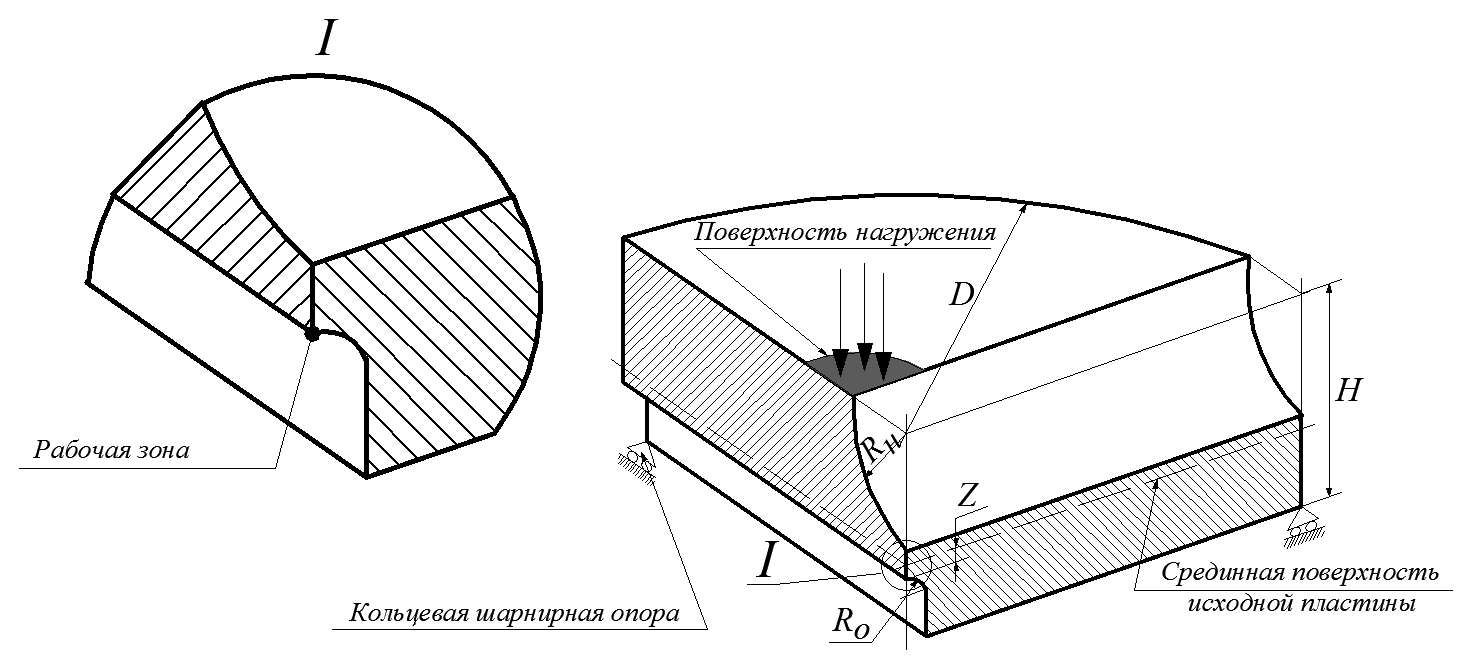
Рисунок 4 - Геометрические параметры пластинчатого образца-прототипа:

I – рабочая зона образца

DOI:10.23670/IRJ.2023.127.103.4

На рис. 5 представлен один из результатов численного моделирования упругого НДС образцов пластинчатого типа в виде распределения интенсивности напряжений σi.

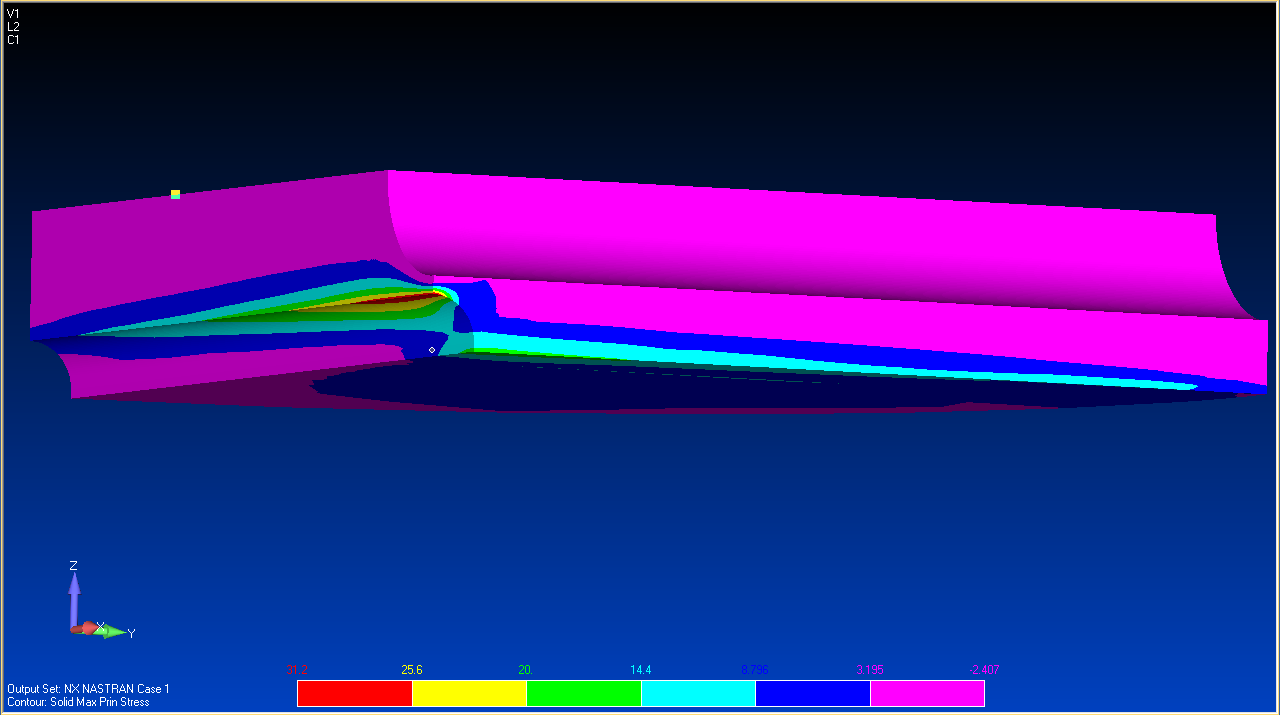
Рисунок 5 - Распределение интенсивности напряжений σi в пластинчатом образце

DOI:10.23670/IRJ.2023.127.103.5

На рис. 6 и рис. 7 приведены диаграммы вариантных исследований расчетных характеристик НДС пластинчатых образцов при их упругом объемном деформировании методом конечных элементов.

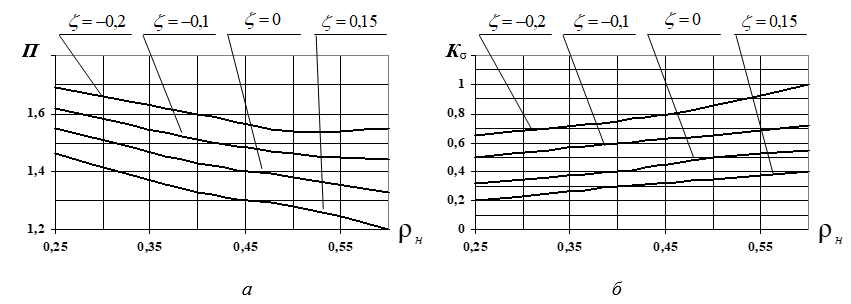
Рисунок 6 - Распределение коэффициентов П (а) и Kσ (б) от основных геометрических параметров образцов-прототипов при ρo=0,15

DOI:10.23670/IRJ.2023.127.103.6

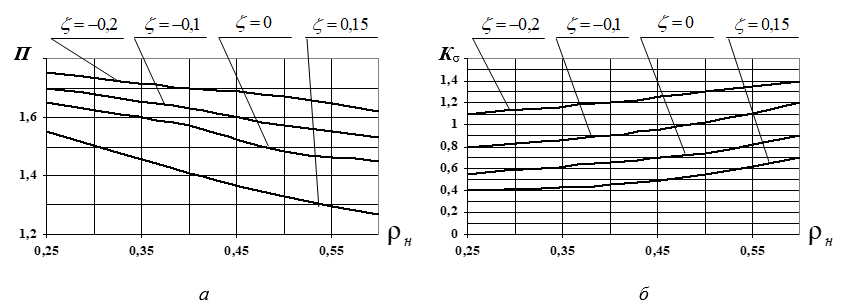
Рисунок 7 - Распределение коэффициентов П (а) и Kσ (б) от основных геометрических параметров образцов-прототипов при ρo=0,25

DOI:10.23670/IRJ.2023.127.103.7

На рис. 6, а и рис. 6, б приведены расчетные распределения значений П и Kσ в рабочей зоне пластинчатых образцов-прототипов при фиксированных значениях относительного радиуса канавки на стороне опирания ρо = ρоmin = 0,15, на рис. 7, а и рис. 7, б – при ρо=ρоmax = 0,25. Как следует из результатов вычислительных экспериментов, величина П изменяется в пределах от 1,2 до 1,75 (рис. 6 и рис. 7). Установлено, что концентрация напряжений Kσ имеет достаточно низкое значение (изменяется в пределах 0,2 < Kσ < 1,4). Выявленный диапазон изменения геометрических параметров пластинчатых образцов не приводит к необходимому изменению величины П во всём диапазоне, описываемом неравенствами (3).

Полученные результаты в совокупности позволяют выявить такие конфигурации пластинчатых образцов, для которых характеристики НДС (параметры П и Kσ) удовлетворяют диапазону, описываемому неравенствами (3). Исследованные образцы с концентраторами напряжений в виде U-образных канавок позволяют моделировать напряжённые состояния, управляемый вид которого принимает значения в диапазоне от 1,2 до 1,75 в зависимости от значений ширины и глубины U-образных канавок.