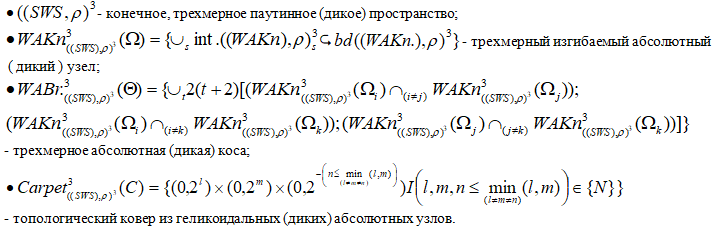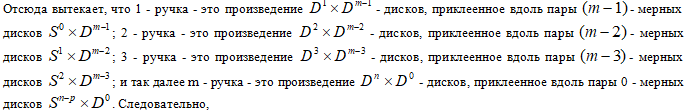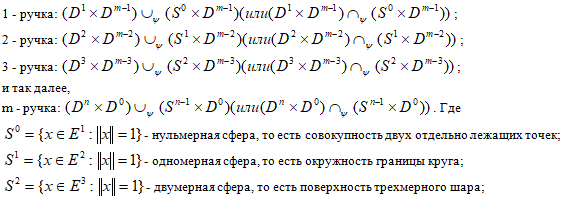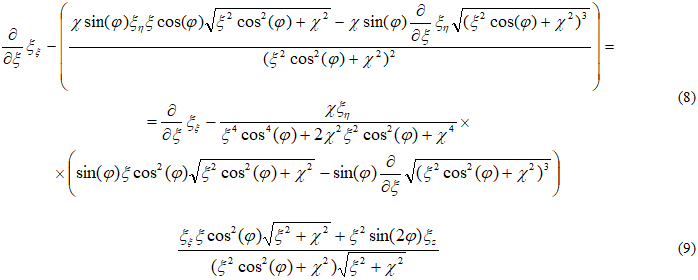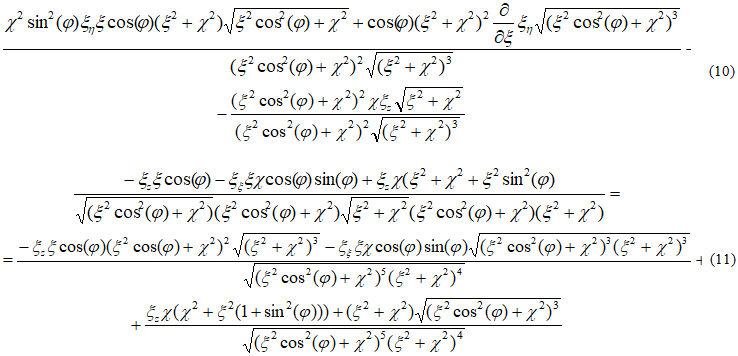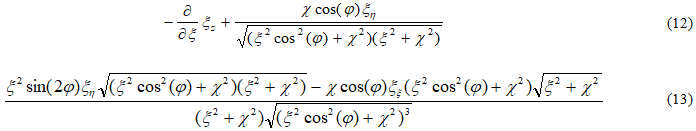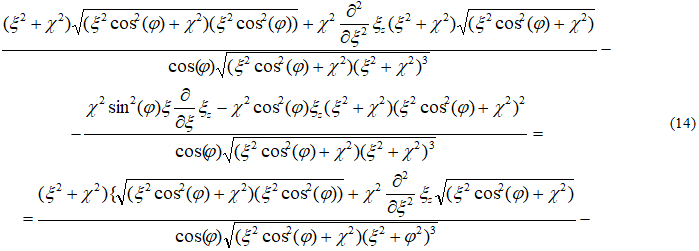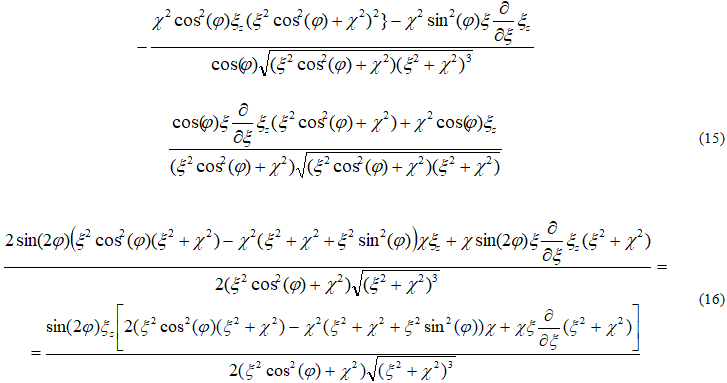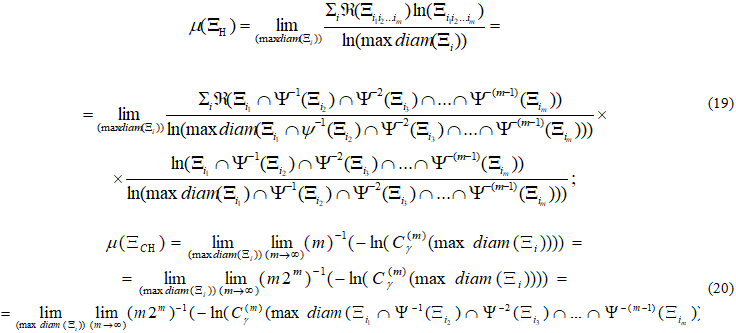Our journals
Submit manuscript Sign in / Sign up
Advanced search
Article sections

GEOMETRY OF WILD KNOTS AND WILD BRAIDS IN THREE-DIMENSIONAL WEBLIKE SPACE

Research article
Abdymanapov Usen
DOI:
https://doi.org/10.23670/IRJ.2021.103.1.001
Issue: № 1 (103), 2021
Published:
2021/01/22
PDF

ГЕОМЕТРИЯ АБСОЛЮТНЫХ (ДИКИХ) УЗЛОВ И КОС В ТРЕХМЕРНОМ ПАУТИННОМ ПРОСТРАНСТВЕ

Обзорная статья

Абдыманапов Усен*

ORCID: 0000-0002-5569-6266,

Международный юридический институт (МЮИ), Москва, Россия

* Корреспондирующий автор (u670913[at]mail.ru)

Аннотация

В данной статье описан оригинальный способ построения аналога - ожерелья Луи Августа Антуана в окрестности выколотых точек на минимальной поверхности винтовых кривых изгибаемых абсолютных (диких) узлов посредством заузленных зацеплений 1- ручек и вероятностных мер Хаоса, размерности Хаусдорфа, относящихся ко всей совокупности наблюдаемых событий по всему направлению трехмерного паутинного пространства. Для исследования патологических свойств и геликоидальных структур изгибаемых абсолютных (диких) узлов и кос, выявления особенностей топологического ковра впервые применен метод “Плетение с винтовым кручением” и наиболее яркие перспективы его дальнейшего развития.

Ключевые слова: абсолютный (дикий) узел, абсолютная (дикая) коса, паутинное пространство, топологический ковер из геликоидальных (диких) абсолютных узлов, плетение с винтовым кручением.

GEOMETRY OF WILD KNOTS AND WILD BRAIDS IN THREE-DIMENSIONAL WEBLIKE SPACE

Review article

Abdymanapov Usen*

ORCID: 0000-0002-5569-6266,

International Law Institute (MUI), Moscow, Russia

* Сorresponding author(u670913[at]mail.ru)

Abstract

This article describes an original method for constructing an analog of Antoine's necklace in the vicinity of empty dots on the minimal surface of helixes of bent wild knots by means of knotted looping of 1-handles and the chaos probability measures with Hausdorff dimension that are related to the entire set of observed events in the entire direction of three-dimensional weblike space. In order to explore the pathological properties and helicoidal structures of bent wild knots and braids and to identify the features of the topological carpet, the study for the first time applies the method of “lattice with helical curvature” and demonstrates the distinct prospects for its further development.

Keywords: wild knot, wild braid, web space, topological carpet of helicoidal wild knots, lattice with helical curvature.

Введение

В 1921 году под руководством Анри Леона Лебега (Henri Leon Lebesgue) Луи Август Антуан (Louis Auguste Antoine) защитил докторскую диссертацию на тему «О гомеоморфности двух фигур и двух окрестностей», среди результатов которой было построение ожерелья, являющегося вложением канторова множества в трехмерном пространстве и обладающее неодносвязным дополнением. То есть дикий узел, содержащий более сложное множество – «ожерелье Луи Августа Антуана», получается, как пересечение убывающей последовательности компактных множеств:

01-03-2021 16-47-39 - такой, что каждое 01-03-2021 16-47-46 является объединением конечного числа непересекающихся полноториев. Если максимальный диаметр полнотория в 01-03-2021 16-47-46 стремится к нулю при 01-03-2021 16-47-52 то есть 01-03-2021 16-48-07 является компактным вполне несвязным множеством без изолированных точек, гомеоморфное канторову множеству. При желании можно выбрать последовательность 01-03-2021 16-47-46 так, что дополнение к полученному 01-03-2021 16-48-30 неодносвязно и пересечение 01-03-2021 16-48-38 с каждым полноторием в 01-03-2021 16-47-46 образует замкнутую цепь [11]. Такое вложение канторова множества в трехмерном пространстве представляется неоценимым вкладом для развития маломерной топологии и не теряет свои актуальности вплоть до сегодняшнего дня. С тех пор и по сей день интерес к ожерелью Луи Августа Антуана со стороны исследователей-топологов не угасает, возникают новые современные проблемы:

  • Если заузлить зацеплением 1 - ручки окрестности выколотых точек на минимальной поверхности винтовых линий изгибаемых абсолютных (диких) узлов, то сохранится ли устойчивость этих винтовых линий?
  • В топологическом ковре трансверсальные точки при деформации изгибаемых геликоидальных абсолютных (диких) узлов соединяются ли петлями одинаковой площадью независимо от азимутальных углов?
  • Сферические спирально винтовые абсолютные (дикие) узлы с разъединенными концами, зацепляясь между собой в пары, тройки и более образуют ли колье подобно ожерелью Луи Августа Антуана?
  • При переплетении в косу изгибаемые геликоидальные абсолютные (дикие) узлы допускают ли деформацию по кругу с точностью до раздутий и стягиваний?

Эти четыре проблемы определяют цель данной статьи. Проведенное исследование показывает, что ответ утвердительный. Основные идеи и положения статьи содержатся в докладах и в работах автора [1], [10].

Актуальность, теоретическая и практическая значимость работы

Актуальность исследования геометрии изгибаемых абсолютных (диких) узлов и кос в трехмерном паутинном пространстве обусловлена тем, что она является обобщенной моделью Антуана компакта трехмерного пространства, привлекающего на протяжении почти века внимание геометров, топологов и физиков. Несмотря на то, что работа носит теоретический характер, полученные в ней результаты могут быть использованы в различных задачах маломерной топологии, спирально винтовой геометрии и топологии, а также в архитектурно - строительной инженерии при строительстве высотных спирально винтовых сооружений (где устойчивость витков сооружений играет важную роль).

Напоминаем, что узел называется ручным, если существует его расширение до полнотория 01-03-2021 16-55-40, допускающее вложение в 3 - сферу. А дикими называются узлы, содержащие дуги Фокса - Артина - некоторые простые дуги, полученные диким вложением в трехмерное евклидово пространство 01-03-2021 16-55-48. Также легко можно построить дикий узел, содержащий не только одну, а несколько патологических точек, образующих канторово множество. Если для любых двух непрерывных функций 01-03-2021 16-56-13 существует гладкая кривая кривизна и кручения которой определяются уравнениями кривой

01-03-2021 16-56-21    (1)

то уравнения кривой (1) не зависят от выбора системы координат. Поэтому кривая определена уравнениями кривой (1) однозначно с точностью до перемещения в пространстве. Следовательно, уравнения пространственной кривой (1) задают её кривизну и кручения с учётом того, что отношение кручения к кривизне постоянно. По сути дела, кривизна — это мера отклонения кривой от касательной, а кручение — это мера отклонения кривой от соприкасающейся плоскости. Но, с другой стороны, для координатных функций кривой имеет место уравнение

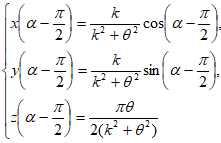01-03-2021 16-56-29     (2) которое определяет винтовую линию, лежащую на круговом цилиндре 01-03-2021 16-56-53    (3)

Так как нормали в точках поверхности, образованной касательными к винтовой линии, образуют постоянный угол с осью винта, то чем больше мера отклонения кривой от соприкасающейся плоскости, тем кривая пространственнее. В противном случае кривая меньше отличается от плоской кривой. Подобно тому, что при винтовом движении точек образуются винтовые линии (цилиндрические, конические, сферические и гиперболические) и при винтовом движении отрезка прямой линии получается винтовая поверхность, можно получить винтовое геометрическое тело. Если какую-либо плоскую фигуру передвигать по поверхности круглого цилиндра так, чтобы вершины плоской фигуры перемещались по винтовым линиям, а плоскость плоской фигуры постоянно проходила через ось круглого цилиндра, то образуется винтовой выступ, ограниченный винтовыми и цилиндрическими поверхностями. Следовательно, построение такого винтового выступа сводится к построению стольких винтовых линий, сколько вершин у выбранной плоской фигуры. Из пространственных кривых линий, в технике широко применяются цилиндрические винтовые линии одинакового уклона - геликоиды.

Как геометрическая фигура, геликоид по своему значению по разнообразию форм и свойств не имеет себе равных. Иначе говоря, геликоид — это винтовая поверхность, описываемая параметрическими соотношениями, образованная движением прямой, вращающейся вокруг перпендикулярной к ней оси и одновременно поступательно движущейся в направлении этой оси с пропорциональной скоростью этих движений. Главной особенностью этой винтовой линии является минимальная величина, подвергаемая к любой деформации её площади при заданной внешней границе. Так как изгибание поверхности представляет собой топологическое отображение, то есть гомеоморфизм, который исключает сжатие и растяжение, то небольшую локальную область геликоида можно изометрически продеформировать в локальной области катеноида или однополостного гиперболоида.

Обозначения и основные понятия

Если иное не предусмотрено, то в этой работе будут применяться следующие понятия и обозначения:

01-03-2021 17-01-09

Определение 1. Паутинное (дикое) пространство — это множество расслоенных, изгибаемых геликоидальных паутин, наклоны которых к горизонтальной плоскости в поперечных сечениях, зависят только лишь от расстояний до оси винтовой развертки поверхности кривых линий в концентрические дуги, а не от азимутальных углов.

Определение 2. Абсолютный (дикий) узел — это деформированная минимальная поверхность, натянутая на винтовую линию и содержащая множество выколотых точек с окрестностью в ожерелье Луи Августа Антуана, патологически вложенная в трехмерное паутинное (дикое) пространство.

Определение 3. Абсолютная (дикая) коса — это трёхмерный пучок, состоящий из “m” - прядей изгибаемых абсолютных (диких) узлов, в которых непересекающиеся между собой выпуклые и вогнутые касательные точки над и под пересечениями, пересекают каждый изгибаемый абсолютный (дикий) узел однократно, и при этом допускают сплетение с точностью до 2(m+2) (m повторений.

Определение 4. Топологический ковер из геликоидальных (диких) абсолютных узлов — это с высокой точностью и толщиной переплетенные между собой множества изгибаемых абсолютных (диких) узлов, сотканные соответственно с 01-03-2021 17-12-38 продольными и поперечными слоями, состоящими из множества четных и нечетных выколотых точек минимальной поверхности, попарно перекрученные на целое число оборотов дикими 1 - ручками по винтовой минимальной поверхности вдоль оси изгибаемых абсолютных (диких) узлов.

Определение 5. Геометрическое шарообразное трёхмерное тело со спирально винтовым выступом — это шарообразный спирально винтовой геликоид с бесконечным числом витков, ограниченный сферически спиральной поверхностью, расстояние между витками которого уменьшено до минимума по мере приближения их к полюсам.

Геометрические и геликоидальные структуры изгибаемых абсолютных (диких) узлов и кос в трехмерном паутинном (диком) пространстве

Согласно теории Э. Артиновой кос [12] одной из важных задач топологии является проблема узлов и ее обобщение. Если можно считать, что узел — это непрерывная замкнутая пространственная кривая без двойных точек, то деформация определяется, как непрерывное видоизменение этой кривой без самопересечения, и любой узел тогда под влиянием деформации переходит в окружность. Под плетением нитей (или шнурков) в косы или косой “ m “ - го порядка понимается следующий топологический образ [12].

Пусть в пространстве дан прямоугольник с противоположными сторонами 01-03-2021 17-15-09 01-03-2021 17-14-55 - длины и - ширины. И пусть на каждой из обеих сторон - длины даны “m“ - точки, соответственно 01-03-2021 17-15-32 причем направление нумерации идет от ширины сторон прямоугольника 01-03-2021 17-15-47 к ширине сторон прямоугольника 01-03-2021 17-15-57. Тогда в каждой точке 01-03-2021 17-16-23 длины стороны прямоугольника 01-03-2021 17-16-30 однозначно ставится в соответствие некоторая точка 01-03-2021 17-16-39 длин сторон прямоугольника 01-03-2021 17-16-50, соединенные между собой с пространственной кривой 01-03-2021 17-16-58 без двойных точек, которые не пересекаются ни одной из кривых 01-03-2021 17-17-06. Следовательно, пространственная кривая 01-03-2021 17-16-58 ориентирована от точки 01-03-2021 17-16-23 длины сторон прямоугольника 01-03-2021 17-16-30 к точке 01-03-2021 17-16-39 длины сторон прямоугольника 01-03-2021 17-16-50. Далее классическая техника плетения кос производится по разработанному алгоритму. Более изящный способ переплетения кос принадлежит американскому топологу, одному из создателей теории узлов - Джеймсу Уэнделлу Александеру. Некоторые тонкие соображения из этого способа применены в работах [13], [14].

В случае конечного паутинного (дикого) трёхмерного пространства в качестве пространственной кривой, мы возьмем пучок изгибаемых абсолютных (диких) узлов. Когда говорим об изгибаемом абсолютном (диком) узле, то под этим понятием мы понимаем следующие:

Предположим, что 01-03-2021 17-23-14 - некоторое многообразие в произвольной степени. И, пусть 01-03-2021 17-23-05 - мерный шар ( или  01-03-2021 17-23-22 -  мерный круглый цилиндр), что 01-03-2021 17-23-34 Тогда существует гомеоморфизм 01-03-2021 17-23-43 01-03-2021 17-23-58.

01-03-2021 17-27-50

01-03-2021 17-29-07

и так далее,

01-03-2021 17-31-34 -  - мерная сфера, то есть поверхность - мерного шара.

Абсолютный (дикий) узел представляет собой спирально винтовое изгибаемое трёхмерное тело с той разницей, что его винтовые минимальные поверхности переплетены с диким заузленным ожерельем Луи Августа Антуана и выколоты круглыми дырками. Если пронумеровать все выколотые круглые дырки на винтовом выступе по круговому квадранту:

01-03-2021 17-32-13 чередующиеся с нечетными и четными числами, то каждая малая окрестность винтовой толщины, образует двумерный диск 01-03-2021 17-32-24, а сжимающиеся к центру узкие окрестности винтовой толщины образуют настолько малый диск 01-03-2021 17-32-34, что множество 01-03-2021 17-32-45 попарно не пересекается. Следовательно, отображение 01-03-2021 17-32-54 есть вращение вокруг начала координат на угол 01-03-2021 17-33-04. Таким образом, 01-03-2021 17-33-18 - малый двумерный диск 1 - ручки с “m“ - выколотыми круглыми дырками на винтовом выступе изгибаемого абсолютного (дикого) узла. Так как 1 - ручки на винтовом выступе зацеплены между собой

01-03-2021 17-36-28    (4)

то все заузленные и зацепленные друг с другом 1 - ручки могут быть перекручены на целое число оборотов, так как поверхность винтового выступа ориентируема. Из вышесказанного приходим к выводу, что винтовая поверхность, натянутая на винтовую линию, сохраняет устойчивость.

 Напоминаем, что в классическом понимании коса из “m” - прядей нити (или шнурка) — это геометрический объект, состоящий из двух параллельных плоскостей в трехмерном (универсальном) пространстве, содержащий упорядоченные множества в равном количестве точек, соответствующих двум параллельным плоскостям, и из “m”  - непересекающихся между собой простых дуг, соединяющих упорядоченные множества точек, пересекающих каждую параллельную плоскость однократно.

Следовательно, коса из “m”  - прядей нити (или шнурка) — это геометрический объект, который абстрактно (или визуально) описывает переплетение косы из “m”  - прядей нити (или шнурка) между собой в длину.

Метод «плетение с винтовым кручением (или плетение с винтовым кручением, равномерно сжимающимся в направлении к центральной оси по круговому квадранту)»

Для наглядности возьмем шарообразный трёхмерный пучок, состоящий из множества всех изгибаемых абсолютных (диких) узлов, проходящих через одну и ту же ось пересечений и разобьём его на шесть взаимно перпендикулярных направляющих полуосей со множеством “m” - прядей. Выберем одну из шести направляющих полуосей со множеством прядей, состоящих из всех изгибаемых абсолютных (диких) узлов, каждый из которых по прямой винтовой поверхности развёртывается в концентрические дуги, при одном и том же фиксированном центральном угле. Так как

  • витки изгибаемого абсолютного (дикого) узла с правой винтовой поверхностью, получаются при разрезке кольца произвольной толщины, угол которого вращается с кручением по круговому квадранту на симметричных пределах 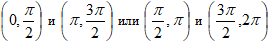01-03-2021 17-38-38 с возвратно - поступательным перемещением, или наоборот, и откладывается на наружной стороне винтовой поверхности от радиальной линии, в направлении по ходу часовой стрелки;
  • витки изгибаемого абсолютного (дикого) узла с левой винтовой поверхностью, получаются при разрезке кольца произвольной толщины, угол которого вращается с кручением по круговому квадранту на симметричных пределах 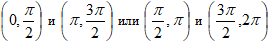01-03-2021 17-38-38 с возвратно - поступательным перемещением, или наоборот, и откладывается на наружной стороне винтовой поверхности от радиальной линии, в направлении против хода часовой стрелки;

то при плетении абсолютной (дикой) косы из “m” - прядей изгибаемых абсолютных (диких) узлов с правой винтовой поверхностью, либо с левой винтовой поверхностью, либо одновременно с чередующимися правыми и левыми винтовыми поверхностями, следует добиваться к коллинеарным вложениям витков (включая компланарные барьеры между витками с чередующимся плетением над и под пересечениями изгибаемых абсолютных (диких) узлов) с помощью бесконечного изгибания, деформируя концентрические дуги проходящие под, либо над пересечениями изгибаемых абсолютных (диких) узлов по круговому квадранту  01-03-2021 17-38-38. Такой процесс плетения абсолютной (дикой) косы из “m”- прядей изгибаемых абсолютных (диких) узлов продолжается до тех пор, пока не заплетётся вся её длина. Алгоритм метода аналогичным образом применим ко всем остальным пяти взаимно перпендикулярным направляющим полуосям со множеством “m“ - прядей.

Замечание 1. Если точку пересечения всех плотно переплетённых абсолютных (диких) кос, шарообразного трёхмерного пучка перекрутить одновременно по вертикальным и по горизонтальным полуосям до самого конца, то получим плотный трёхмерный шар с закрученным винтовым выступом.

Классическая техника плетения абсолютной (дикой) косы с применением метода «плетение с винтовым кручением (или плетение с винтовым кручением, равномерно сжимающимся в направлении к центральной оси по круговому квадранту)»

Классическая техника плетения абсолютной (дикой) косы с применением нового метода, рассматривается в конечном паутинном (диком) трёхмерном пространстве в следующих вариантах:

01-03-2021 17-41-30 плетение абсолютной (дикой) косы из “m” - прядей изгибаемых абсолютных (диких) узлов с правой винтовой поверхностью;

01-03-2021 17-41-38плетение абсолютной (дикой) косы из “m” - прядей изгибаемых абсолютных (диких) узлов с левой винтовой поверхностью;

01-03-2021 17-41-45плетение абсолютной (дикой) косы из “m” - прядей изгибаемых абсолютных (диких) узлов совместно с правыми и с левыми, или наоборот, винтовыми поверхностями.

Переплетение абсолютной (дикой) косы из “m”- прядей с изгибаемыми абсолютными (дикими) узлами в вариантах (01-03-2021 17-41-30) и (01-03-2021 17-41-38 ), кроме варианта (01-03-2021 17-41-45) с применением нового метода, никакого особого труда не составляет. Наиболее интересен (01-03-2021 17-41-45) - вариант. Так как плетение девичьей косы начинается из трёх прядей, состоящих из нескольких волосинок, то мы рассмотрим (01-03-2021 17-41-45) - вариант по аналогии девичьей косы со следующими частными случаями и его обобщение до “m“ - й пряди.Замечание 2. В качестве геометрического объекта для плетения абсолютной (дикой) косы возьмём шарообразный трёхмерный пучок, состоящий из множества изгибаемых абсолютных (диких) узлов.

  1. Классическое плетение абсолютной (дикой) косы из трёх прядей с абсолютными (дикими) узлами с применением метода - плетение с винтовым кручением.
01-03-2021 17-44-35

процесс плетения повторяется через каждые шесть шагов.

  1. Классическое плетение абсолютной (дикой) косы из четырёх прядей с абсолютными (дикими) узлами с применением метода - плетение с винтовым кручением.
01-03-2021 17-45-52 01-03-2021 17-46-03

процесс плетения повторяется через каждые восемь шагов.

  1. Классическое плетение абсолютной (дикой) косы из пяти прядей с абсолютными (дикими) узлами с применением метода - плетение с винтовым кручением.
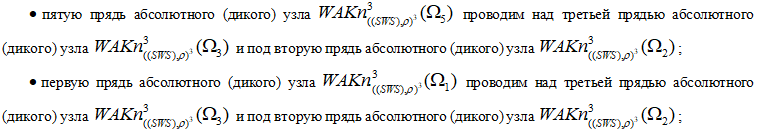
01-03-2021 17-49-08 01-03-2021 17-49-23

процесс плетения повторяется через каждые десять шагов.

  1. Классическое плетение абсолютной (дикой) косы из шести прядей с абсолютными (дикими) узлами с применением метода - плетение с винтовым кручением.
  • все пряди множества абсолютных (диких) узлов, шарообразного трёхмерного пучка переложим на одну направляющую полуось из шести взаимно перпендикулярных между собой направляющих полуосей, и разделим их на левую и на правую часть;

01-03-2021 17-51-57 01-03-2021 17-52-19

процесс плетения повторяется через каждые двенадцать шагов.

  1. Классическое плетение абсолютной (дикой) косы из семи прядей с абсолютными (дикими) узлами с применением метода - плетение с винтовым кручением.
  • разобьем шарообразный трёхмерный пучок со множеством прядей из абсолютных (диких) узлов на семь одинаковых частей и разделим их на левую и на правую стороны;
01-03-2021 17-55-17 01-03-2021 17-55-39

процесс плетения повторяется через каждые четырнадцать шагов.

  1. Классическое плетение абсолютной (дикой) косы из восьми прядей с абсолютными (дикими) узлами с применением метода - плетение с винтовым кручением.
01-03-2021 17-58-51 01-03-2021 17-59-11 01-03-2021 17-59-37

процесс плетения повторяется через каждые шестнадцать шагов.

  1. Классическое плетение абсолютной (дикой) косы из девяти прядей с абсолютными (дикими) узлами с применением метода - плетение с винтовым кручением.
  • весь шарообразный трёхмерный пучок со множеством прядей из абсолютных (диких) узлов переложим раскидывая назад, соединив их концы в одну общую точку и получим по виду напоминающий вытянутый к вершине круглый конус, слегка полувогнутый вовнутрь с выпуклым основанием и разобьем его по периметру поверхности на левую, центральную и правую одинаковые части;
01-03-2021 18-03-35
  • отделив из левой части шестую прядь абсолютного (дикого) узла 01-03-2021 18-05-55, протянем её над ближайшей соседней прядью абсолютного (дикого) узла , под следующей прядью абсолютного (дикого) узла и снова над ещё соседней прядью абсолютного (дикого) узла;
  • седьмую прядь абсолютного (дикого) узла 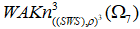01-03-2021 18-06-08 уложим над соседней прядью абсолютного (дикого) узла, протянем её под следующей прядью абсолютного (дикого) узла и вновь над очередной прядью абсолютного (дикого) узла и в итоге, все пряди абсолютных (диких) узлов будут располагаться в две стороны;
  • восьмую прядь абсолютного (дикого) узла 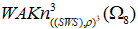01-03-2021 18-06-35 проводим под ближайшей соседней прядью абсолютного (дикого) узла, затем над следующей прядью абсолютного (дикого) узла, вновь под и над очередной прядью абсолютных (диких) узлов;
  • в конце концов каждую новую прядь абсолютных (диких) узлов переплетаем с ближайшими третьими прядями абсолютного (дикого) узла 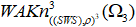01-03-2021 18-06-51 и четвёртыми прядями абсолютного (дикого) узла 01-03-2021 18-06-59, чередуя положение плетений над и под, и переплетение завершится в том и только в том случае, если все пряди абсолютных (диких) узлов центральной части будут располагаться в одну из трёх частей;
  • девятую прядь абсолютных (диких) узлов 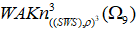01-03-2021 18-07-07 проводим под ближайшей прядью абсолютных (диких) узлов, затем уложим её над следующей прядью абсолютного (дикого) узла и вновь под очередной прядью абсолютного (дикого) узла;
  • к крайней прядке абсолютных (диких) узлов добавим небольшую часть абсолютных (диких) узлов, взятую в одной из трёх частей (точнее из левой части), и уложим их все вместе под прядью абсолютного (дикого) узла, над прядью абсолютного (дикого) узла, чередуя положение плетений и, так далее;
  • доведём до конца плетение основной пряди абсолютных (диких) узлов вместе с добавленной частью из левой части, где множество прядей абсолютных (диких) узлов, располагается по разные стороны;
  • аналогичным образом проведём переплетение с добавленными прядями абсолютного (дикого) узла из правой части;
  • вновь заплетаем, пока не закончатся свободные пряди абсолютных (диких) узлов и дальше будем формировать косичку, заплетая ее без добавочных прядей абсолютных (диких) узлов;
  • процесс плетения повторяется через каждые восемнадцать шагов.
  1. Классическое плетение абсолютной (дикой) косы из “m” - прядей с абсолютными (дикими) узлами с применением метода - плетение с винтовым кручением.
  • аналогичным образом плетутся абсолютные (дикие) косы 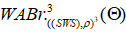01-03-2021 18-11-56 из нескольких “m“ - прядей изгибаемых абсолютных (диких) узлов;
  • техника плетения абсолютной (дикой) косы 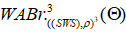01-03-2021 18-11-56, остается прежней;
  • процесс плетения повторяется через каждые 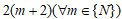01-03-2021 18-12-06 шагов.

Наиболее яркие перспективы метода - плетение с винтовым кручением, и его дальнейшее развитие

Вновь возьмём шарообразный трёхмерный пучок, состоящий из “m” - прядей множества всех изгибаемых абсолютных (диких) узлов, проходящих через одну и ту же ось пересечения, и разобьём их

на три взаимно перпендикулярные оси, или на шесть взаимно перпендикулярных направляющих полуосей со множеством 01-03-2021 18-28-34   - прядей;

на пять взаимно перпендикулярных осей, или на десять взаимно перпендикулярных направляющих полуосей со множеством 01-03-2021 18-28-57 - прядей;

на девять взаимно перпендикулярных осей, или на восемнадцать взаимно перпендикулярных направляющих полуосей со множеством 01-03-2021 18-28-46 - прядей;

  на семнадцать взаимно перпендикулярных осей, или на тридцать четыре взаимно перпендикулярных направляющих полуосей со множеством 01-03-2021 18-29-05 - прядей, и так далее.

Очевидно, что разности между последующими и предыдущими взаимно перпендикулярными осями со множеством “ m “ - прядей, представляются рядами геометрической прогрессии

01-03-2021 18-29-17

но, с другой стороны, количество чисел, взаимно перпендикулярных направляющих полуосей со множеством “ m “ - прядей, также представляется неполными рядами геометрической прогрессии с отсутствием первого члена ряда

01-03-2021 18-29-30

Произвольным образом, можно переплетать абсолютную (дикую) косу  01-03-2021 18-29-43 из шарообразного трёхмерного пучка, состоящего из множества “m” - прядей изгибаемых абсолютных (диких) узлов 01-03-2021 18-29-50, проходящих через одну и ту же ось винтовых кривых, по всем его взаимно перпендикулярным направляющим полуосям. От произвольного значения угла наклона оси винтовой развёртки поверхности кривых в концентрические дуги, то есть от поверхности, представляющей геометрическое место главных нормалей винтовой линии, получим

плотно закрученный с переплетением абсолютный (дикий) шар с винтовым выступом;

плотно закрученный с переплетением абсолютный (дикий) эллипсоид с винтовым выступом;

конически переплетённый абсолютной (дикой) косой, продолговатый круглый конус с винтовым скрученным выступом.

Но, с другой стороны, если предположим параметрическое уравнение поверхности, представляющее геометрическое место главных нормалей винтовой линии в виде

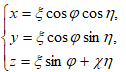01-03-2021 18-33-23    (7)

в цилиндрической системе координат, в которой за координату ξ примем расстояние по образующей, а за координаты соответственно η - угол вращения образующей и  φ - угол наклона образующей поверхности, представляющий геометрическое место главных нормалей винтовой линии, то в смысле А.Л. Гольденвейзера [15] очевидно получим аналогичное геометрическое соотношение

01-03-2021 18-34-54

01-03-2021 18-38-21

01-03-2021 18-38-38

01-03-2021 18-38-52

01-03-2021 18-41-00

В дополнение к этому можно подчерпнуть некоторые соображения в [16].

Изгибающие континуумы с относительной метрикой, деформируемые в сферически спиральный абсолютный (дикий) узел

По сути дела, абсолютная (дикая) коса  01-03-2021 18-11-56, переплетённая из всех множеств прядей изгибаемых абсолютных (диких) узлов 01-03-2021 18-29-50 является частным случаем голографической спиральной (дикой) косы 01-03-2021 18-51-22, переплетённой из всех множеств голографических спиральных (диких) узлов 01-03-2021 18-51-32, изгибающих континуумы с относительной метрикой, и путь познания природы таких узлов, несомненно, лежит через познание их патологических структур и свойств. Геометрическая томография множеств голографических спиральных (диких) узлов 01-03-2021 18-51-32, изгибающих континуумы с относительной метрикой и переплетенных ими голографических спиральных (диких) кос 01-03-2021 18-51-22 представляется плотно скрученным к центральной оси симметрии улитковым фракталом, причем, каждая его сканированная часть допускает геометрическую и топологическую структуру. Непрерывно деформируя изгибающие континуумы с относительной метрикой, получим сферически спиральные изгибаемые абсолютные (дикие) узлы 01-03-2021 18-51-54 с разъединёнными концами двигающимися в конечном трёхмерном паутинном (диком) пространстве 01-03-2021 18-52-08 случайно с равной вероятностью, с конечным числом раскладок и объёмов.

Замечание 3. Трёхмерная сферическая (или шарообразная) спираль — это винтовая кривая на поверхности сферы (или внутри плотного шара), пересекающая все меридианы сферы (или шара) под постоянным углом и имеющая бесконечное число витков, в которой расстояние между витками убывает по мере приближения к полюсам. В качестве такого трёхмерного винтового кривого выступает изгибаемый абсолютный (дикий) узел с параметрическим уравнением:

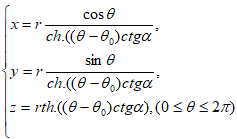01-03-2021 18-56-20    (17)

где ch. и th. - гиперболические косинус и тангенс.

Заметим, что сферически спиральные изгибаемые абсолютные (дикие) узлы 01-03-2021 18-57-15 с разъединёнными концами допускают геометрические структуры и метрические аппроксимации со сферически спиральными дикими точками, и мера хаоса при этом, представляется с точностью до случайных перемещений, не имеющих общей цели:

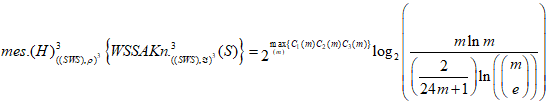01-03-2021 18-57-24       (18)

где 01-03-2021 18-57-35 - число случайных перемещений.

Так как компактное множество 01-03-2021 18-57-45, сотканных топологических ковров из геликоидальных (диких) абсолютных узлов, не разбивается на два и более непересекающихся инвариантных подмножества 01-03-2021 19-00-19, и в то же время оно разбивается на конечное число измеримых подмножеств, то размерность Хаусдорфа 01-03-2021 18-57-51 и размерность хаоса 01-03-2021 18-58-04 соответственно будут равны

01-03-2021 19-00-55

Основные результаты

Все изложенные выше исследования, естественно, приводят к следующим равносильным эквивалентным утверждениям:

Предложение 1. Пусть задано конечное, трёхмерное паутинное (дикое) пространство 02-03-2021 10-43-45. И пусть 02-03-2021 10-43-56 - абсолютный (дикий) узел. Тогда следующие утверждения эквивалентны:

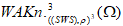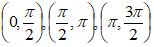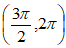  • абсолютный (дикий) узел 02-03-2021 10-44-24 представляет собой цилиндрически спирально винтовое или сферически спирально винтовое с разъединёнными концами геометрическое тело с винтовым выступом, каждый виток винтового выступа которого выколот круглыми дырками по круговому квадранту: 02-03-2021 10-44-36 и 02-03-2021 10-44-43 чередующимися чётными и нечётными числами;
  • так как 1 - ручки с “m” - выколотыми круглыми дырками на винтовом выступе могут быть зацеплены друг с другом, то каждая зацепленная друг с другом 1 - ручка, может быть перекручена на целое число оборотов;
  • число заклеенных 1 - ручек на спирально винтовом выступе не превосходит 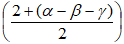02-03-2021 10-44-50, где α - число двойных точек на нормальной проекции, β - максимальное значение индекса пересечения Джордана 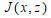02-03-2021 10-45-28 нескольких объединений замкнутых линий в трехмерном конечном паутинном(диком)пространстве, которые попарно не пересекаются друг с другом, γ - множество всех вырезанных круглых дырок;
  • поверхность винтового выступа абсолютного (дикого) узла 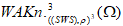02-03-2021 10-44-24, которая представляет собой либо цилиндрически спирально винтовое, либо сферически спирально винтовое с разъединёнными концами геометрическое тело, вытянутое вдоль винтовой линии, сохраняет устойчивость;
  • любой тип конфигурации абсолютных (диких) узлов 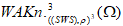02-03-2021 10-44-24 допускает геометрическую структуру и метрически аппроксимируемо либо цилиндрически спиральными, либо сферически спиральными соответственно точками;
  • сферически спирально винтовые абсолютные (дикие) узлы 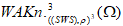02-03-2021 10-44-24 с разъединёнными концами зацепляясь между собой в пары, тройки и более образуют шарообразное колье;
  • любой тип конфигурации абсолютных (диких) узлов 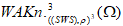02-03-2021 10-44-24, расположенных неравномерно и визуально в трёхмерном конечном паутинном (диком) пространстве 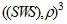02-03-2021 10-43-45, имеет меру хаоса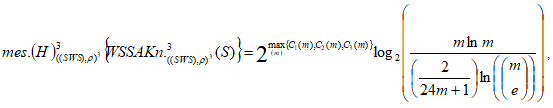 02-03-2021 11-06-17

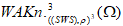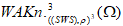где 02-03-2021 11-07-09 - число случайных перемещений, не имеющих общей цели, то есть любой тип конфигурации абсолютных (диких) узлов 02-03-2021 10-44-24 под влиянием деформации двигается в конечном трёхмерном паутинном (диком) пространстве 02-03-2021 10-43-45 случайно с равной вероятностью, а m - число раскладок любого типа абсолютных (диких) узлов 02-03-2021 10-44-24 в заданном конечном трёхмерном паутинном (диком) пространстве 02-03-2021 10-43-45.

Предложение 2. Пусть в трёхмерном конечном паутинном (диком) пространстве 02-03-2021 10-43-45 задано трёхмерная абсолютная (дикая) коса 02-03-2021 10-43-56 из “m“ - прядей абсолютных (диких) узлов 02-03-2021 10-44-24. И пусть 02-03-2021 11-13-55 - топологический ковер из геликоидальных (диких) абсолютных узлов. Тогда следующие утверждения эквивалентны:

  • всякое переплетение из “m“ - прядей любого типа конфигураций абсолютного (дикого) узла 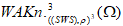02-03-2021 10-44-24, начиная с трёх и более - есть абсолютная (дикая) коса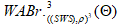01-03-2021 18-29-43  с различным типом плетения;
  • в топологическом ковре из геликоидальных (диких) абсолютных узлов 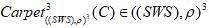02-03-2021 11-13-55 трансверсальные точки 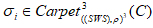02-03-2021 11-19-48  соединяются петлями одинаковой площадью, образуя пучкообразную мозаику кривых и на порядок отличаются от неподвижной точки 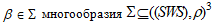02-03-2021 11-20-13, которое имеет сложную патологическую структуру;
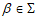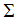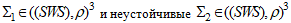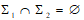  • неподвижная точка 02-03-2021 11-20-27 многообразия 02-03-2021 11-20-34 имеет соответственно, устойчивые 02-03-2021 11-20-57многообразия, не имеющие самопересечение 02-03-2021 11-21-03;
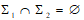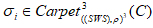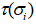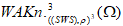  • если имеет место соотношение 02-03-2021 11-21-03, то петли, с помощью которых соединены трансверсальные точки 02-03-2021 11-19-48 посредством отображения 02-03-2021 11-21-14 вытягиваются до предельного касания соответственно между выпуклыми и вогнутыми касательными точек любого типа конфигураций абсолютного (дикого) узла 02-03-2021 10-44-24;
  • если же имеет место соотношение 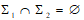02-03-2021 11-21-03, то возникают свободные (дикие) точки 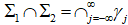02-03-2021 11-21-30, которые определяются бесконечным множеством пересечений;
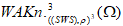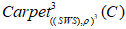  • локальную область любого типа конфигураций абсолютного (дикого) узла 02-03-2021 10-44-24 можно изометрически гладко подвергать к деформации в локальную область топологического ковра из геликоидальных (диких) абсолютных узлов 02-03-2021 11-29-50;
  • если компактное множество 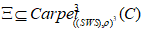02-03-2021 11-29-58 разбивается на конечное число измеримых подмножеств 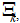02-03-2021 11-30-45, то размерность Хаусдорфа и размерность хаоса соответственно равны
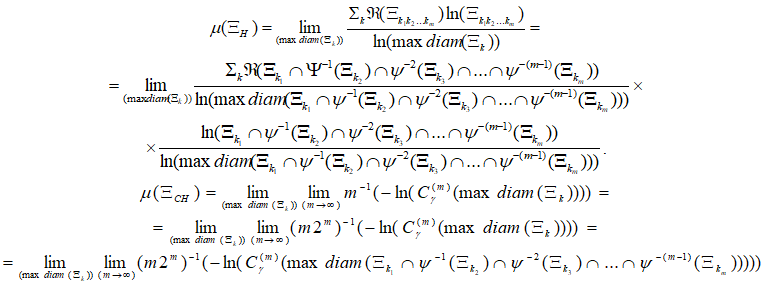
02-03-2021 11-32-04

Заключение

В полном объеме исследованы геометрические и геликоидальные структуры изгибаемых абсолютных (диких) узлов и кос в трёхмерном конечном паутинном (диком) пространстве. Построен топологический ковер из геликоидальных (диких) абсолютных узлов и особый тип геометрического трехмерного тела с винтовым выступом.

Конфликт интересов Не указан. Conflict of Interest None declared.

Список литературы / References

  1. Абдыманапов У. Дикое вложение звездного тело в трёхмерном Евклидовом пространстве / У. Абдыманапов // Наука и новые технологии. Нетрадиционные идеи и новые направления науки. - 2002.- № 4. - С.101-103.
  2. Abdymanapov U. Wild embeddings of the star body in three-dimensional Euclidean space (continued research) / U. Abdymanapov // 4th European Congress of Mathematics. - Stockholm: ICMS-Progress in Mathematics (- 2004/- vol.2004/- no.1).
  3. Abdymanapov U. Intersection of surfaces with skeletons in three-dimensional star space / U. Abdymanapov // Dubrovnik VII - Geometric Topology. Inter-University Centre. Dubrovnik and Department of Mathematics. University of Zagreb. - Dubrovnik. Groatia. - 2011. - P. 1-2.
  4. Abdymanapov U. Cobraidal braids / U. Abdymanapov // 46th Annual Spring Topology and Dynamics Conference. Univeridad Nacional Autonoma de Mexico (UNAM). Mexico City. D.F. - Mexico. - 2012. - P. 1-2.
  5. Abdymanapov U. Pathological ( wild ) knots and braids in three-dimensional of the Euclidean space / U. Abdymanapov // 28th Summer Conference on Topology and it’s Applications. Nipissing University. - Noth Bay. - Ontario. Canada - 2013. - 1-2.
  6. Abdymanapov U. Intersection of the spiral disks with skeletons in three-dimensional of the coral space / U. Abdymanapov // The 4th Abu Dhabi University. Annual International Conference: Mathematical Science and it’s Applications. - 2015. - Abu Dhabi. United Arab Emirates. - P. 1-2.
  7. Абдыманапов У. Патологические ( дикие ) узлы и косы в трёхмерном звёздном пространстве / У. Абдыманапов // Сборник трудов всероссийской научной конференции МИЕСЭКО-2016. - Москва. - Том 1. - 2016. - С. 20 - 33.
  8. Абдыманапов У. Геометрия поверхностей конфокальной системы в трёхмерном Евклидовом пространстве / У. Абдыманапов // Труды XLI Межд. научно-практической конференции “ Естественные и математические науки в современном мире “. - Новосибирск. - 2016. - № 4 (39). - С. 122 - 132.
  9. Abdymanapov U. Wild knots in the spiral braided continuum / U. Abdymanapov // 2016 International Conference of the Honam Mathematical Society. Chonbuk National University. - 2016. Jeonju. South Korea. - P. 1-2.
  10. Abdymanapov U. Wild knots in the spiral braided continuum (continued research) / U. Abdymanapov // International Conference on Application of Mathematics to Nonlinear Sciences. Association of Nepal Mathematicians in America and Nepal Mathematical Society. - 2016. - Kathmandu. - P. 1-2.
  11. Louis Auguste Antoine. Sur I’homeomorphisme de deux figures et leurs voisinages / Louis Auguste Antoine // Journal Math.Pures.-1921. et appl.4. - P. 221-325.
  12. Artin E. Abhandl aus dem / E. Artin // Mathem. Seminar. - Hamburg. - 1925. - vol. 4. - P. 47-72.
  13. Alexander J.W. On the deformation of n - cell / J.W. Alexander // Proc. Nat. Acad. Sc. USA. -1923. - vol. 9. - P. 406-407.
  14. Alexander J.W. The combinatorial theory of complexes / J.W. Alexander // Ann. Math. - 1930. - vol. 30. - P. 2092-2320.
  15. Гольденвейзер А.Л. Теория тонких упругих оболочек / А.Л. Гольденвейзер. - М.: ГТТИ. - 1953. -544c.
  16. Рекач В.Г. Расчёт оболочек сложной геометрии / В.Г.Рекач, С.Н.Кривошапка. // Монография. - М.: изд-во УДН. - 1988. -176 c.

Список литературы на английском языке / References in English

  1. Abdymanapov U. Dikoe vlozhenie zvezdnogo telo v trjohmernom Evklidovom prostranstve [Wild embeddings of the star body in three-dimensional Euclidean space] / U. Abdymanapov // Nauka i novye tehnologii. Netradicionnye idei i novye napravlenija nauki [Science and new technologies. Unconventional ideas and new directions of science]. - 2002.- № 4. - P.101-103. [in Russian]
  2. Abdymanapov U. Wild embeddings of the star body in three-dimensional Euclidean space (continued research) / U. Abdymanapov // 4th European Congress of Mathematics. - Stockholm: ICMS-Progress in Mathematics (- 2004/- vol.2004/- no.1).
  3. Abdymanapov U. Intersection of surfaces with skeletons in three-dimensional star space / U. Abdymanapov // Dubrovnik VII - Geometric Topology. Inter-University Centre. Dubrovnik and Department of Mathematics. University of Zagreb. - Dubrovnik. Groatia. - 2011. - P. 1-2.
  4. Abdymanapov U. Cobraidal braids / U. Abdymanapov // 46th Annual Spring Topology and Dynamics Conference. Univeridad Nacional Autonoma de Mexico (UNAM). Mexico City. D.F. - Mexico. - 2012. - P. 1-2.
  5. Abdymanapov U. Pathological ( wild ) knots and braids in three-dimensional of the Euclidean space / U. Abdymanapov // 28th Summer Conference on Topology and it’s Applications. Nipissing University. - Noth Bay. - Ontario. Canada - 2013. - P. 1-2.
  6. Abdymanapov U. Intersection of the spiral disks with skeletons in three-dimensional of the coral space / U. Abdymanapov // The 4th Abu Dhabi University. Annual International Conference: Mathematical Science and it’s Applications. - 2015. - Abu Dhabi. United Arab Emirates. - P. 1-2.
  7. Abdymanapov U. Patologicheskie ( dikie ) uzly i kosy v trjohmernom zvjozdnom prostranstve [Pathological ( wild ) knots and braids in three-dimensional of the star space] / U. Abdymanapov // Sbornik trudov vserossijskoj nauchnoj konferencii MIESJeKO-2016 [Proceedings of the Conference of Mathematics, Informatics, Natural Science in Economics and Society (CMINSES)]. - Moscow. - Vol 1. - 2016. - P. 20 - 33. [in Russian]
  8. Abdymanapov U. Geometrija poverhnostej konfokal'noj sistemy v trjohmernom Evklidovom prostranstve / U. Abdymanapov [The geometry of the surfaces of the confocal system in three –dimensional Euclidean space] // Trudy XLI Mezhd. nauchno-prakticheskoj konferencii “ Estestvennye i matematicheskie nauki v sovremennom mire” [Proceedings of the XLI International Scientific and Practical Conference “ Natural and mathematical sciences in the modern world”]. -Novosibirsk. - 2016. - no.4(39). - P.122 - 132. [in Russian]
  9. Abdymanapov U. Wild knots in the spiral braided continuum / U. Abdymanapov // 2016 International Conference of the Honam Mathematical Society. Chonbuk National University. - 2016. Jeonju. South Korea. - P. 1-2.
  10. Abdymanapov U. Wild knots in the spiral braided continuum (continued research) / U. Abdymanapov // International Conference on Application of Mathematics to Nonlinear Sciences. Association of Nepal Mathematicians in America and Nepal Mathematical Society. - 2016. - Kathmandu. Nepal. - P. 1-2.
  11. Louis Auguste Antoine. Sur I’homeomorphisme de deux figures et leurs voisinages [On the homeomorphism of two figures and their neighbourhoods] / Louis Auguste Antoine // Journal Math.Pures.-1921. et appl.4. - P. 221-325. [in French]
  12. Artin E. Abhandl aus dem [Abhandl from the] / E. Artin // Mathem. Seminar. - Hamburg. - 1925. - vol. 4. - P. 47-72. [in German]
  13. Alexander J.W. On the deformation of n - cell / J.W. Alexander // Proc. Nat. Acad. Sc. USA. -1923. - vol. 9. - P. 406-407.
  14. Alexander J.W. The combinatorial theory of complexes / J.W. Alexander // Ann. Math. - 1930. - vol. 30. - P. 2092-2320.
  15. Gol'denvejzer A.L. Teorija tonkih uprugih obolochek [Theory of thin elastic shells] / A.L. Gol'denvejzer. - M.: GTTI. - 1953. -544 p. [in Russian]
  16. Rekach V.G. Raschjot obolochek slozhnoj geometrii [Calculation of shells of complex geometry] / V.G.Rekach, S.N.Krivoshapka. - M.: Publishing House of UDN. - 1988. -176 p. [in Russian]