ИССЛЕДОВАНИЕ СЕМЕЙСТВ СОФОКУСНЫХ ЭЛЛИПСОВ И ГИПЕРБОЛ СРЕДСТВАМИ МАТЕМАТИЧЕСКОГО ПАКЕТА GEOGEBRA
ИССЛЕДОВАНИЕ СЕМЕЙСТВ СОФОКУСНЫХ ЭЛЛИПСОВ И ГИПЕРБОЛ СРЕДСТВАМИ МАТЕМАТИЧЕСКОГО ПАКЕТА GEOGEBRA
Научная статья
Российский технологический университет, Москва, Россия
* Корреспондирующий автор (elenavladpronina[at]rambler.ru)
АннотацияВ статье приведено задание семейств софокусных эллипсов и гипербол и исследование их свойств средствами математического пакета GeoGebra в курсе «Аналитической геометрии» при изучении темы «Кривые второго порядка» студентами технического вуза. Основной целью статьи является демонстрация интеграции современных информационных технологий в процесс преподавания высшей математики. С помощью встроенных инструментов и команд среды GeoGebra поэтапно показано задание и построение софокусных эллипсов и гипербол. С использованием динамических чертежей рассмотрен процесс «трансформации» одной коники в другую при различных значениях задаваемых параметров. Опираясь на свойства касательных к кривым второго порядка, установлено и исследовано, что софокусные эллипс и гипербола пересекаются под прямым углом. Последний результат рассмотрен для различных случаев взаимного расположения кривых и касательных к ним, проведённых в точке их пересечения. Все полученные результаты обоснованы строго математически.
Ключевые слова: GeoGebra, преподавание математики, кривые второго порядка, эллипс, гипербола, касательные к коникам, оптические свойства коник, софокусные коники, углы между кривыми.
THE RESEARCH ON THE FAMILIES CONFOCAL ELLIPSES AND HYPERBOLAS THROUGH GEOGEBRA MATHEMATICAL PACKAGE
Research article
Pronina E.V.*
Russian Technological University, Moscow, Russia
* Corresponding author (elenavladpronina[at]rambler.ru)
AbstractThe article describes setting the families of confocal ellipses and hyperbolas and studying their properties through the GeoGebra mathematical package in the course "Analytic geometry" under the topic "Second-order curve" by the students of a technical college. The primary purpose of the article is to demonstrate the integration of modern information technology into the process of teaching higher mathematics. Using the built-in tools and commands of the GeoGebra environment, the setting and construction of confocal ellipses and hyperbolas are shown step-by-step. Using the dynamic drawings, the author considers the process of "transformation" of one conic into another at different values of the specified parameters. Relying on the properties of a tangent to a second-order curve, the author found and analyzed that the confocal ellipse and the hyperbola intersect at a right angle. The last result is considered for various cases of the mutual arrangement of curves and tangents at the point of their intersection. All the results obtained are justified strictly mathematically.
Keywords: GeoGebra, teaching mathematics, second-order curves, ellipse, hyperbola, tangents to conics, optical properties of conics, confocal conics, angles between curves.
ВведениеВ курсе «Аналитическая геометрия» в техническом вузе предусмотрено изучение темы «Кривые второго порядка». Для решения сложных задач, выходящих за рамки программы, к сожалению, не всегда остаётся время. Одним из таких вопросов является вопрос рассмотрения софокусных коник и их свойств. Его рассмотрение удобно организовать с помощью динамических чертежей математического пакета GeoGebra, позволяющего моделировать и решать различные геометрические задачи, проводить анализ геометрической конфигурации объектов, строить графики функций, получать изображения плоских фигур и устанавливать связи между их элементами, проводить дополнительные построения, создавать анимацию рисунков.
Динамичность используемой математической среды полностью отвечает современным запросам общества для быстрого, правильного и наглядного получения результата, проверки гипотез. В результате подобной интеграции современных информационных технологий в образовательный процесс вуза происходит приобщение студентов к исследовательской деятельности средствами научных разработок в области информатики, что позволяет повысить мотивацию обучения и общую компьютерную грамотность обучающихся.
Процесс моделирования задачи, её пошаговое результативно-визуальное решение с помощью динамических чертежей способствует систематизации, глубокому пониманию и усвоению теоретических основ темы, а также, формированию навыков, связанных с применением математических методов в конструировании объектов.
Исследование общих свойств софокусных коник средствами пакета GeoGebra
В этом разделе рассмотрим общее задание софокусных коник и изучим процесс трансформации одной коники в другую средствами пакета GeoGebra. Поскольку основной целью статьи является демонстрация интеграции пакета GeoGebra в учебный процесс, будем приводить обоснования получаемых результатов.
Зададим на плоскости две точки ![]() . Не нарушая общности, будем полагать, что они находятся на оси абсцисс. Рассмотрим семейство всех эллипсов и гипербол, для которых
. Не нарушая общности, будем полагать, что они находятся на оси абсцисс. Рассмотрим семейство всех эллипсов и гипербол, для которых ![]() являются фокусами. Такие эллипсы и гиперболы называются софокусными. Центры эллипса и гиперболы совпадают и находятся в начале координат. Большая ось эллипса и действительная ось гиперболы находятся на оси Ox, малая ось эллипса и мнимая ось гиперболы находятся на оси Oy.
являются фокусами. Такие эллипсы и гиперболы называются софокусными. Центры эллипса и гиперболы совпадают и находятся в начале координат. Большая ось эллипса и действительная ось гиперболы находятся на оси Ox, малая ось эллипса и мнимая ось гиперболы находятся на оси Oy.
Уравнение произвольной линии рассматриваемого семейства можно записать в виде ![]() – каноническое уравнение семейства софокусных эллипсов и гипербол. При этом параметр
– каноническое уравнение семейства софокусных эллипсов и гипербол. При этом параметр ![]() .
.
Реализация в среде GeoGebra
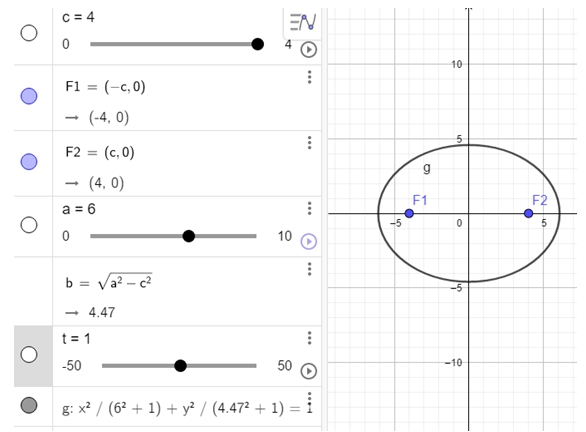
Шаг 1. Зададим значение параметра c (для примера произвольно, например, c=4)
В строке ввода введём с=4.
Для дальнейших исследований можно задать диапазон значений параметра c. Для этого необходимо выбрать появившийся «бегунок» ![]() и установить границы изменения параметра, например, от 0 до 4.
и установить границы изменения параметра, например, от 0 до 4.
Шаг 2. Зададим фокусы
В строке ввода введём F1=(-c,0).
В строке ввода введём F2=(c,0).
Шаг 3. Зададим значение параметра a (для примера произвольно, соблюдая )
В строке ввода введём a=6.
Шаг 4. Зададим значение параметра b
В строке ввода введём ![]()
Шаг 5. Зададим значение параметра t. В качестве начального значения выберем t=0.
В строке ввода введём ![]()
Шаг 6. Теперь непосредственно зададим конику.
В строке ввода введём ![]()
Результат выполнения шагов 1-6 представлен на рисунке 1.
Рис. 1 – Результат выполнения шагов 1-6
Рассмотрим возможные значения параметра t.
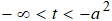 . В этом случае
. В этом случае 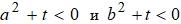 . Очевидно, нет точек плоскости, координаты которых удовлетворяли бы уравнению кривой.
. Очевидно, нет точек плоскости, координаты которых удовлетворяли бы уравнению кривой.
Рассмотрим случай 1 в среде GeoGebra.
Шаг 7. Для параметра t введём границы изменения, например, от -50 до ![]() с шагом 1, см. рисунок 2.
с шагом 1, см. рисунок 2.
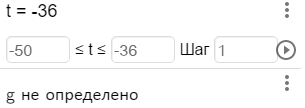
Рис. 2 – Результат выполнения шага 7
Нажав на кнопку ![]() , запустим бегунок и убедимся, что нет точек плоскости, координаты которых удовлетворяли бы заданному параметру. Обратите внимание, при
, запустим бегунок и убедимся, что нет точек плоскости, координаты которых удовлетворяли бы заданному параметру. Обратите внимание, при ![]() для g появляется значение «не определено».
для g появляется значение «не определено».
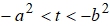 . В этом случае множеством точек плоскости, удовлетворяющим заданию кривой g, является гипербола. С действительной полуосью
. В этом случае множеством точек плоскости, удовлетворяющим заданию кривой g, является гипербола. С действительной полуосью 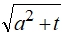 и мнимой полуосью
и мнимой полуосью 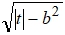 .
.
Рассмотрим случай 2 в среде GeoGebra.
Шаг 8. Для параметра t введём границы изменения от ![]() с шагом 1.
с шагом 1.
Нажав на кнопку ![]() , запустим бегунок и убедимся, что при каждом значении параметра t получается гипербола. Можно заметить, что при
, запустим бегунок и убедимся, что при каждом значении параметра t получается гипербола. Можно заметить, что при ![]() слева, гипербола сжимается к оси Ox, что соответствует уменьшению мнимой полуоси гиперболы. При
слева, гипербола сжимается к оси Ox, что соответствует уменьшению мнимой полуоси гиперболы. При ![]() справа, гипербола сжимается к оси Oy, что соответствует уменьшению действительной полуоси гиперболы.
справа, гипербола сжимается к оси Oy, что соответствует уменьшению действительной полуоси гиперболы.
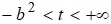 . В этом случае множеством точек плоскости, удовлетворяющим заданию кривой g, является эллипс. С большой полуосью
. В этом случае множеством точек плоскости, удовлетворяющим заданию кривой g, является эллипс. С большой полуосью 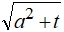 и малой полуосью
и малой полуосью 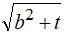 .
.
Рассмотрим случай 3 в среде GeoGebra.
Шаг 9. Для параметра t введём границы изменения от ![]() до, например, 50 с шагом 1.
до, например, 50 с шагом 1.
Нажав на кнопку ![]() , запустим бегунок и убедимся, что при каждом значении параметра t получается эллипс. Можно заметить, что при
, запустим бегунок и убедимся, что при каждом значении параметра t получается эллипс. Можно заметить, что при ![]() справа, большая полуось эллипса стремится к c, тогда как малая стремится к нулю и эллипс сжимается к оси Ox. При
справа, большая полуось эллипса стремится к c, тогда как малая стремится к нулю и эллипс сжимается к оси Ox. При ![]() эллипс «округляется», поскольку его эксцентриситет стремится к единице.
эллипс «округляется», поскольку его эксцентриситет стремится к единице.
Если теперь для параметра t задать границы изменения, например, от -50 до 50 с шагом 1, то можно с помощью динамического чертежа проследить весь процесс трансформации, описанный в случаях 1-3 и реализованный в шагах 7-8.
Приложение свойств касательных к семействам софокусных коник
В этом разделе, используя пакет GeoGebra, исследуем экспериментально один очень интересный результат, относящийся к семейству софокусных коник и часто остающийся за пределами вузовской программы.
- Постановка задачи
Доказать, что любые эллипс и гипербола из семейства софокусных коник пересекаются под прямым углом.
Углом между двумя пересекающимися кривыми называется угол между касательными к ним в точке их пересечения.
Будем считать, что фокусы коник расположены на оси Ox. В этом исследовании предусмотрим случай, когда центр эллипса и гиперболы может быть смещён относительно начала координат, при этом оси симметрии эллипса и гиперболы остаются параллельны осям Ox и Oy.
На первом шаге зададим фокусы, затем вычислим половину фокусного расстояния c. Для обобщения результатов исследования, длину большой полуоси эллипса и главной оси гиперболы будем задавать в некоторых границах больше или меньше параметра c соответственно.
Далее рассмотрим решение задачи только в среде GeoGebra.
- Реализация в среде GeoGebra
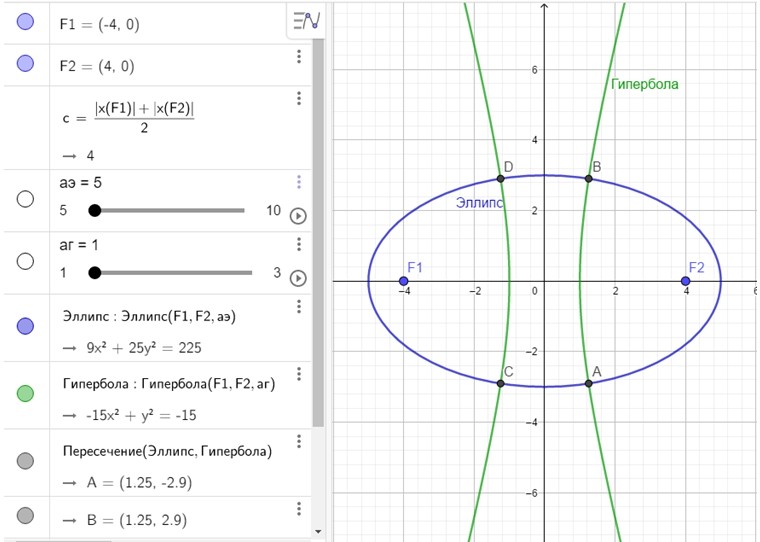
Шаг 1. Зададим фокусы эллипса и гиперболы.
В строке ввода введём F1=(-4,0) и F2=(4,0) (например).
Шаг 2. Вычислим половину фокусного расстояния c.
В строке ввода введём с=(abs(x(F1))+ abs(x(F2)))/2.
Шаг 3. Зададим большую полуось эллипса, назвав её аэ.
В строке ввода введём аэ=5 (например).
Далее, нажав на появившийся бегунок, зададим границы изменения большой полуоси от c+1 до 10 (например), шаг 1.
Шаг 4. Зададим действительную полуось гиперболы, назвав её аг.
В строке ввода введём аг=3 (например).
Далее, нажав на появившийся бегунок, зададим границы изменения действительной полуоси от 1 до с-1 (например), шаг 1.
Шаг 5. Построим эллипс.
В строке ввода введём Эллипс(F1,F2,аэ).
Изменим цвет, например, на синий. Для этого необходимо щёлкнуть правой кнопкой мыши на кривой, далее выбрать Настройки→Цвет.
Шаг 6. Построим гиперболу.
В строке ввода введём Гипербола(F1,F2,аг).
Изменим цвет, например, на зелёный.
Шаг 7. С помощью инструмента ![]() «Точка»→«Пересечение», найдём точки пересечения эллипса и гиперболы.
«Точка»→«Пересечение», найдём точки пересечения эллипса и гиперболы.
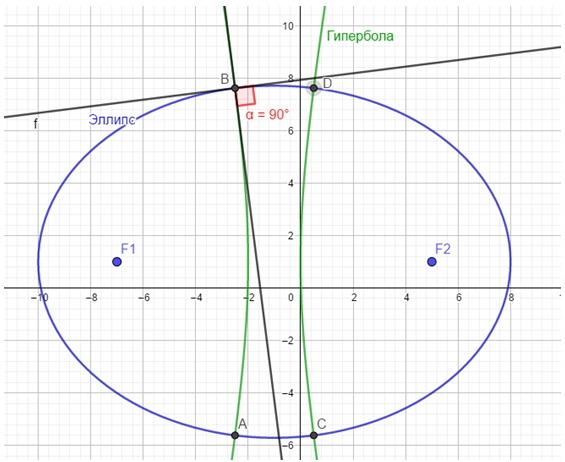
Результат выполнения шагов 1-7 представлен на рисунке 3.
Рис. 3 – Результат выполнения шагов 1-7
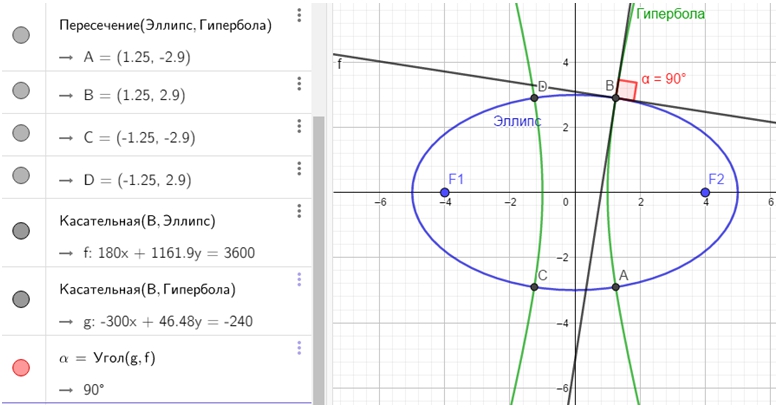
Перейдём к построению касательных к кривым и нахождению угла между ними.
Шаг 8. С помощью инструмента ![]() «Касательная», построим касательную к эллипсу в одной из точек пересечения эллипса и гиперболы. Например, в точке B.
«Касательная», построим касательную к эллипсу в одной из точек пересечения эллипса и гиперболы. Например, в точке B.
Шаг 9. С помощью инструмента ![]() «Касательная», построим касательную к гиперболе также в точке B.
«Касательная», построим касательную к гиперболе также в точке B.
Шаг 10. С помощью инструмента ![]() «Угол», найдём угол между построенными касательными.
«Угол», найдём угол между построенными касательными.
Результат выполнения шагов 1-10 представлен на рисунке 4.
Рис. 4 – Результат выполнения шагов 1-10
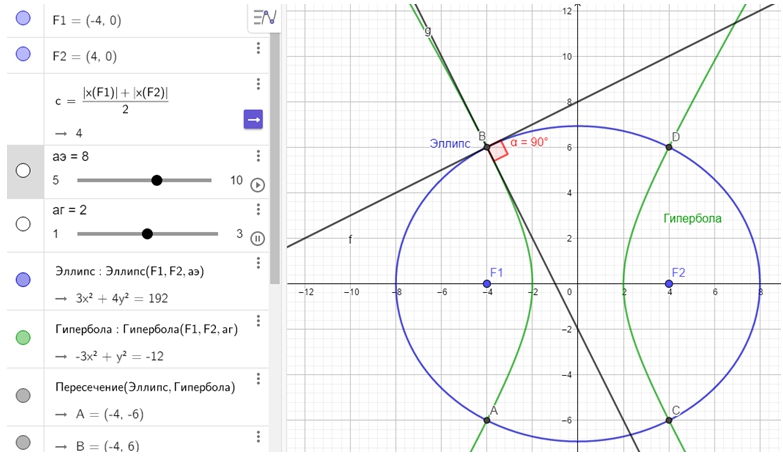
Шаг 11. С помощью инструмента «Бегунок» будем менять значения параметров аэ и аг. Формы эллипса и гиперболы будут изменяться, но угол между ними будет оставаться прямым. Один из примеров приведён на рисунке 5.Рис. 5 – Пример изменения значения параметров аэ и аг
Шаг 12. Поменяем фокусы, сместив центры кривых. Как видно из рисунка, угол между эллипсом и гиперболой также останется прямым.Рис. 6 – Угол между эллипсом и гиперболой
Поскольку параметры были выбраны произвольно, то полученный динамически результат доказывает, что любые эллипс и гипербола из семейства софокусных коник пересекаются под прямым углом.
ВыводыИспользование динамических чертежей математического пакета GeoGebra позволяет значительно упростить рассмотрение сложных задач аналитической геометрии, требующих большой визуализации, а также расширить спектр рассматриваемых задач. Кроме того, наглядность полученного с помощью пакета GeoGebra результата способствует глубокому усвоению и пониманию геометрических основ физических явлений. А, следовательно, и более простому их дальнейшему использованию в инженерных расчётах.
Данный материал может быть использован на семинарских и факультативных занятиях со студентами, для организации самостоятельной научно-исследовательской деятельности учащихся или дистанционного обучения.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Акопян А.В. Геометрические свойства кривых второго порядка / А.В. Акопян, А.А. Заславский. – М.:МЦНМО, 2007. -136с.
- Безумова О.Л. Обучение геометрии с использованием возможностей GeoGebra/ Безумова О.Л., Овчинникова Р.П. и др. Архангельск, Изд. ООО «Кира», 2011. – 140 с.
- Есаян А.Р. Преобразования объектов в GeoGebra / А.Р. Есаян, Н.М. Добровольский // Чебышевский сб., 2017. Т.18, вып.2. С.129-143.
- Есаян А.Р. Динамическая образовательная среда GeoGebra / А.Р. Есаян, Н.М. Добровольский, Е.А. Седова, А.В. Якушин– Тула: Извд-во Тул.гос.пед.ун-та им. Л.Н.Толстого, 2017. – Ч.1. – 417 с.
- Есаян А.Р. Экспериментальное обоснование гипотез в GeoGebra / А.Р. Есаян, А.В. Якушин // Чебышевский сб., 2017. Т.18, вып.1. С.92-108.
- Заславский А.А. Геометрические преобразования / А.А. Заславский. М.: МЦМНО, 2004. – 86 с.
- Краснов М.Л. Вся высшая математика: Учебник. Т. 1. Изд.4-е / М.Л. Краснов, А.И. Киселев, Г.И Макаренко и др. – М. Едиториал УРСС, 2012. – 336 с.
- Ларин С.В. Методика обучения математике: Компьютерная анимация в среде GeoGebra: учебное пособие для вузов / С.В. Ларин. – М.Издательство Юрайт, 2018. – 233 с.
- Лубягина Е.Н. Опыт организации учебно-исследовательской деятельности студентов при изучении кривых второго порядка / Е.Н. Лубягина, Л.В. Тимшина // Вестник Сыктывкарсого университета. Серия 1: Математика. Механика. Информатика. – 2017. – № 2 (23). – С. 71-84.
- Постников М.М. Аналитическая геометрия / М.М. Постников. – М.: «Наука», 1973. – 754с.
- Смирнов В.А. Геометрия с GeoGebra. Планиметрия / В.А. Смирнов, И.М. Смирнова. – М.: «Прометей», 2018. – 206с.
- Смирнов В.А. Геометрия с GeoGebra. Стереометрия / В.А. Смирнов, И.М. Смирнова. – М.: «Прометей», 2018. – 172с.
- Чеботарева Э.В. Компьютерный эксперимент с GeoGebra / Э.В. Чеботарева. – Казань: Казанский ун-т, 2015. – 61 с.
- GeoGebra Manual. The official manual of GeoGebra. PDF generated. – 325p.
Список литературы на английском языке / References in English
- Akopyan A.V. Geometricheskie svojstva krivy`x vtorogo poryadka [Geometric properties of second-order curves] / A.V. Akopyan, A.A. Zaslavskii. – M.:MCNMO, 2007. -136p. [in Russian]
- Bezumova O.L. Obuchenie geometrii s ispol`zovaniem vozmozhnostej GeoGebra [Teaching geometry using GeoGebra] / Bezumova O.L., Ovchinnikova R.P. et al. Arxangel`sk, Publishing house OOO «Kira», 2011. – 140 p. [in Russian]
- Yesayan A.R. Preobrazovaniya ob``ektov v GeoGebra / A.R. Yesayan, N.M. Dobrovolskii [Object transformations in GeoGebra] // Cheby`shevskij sb., 2017. V.18, vyp.2. p.129-143. [in Russian]
- Yesayan A.R. Dinamicheskaya obrazovatel`naya sreda GeoGebra [GeoGebra, the dynamic educational environment] / A.R. Yesayan, N.M. Dobrovolskii, E.A. Sedova, A.V. Yakushin. – Tula: Izvd-vo Tul.gos.ped.un-ta im. L.N.Tolstogo, 2017. – Issue1. – 417 p. [in Russian]
- Yesayan A.R. E`ksperimental`noe obosnovanie gipotez v GeoGebra [Experimental justification of hypotheses in GeoGebra] / A.R. Yesayan, A.V. Yakushin. // Cheby`shevskij sb., 2017. V.18, vyp.1. p.92-108. [in Russian]
- Zaslavskii A.A. Geometricheskie preobrazovaniya [Geometric transformations] / A.A. Zaslavskii. – M.: MCzMNO, 2004. – 86 p. [in Russian]
- Krasnov M.L. Vsya vy`sshaya matematika: Uchebnik. V. 1. Ed.4 [All the further mathematics: Textbook. Vol. 1. Ed. 4th] / M.L. Krasnov, A.I. Kiselev, G.I Makarenko, E.V Shikin, V.I. Zalyapin, S.K. Sobolev. – M. Editorial URSS, 2012. – 336 p. [in Russian]
- Larin S.V. Metodika obucheniya matematike: Komp`yuternaya animaciya v srede GeoGebra: uchebnoe posobie dlya vuzov [Mathematics teaching method: Computer animation in the GeoGebra environment: a textbook for universities] / S.V Larin. . – M. Publishing house Yurajt, 2018. – 233 p. [in Russian]
- Lubyagina E.N. Opy`t organizacii uchebno-issledovatel`skoj deyatel`nosti studentov pri izuchenii krivy`x vtorogo poryadka [Experience in organizing educational and research activities of students in the study of second-order curves] / E.N. Lubyagina, L.V. Timshina // Vestnik Sy`kty`vkarsogo universiteta. Seriya 1: Matematika. Mexanika. Informatika. – 2017. - № 2 (23). – p. 71-84. [in Russian]
- Postnikov M.M. Analiticheskaya geometriya [Analytical geometry] / M.M. Postnikov. – M.: «Nauka», 1973. – 754p. [in Russian]
- Smirnov V.A. Geometriya s GeoGebra. Planimetriya [Geometry with GeoGebra. Planimetry] / V.A. Smirnov, I.M. Smirnova. – M.: «Prometej», 2018. – 206 p. [in Russian]
- Smirnov V.A. Geometriya s GeoGebra. Stereometriya [Geometry with GeoGebra. Stereometry] / V.A. Smirnov, I.M. Smirnova. – M.: «Prometej», 2018. – 172 p. [in Russian]
- Chebotareva E.V. Komp`yuterny`j e`ksperiment s GeoGebra [Computer experiment with GeoGebra] / E`.V. Chebotareva. – Kazan`: Kazanskij un-t, 2015. – 61 p. [in Russian]
- GeoGebra Manual. The official manual of GeoGebra. PDF generated. – 325p.