МИНИМАЛЬНЫЕ И МАКСИМАЛЬНЫЕ ЗНАЧЕНИЯ УПРУГИХ МОДУЛЕЙ И КОЭФФИЦИЕНТА ПУАССОНА МОНОКРИСТАЛЛОВ TiFe И TiNi С ЭФФЕКТОМ ПАМЯТИ ФОРМЫ

DOI: https://doi.org/ 10.23670/IRJ.2018.75.9.006

МИНИМАЛЬНЫЕ И МАКСИМАЛЬНЫЕ ЗНАЧЕНИЯ УПРУГИХ МОДУЛЕЙ И КОЭФФИЦИЕНТА ПУАССОНА МОНОКРИСТАЛЛОВ TiFe И TiNi С ЭФФЕКТОМ ПАМЯТИ ФОРМЫ

Научная статья

Муслов С.А.*

Московский Государственный Медико-Стоматологический Университет им. А.И. Евдокимова Минздрава РФ, Москва, Россия

* Корреспондирующий автор (muslov[at]mail.ru)

Аннотация

Среди макроскопических характеристик твердых тел упругие свойства играют важнейшую роль в анализе потери устойчивости кристаллической решетки материалов к фазовым переходам. При переходах сдвигового типа, каковыми являются мартенситные превращения в металлах и сплавах, особое значение имеет исследование анизотропии параметров кристаллических структур: упругих модулей и постоянных, коэффициента Пуассона и других. В работе построены поверхности модулей Юнга и сдвига кристаллов, а также коэффициента Пуассона и их центральные сечения. Рассчитаны экстремальные значения модулей и коэффициента Пуассона кристаллов. Трансформация поверхностей и их центральных сечений дана в контексте потери стабильности сплавов к мартенситным превращениям.

Ключевые слова: модули упругости, коэффициент Пуассона, анизотропия, сплавы с памятью формы.

EXTREME VALUES OF ELASTIC MODULI AND POISSON'S RATIO OF TiFe AND TiNi WITH SHAPE MEMORY

Research article

Muslov S.A.*

Evdokimov Moscow State Medical Stomatological University, Moscow, Russia

* Corresponding author (muslov[at]mail.ru)

Abstract

Among the macroscopic characteristics of solids, elastic properties play a crucial role in the analysis of the loss of stability of the crystal lattice of materials to phase transitions. For shear-type transitions, such as martensitic transformations in metals and alloys, the study of the anisotropy of the parameters of crystal structures: elastic moduli and constants, Poisson's ratio, and others is of particular importance. In this paper, the surfaces of Young's and shear moduli of crystals, as well as the Poisson's ratio and their central sections are constructed. Extreme values of the moduli and the Poisson's ratio of the crystals are calculated. Transformation of surfaces and their central sections is given in the context of loss of stability of alloys to martensitic transformations.

Keywords: moduli of elasticity, Poisson's ratio, anisotropy, alloys with shape memory.

В В2-соединении TiFe изоморфной высокотемпературной модификации никелида титана не происходит мартенситных превращений при охлаждении, по крайней мере, до 4,2 К [1]. В сплавах же на основе TiNi хорошо изучено, что высокотемпературная ОЦК В2-фаза, упорядоченная по типу CsCl, может подвергаться при понижении температуры мартенситным превращениям по двум каналам: В2→В19' и В2→R→В19′, в зависимости от состава и термомеханической обработки, здесь В19′ и R – моноклинная и ромбоэдрическая фазы, соответственно [2]. Сверхэластичные сплавы с эффектом памяти формы нашли широкое применение в технике и медицине, например в качестве соединений в работе конструкций, имплантируемых в организм длительно функционирующих материалов, ортодонтических дуг, сосудистых стентов и сфера применения этих материалов постоянно продолжает расширяться [3]. Они способны обратимо изменять свою форму при изменении температуры, биосовместимы, проявляют высокие эластичные свойства, не разрушаются в условиях знакопеременной нагрузки, поэтому представляет интерес отдельное сравнительное исследование наиболее информативных характеристик данных интерметаллидов – упругих свойств монокристаллов.

Данные свойства действительно являются наиболее важными физико-механическими свойствами в контексте устойчивости кристаллической решетки сплавов и их предрасположенности к различным структурным и мартенситным превращениям. Монокристаллы системы TiNi-TiFe были получены методом Бриджмена в графитовых тиглях в атмосфере азота. Упругие постоянные второго порядка кристаллов были измерены резонансным методом [4], [5], [6].

Упругие постоянные c_ij и коэффициенты податливости s_ij кристаллической решетки сплавов представлены в таблице 1.

Таблица 1 – Упругие постоянные (ГПа) и коэффициенты податливости (ГПа^-1) монокристаллов

Сплав	c11	c12	c44	C'	s11	s12	s44
Ti49Ni51	164.5	133.5	33	15.5	0.022278	-0.00998	0.030303
Ti50Fe50	309	104	69	102.5	0.003897	-0.00098	0.014493

В линейном приближении упругие свойства кубических кристаллов полностью описываются матрицей, которая содержит три независимые упругие постоянные с₁₁, с₁₂ и с₄₄. Из них только постоянная с₄₄ имеет прямой физический смысл как мера сопротивления кристалла сдвигу в плоскости куба {100} вдоль любого направления <0kl>, лежащего в этой плоскости. Коэффициенты матрицы с₁₁ и с₁₂ такого простого объяснения не имеют. Однако их линейные комбинации  являются, в первом случае, мерой сопротивления кристаллов гидростатическому сжатию (модуль объемной упругости) и, во втором случае, мерой сопротивления кристалла сдвигу в плоскости {110} в направлении . При этом, с₄₄ и  – экстремальные – всегда наибольший и наименьший (или наоборот) – модули сдвига в кубическом кристалле.

Знание упругих постоянных решетки позволяет вычислить другие параметры упругости. Среди них часто используются такие как: коэффициент анизотропии , параметр анизотропии , фактор анизотропии A'=Δ/s₁₁ и экстремальные значения модуля Юнга E и сдвига G.

Экстремальные значения упругих модулей могут быть рассчитаны по формулам

                                             (1)

                                                  (2)

Как видно, какая экстремальная величина модуля Юнга является максимальной или минимальной зависит от знака и величины параметра анизотропии Δ. Экстремальные значения модулей упругости TiNi и TiFe представлены в таблице 2.

Таблица 2 – Экстремальные значения модулей упругости и их отношения

 

Аналогичные выводы можно сделать на основе анализа характеристик анизотропии сплавов (табл. 3).

Таблица 3 – Характеристики анизотропии сплавов

В качестве характеристик анизотропии можно рассматривать и значения E_max/E_min и G_max/G_min из табл. 2.

Коэффициент Пуассона (µ) является также весьма информативной характеристикой при анализе упругого поведения твердых тел. Он называется коэффициентом поперечной деформации и изначально определяется как отношение поперечной деформации к продольной, взятое с обратным знаком: .

Мы рассчитали значения коэффициента Пуассона вдоль главных направлений растяжения-сжатия и поперечной деформации. Они же являются экстремальными значениями µ (табл. 4).

Таблица 4 – Изменчивость коэффициента Пуассона

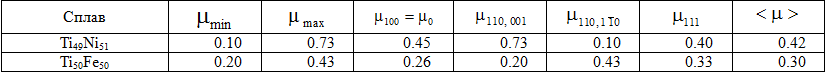
В нашем исследовании значения коэффициента Пуассона вдоль симметричных направлений определялись упругими константами кристалла по формулам

                             (3)

При этом экстремальные значения коэффициента Пуассона TiNi были рассчитаны по формулам [7] для кубических кристаллов:

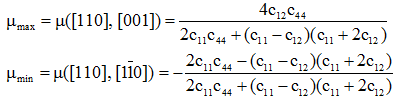 .                                                          (4)

Для TiFe правые части (4) нужно было поменять местами в силу обратной анизотропии. Усредненный по поперечным направлениям коэффициент Пуассона <μ> в табл. 4 вычисляли как [7]

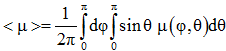                                                                              (5)

где  – коэффициент Пуассона как функция 2-х углов.

Как видно, коэффициент Пуассона никелида титана рассчитанный по данным, полученных на монокристаллах, выше, чем табличные значения для поликристаллического TiNi (0,32-0,33), которые можно встретить в литературе, например в [8]. Возможно это связано с весьма большими различиями в значениях  и в связи с этим большой погрешностью усреднения. Однако и согласно данным http://progs.coudert.name/elate/mp?query=mp-571 усредненный коэффициент Пуассона кристаллов TiNi выше упомянутых 0,32-0,33.

Что касается TiFe экстремальные значения µ из табл. 4 весьма близки к литературным данным, например размещенным на http://progs.coudert.name/elate/mp?query=mp-305: , соответственно. Среднее значение коэффициента Пуассона TiFe также очень близко к данным, полученным с помощью известных методов усреднения: µ(Voight)=0,28; µ(Reuss)=0,30; µ(Hill)=0,29 (там же).

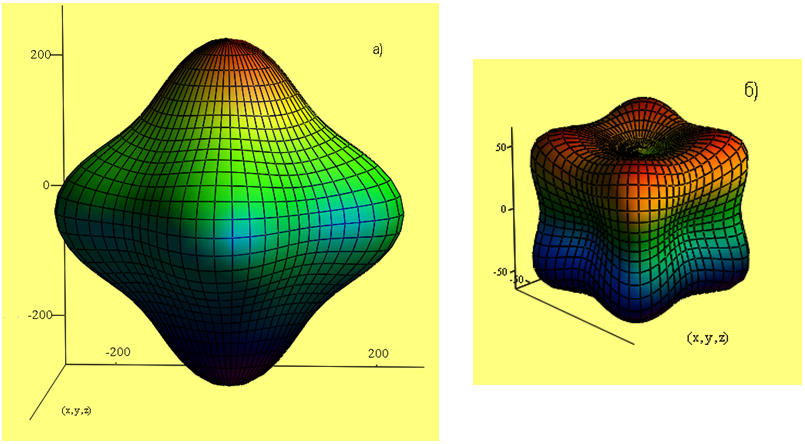
Рис. 1 – Поверхности модуля Юнга E TiFe (а) и TiNi (б) (построенные с помощью системы компьютерной алгебры Mathcad)

Обращает на себя внимание максимальное значение коэффициента Пуассона TiNi =0,73. Как видно оно больше 0,5 и выходит за пределы 0-0,5 для “обычных” материалов. Однако это не противоречит данным, например [9], согласно которым для ряда кристаллов абсолютные экстремумы коэффициента Пуассона могут превышать стандартные значения, равные −1 для стандартного минимума, и +2 для стандартного максимума.

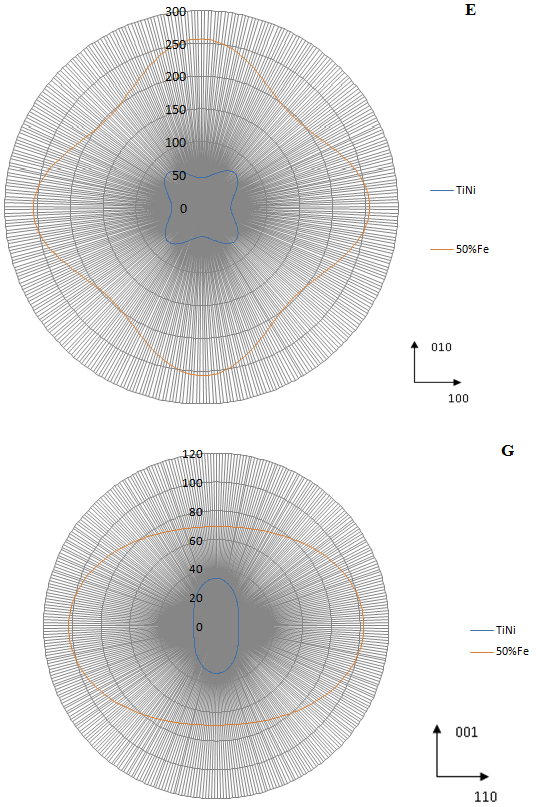
Рис. 2 – Центральные сечения указательных поверхностей модуля Юнга E (100) и сдвига G₁₁₀ монокристаллов (ГПа) TiNi и TiFe

Упругие свойства кристаллов полностью нельзя представить одной поверхностью (рис. 1) и тем более её сечениями (рис. 2). Практически полезна поверхность, изображающая изменение модуля Юнга  с направлением растяжения-сжатия в пространстве. В этом случае указательная поверхность дает полное представление только об анизотропии модуля нормальной упругости Юнга и – модуля сдвига с направлением сдвига. В последнем случае необходимо фиксировать плоскость, которая сдвигается, например {110}. При построении указательной поверхности коэффициента Пуассона можно зафиксировать положение оси растяжения-сжатия, изменяя направление поперечной деформации или наоборот.

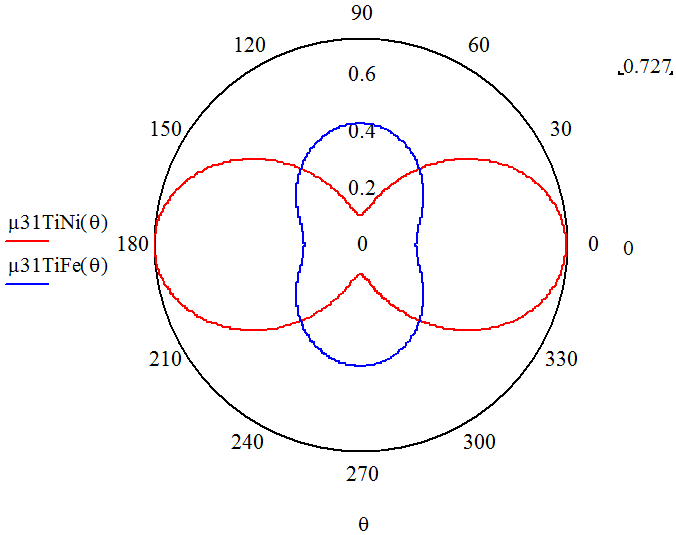
Рис. 3 – Коэффициент Пуассона  TiNi и TiFe в сравнении

Были получены срезы изоповерхностей коэффициентов Пуассона кристаллов TiNi и TiFe. Экстремумы коэффициента Пуассона в кубических кристаллах могут проявляться при растяжении в направлениях [100], [110] и [111]. Ориентационную зависимость  можно строить только для случая [110]. В двух других случаях коэффициент Пуассона будет постоянной величиной: в 1-м случае , в 3-м –  . Сечения указательных поверхностей коэффициентов Пуассона интерметаллидов TiNi и TiFe имеют вид как на рис. 3. Коэффициенты Пуассона µ(θ) вычислялись из соотношений:

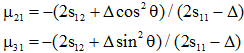 .                                                                      (6)

Как видно из приведенных таблиц вычислений и рисунков уровень упругих свойств TiNi и TiFe сплавов кардинально отличается друг от друга. Это же справедливо и для типа анизотропии интерметаллидов. Видно для TiNi в отличие от Ti₅₀Fe₅₀, модули Юнга вдоль высокосимметричных направлений подчиняются неравенству . У Ti₅₀Fe₅₀ наоборот  (отрицательная анизотропия). Кроме того параметр анизотропии Δ для Ti₅₀Fe₅₀ по знаку противоположен соответствующему параметру для монокристаллов никелида титана, что полностью соответствует графикам на рис. 1 и рис. 2 и также свидетельствует об отрицательной упругой анизотропии кристаллической структуры сплава Ti-50% Fe. Кристаллическая решетка в этом случае более податлива к сдвигу в базовой плоскости {100}, чем к “зинеровскому” сдвигу {110}<110>, играющему большую роль при мартенситной перестройке решетки в сплавах на основе никелида титана [10].

Полученные данные  и установленные различия в уровне и характере упругих свойств соединениях будут полезны для анализа механизмов и природы мартенситных превращений в сплавах никелида титана, лежащих в основе эффектов памяти формы и сверхэластичности в TiNi.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Муслов С.А. Предмартенситные состояния в монокристаллах сплавов TiNi-TiFe и TiNi-TiCu: (01.04.07): Дис. на соиск. учен. степ. канд. физ.-мат. наук / Том. гос. ун-т им. В. В. Куйбышева, 1987. - 166 с.
2. Хачин В.Н. Никелид титана. Структура и свойства / Хачин В.Н., Пушин В.Г., Кондратьев В.В. // М.: Наука, 1992. – 160 с.
3. Муслов С.А. Применение материалов с эффектом памяти формы в науке, технике и медицине. – М.: Издательский дом "Фолиум", 2007. – 328 С.
4. Кузнецов А.В. Упругие постоянные TiNi вблизи мартенситных превращений / Кузнецов А.В., Муслов С.А., Лотков А.И. и др. // Известия вузов, сер. Физика. – 1987, № 7. – С. 98-99.
5. Муслов С.А. Аномалии упругих постоянных монокристаллов Ti₅₀Ni₄₈Fe₂ вблизи мартенситных превращений / Муслов С.А., Кузнецов А.В., Хачин В.Н. и др. // Известия вузов, сер. Физика. – 1987, № 8. – С. 104-105.
6. Пушин В.Г. Микроструктура и физические свойства сплавов системы Ti₅₀Ni_50-xFe_x с эффектами памяти формы. Сообщение II. Упругие свойства / Пушин В.Г., Хачин В.Н., Юрченко Л.И. и др. // Физ. метал. и металловедение. – 1995. – Т. 79. Вып. 4. – С. 70-76.
7. Муслов С.А. Сплавы с памятью формы: свойства, получение и применение в технике и медицине / Муслов С.А., Шеляков А.В., Андреев В.А. // Москва, МГМСУ, 2018. В печати.
8. Duering T.W. Materials properties handbook: titanium alloys / Duering T.W., Pelton A.R. // Materials Park, OH: ASM International, The Materials Information Society, 1994.
9. Епишин А.И. Экстремальные значения коэффициента Пуассона кубических кристаллов / А.И. Епишин, Д.С. Лисовенко. Журнал технической физики, 2016, том 86, вып. 10. - С. 74-82.
10. De Fontaine D. Mechanical instabilities in the b.c.c. lattice and the beta to omega phase transformation // Acta met. –1970. – V. 18. – N 2. – P. 275-279.

Список литературы на английском языке / References in English

1. Muslov S.A. Predmartensitnye sostoyaniya v monokristallakh splavov TiNi-TiFe i TiNi-TiCu: (01.04.07) [Pre-martensitic States in Single Crystals of TiNi-TiFe and TiNi-TiCu Alloys]: dis. … of PhD in Physics and Mathematics / Tomsk State Un. named after V.V. Kuibyshev, 1987. - 166 p. [in Russian]
2. Hachin V.N. Nikelid titana. Struktura i svoistva. [Titanium Nickelide . Structure and Properties] / Hachin V.N., Pushin V.G., Kondratiev V.V. // M.: Nauka, 1992. – 160 p. [in Russian]
3. Muslov S.A. Primenenie materialov s effektom pamiati formy v nauke, tekhnike i mediysine [Application of Materials with Shape Memory Effect in Science, Technology and Medicine]. – M.: Publishing house “Folium,” 2007. - 328 p. [in Russian]
4. Kuznetsov A.V. Uprugie postoyannye TiNi vblizi martensitnykh prevrashhenii [Elastic Constants of TiNi near Martensitic Tansformations] / Kuznetsov A.V., Muslov S.A., Lotkov A.I. and others // Trudy vysshikh uchebnykh zavedeniy, seriya fiziki [Proceedings of Higher Educational Institutions, Physics Series]. – 1987, No. 7. – P. 98-99. [in Russian]
5. Muslov S.A. Anomalii uprugikh postoyannykh monokristallov Ti50Ni48Fe2 vblizi martensitnykh prevrashhenii [Anomalies of Elastic Constants of Ti50Ni48Fe2 Single Crystals near Martensitic Transformations] / Muslov S.A., Kuznetsov A.V., Hachin V.N. and others // Trudy vysshikh uchebnykh zavedeniy, seriya fiziki [Proceedings of Higher Educational Institutions, Physics Series] – 1987, No. 8. – P. 104-105. [in Russian]
6. Pushin V.G. Mikrostruktura i fizicheskie svoistva splavov sistemy Ti50Ni50-xFex s effektami pamiati formy [Microstructure and Physical Properties of Ti50Ni50-xFex Alloys with Shape Memory Effects] Communication II. Elastic Properties. / Pushin V.G., Hachin V.N., Yurchenko L.I. and others // Fiz. metal. i metalurgiya [Phys. Metal. and Metallurgy].- 1995. – V. 79. Issue 4. – P. 70-76. [in Russian]
7. Muslov S.A. Splavy s pamiatyu formy: svoistva, poluchenie i primenenie v tekhnike i meditsine [Alloys with Shape Memory: Properties, Production and Use in Engineering and Medicine] / Muslov S.A., Sheliakov A.V., Andreev V.A. // Moscow, MSMSU, 2018. In Press. [in Russian]
8. Duering T.W. Materials properties handbook: titanium alloys. / Duering T.W., Pelton A.R. // Materials Park, OH: ASM International, The Materials Information Society, 1994.
9. Epishin A.I. Ekstremalnye znacheniya koeffitsienta Puassona kubicheskikh kristallov [Extremal Values of Poisson's Ratio of Cubic Crystals] / A.I. Epishin, D.S. Lisovenko // Zhurnal tekhnicheskoy fiziki [Journal of Technical Physics], 2016, Vol. 86, Issue 10. – P. 74-82. [in Russian]
10. De Fontaine D. Mechanical instabilities in the b.c.c. lattice and the beta to omega phase transformation // Acta met. –1970. – V. 18. – N 2. – P. 275-279.