ХАРАКТЕРИСТИЧЕСКИЕ ПОЛИНОМЫ БУЛЕВЫХ ФУНКЦИЙ

Сдвижков О.А.

Кандидат физико-математических наук, доцент, Российский государственный университет туризма и сервиса

ХАРАКТЕРИСТИЧЕСКИЕ ПОЛИНОМЫ БУЛЕВЫХ ФУНКЦИЙ

Аннотация

Вводится понятие характеристического полинома булевой функции, имеющего заданную поляризацию переменных, и рассматривается метод представления булевой функции полиномом Рида-Маллера (каноническим поляризованным полиномом) с помощью характеристического полинома этой функции.

Доказывается, что значения характеристического полинома совпадают с соответствующими коэффициентами полинома Рида-Маллера, приводится линейный алгоритм нахождения коэффициентов полинома Рида-Маллера.

Отдельно рассматриваются положительно поляризованные характеристические полиномы и задачи, связанные с ними, включая проверку принадлежности булевой функции классу линейных функций.

Приведены примеры применения характеристических полиномов к нахождению полиномов Рида-Маллера, доопределению частичной булевой функции до линейной и проверке булевой функции на линейность.

Ключевые слова: булева функция, поляризованная переменная, суммирование по модулю 2.

Sdvizhkov O.A.

PhD in Physics and Mathematics, Associate Professor, Russian State University of Tourism and Service

CHARACTERISTIC POLYNOMIALS OF BOOLEAN FUNCTIONS

Abstract

In this article we introduce the notion of a characteristic polynomial of a Boolean function having a given polarization of variables and consider a method for representing a Boolean function by the Reed-Muller polynomial (the canonical polarized polynomial) using the characteristic polynomial of this function.

It is proved that the values of the characteristic polynomial coincide with the corresponding coefficients of the Reed-Muller polynomial and a linear algorithm for finding the coefficients of the Reed-Muller polynomial is presented.

We also consider positively polarized characteristic polynomials and problems associated with them, including checking whether the Boolean function belongs to the class of linear functions.

Examples of the application of characteristic polynomials to the determination of Reed-Muller polynomials, the extension of a partial Boolean function to a linear function and the verification of a Boolean function for linearity are given.

Keywords: Boolean function, polarized variable, modulo 2 addition.

Введение

Полиномы Рида-Маллера булевой функции  являются обобщениями полиномов Жегалкина, играющих огромную роль в построение логических схем и анализе систем булевых функций. Методы нахождения полиномов Рида-Маллера подробно рассматриваются в [7], [10], все они, следует признать, достаточно трудоемкие.

Предлагается ввести для булевой функции  понятие характеристического полинома с заданной поляризацией переменных и с его помощью находить полиномы Рида-Маллера, что значительно упрощает вычисления и решения задач, связанных с этими коэффициентами.

Следует обратить внимание на определение степени, которое применяется в статье. В нем показатель степени, чтобы не путать с булевой степенью [1, C. 24], имеет круглые скобки. Однако сказать, что это алгебраическая степень – нельзя, так как .

Приведены примеры, нахождения в Excel 2013 значений характеристического полинома, полинома Жегалкина заданной функции, проверке булевой функции на линейность и доопределения частичной булевой функции до линейной с помощью характеристического полинома и надстройки «Поиск решения» (в оригинале «Solver»).

1. Характеристические полиномы булевых функции

Следует напомнить [7], что полином булевой функции , в слагаемые которого одна часть переменных входит только с отрицаниями, а другая – только без отрицания, называется полиномом Рида-Маллера (каноническим поляризованным полиномом).

Такие полиномы обозначаются , где двоичное слово  задает поляризацию переменных, то есть показывает какие переменные входят с отрицаниями, а какие без отрицаний, значениям 0 соответствуют положительно поляризованные переменные (без отрицаний), а значениям 1 – отрицательно поляризованные переменные (с отрицаниями). Всего таких полиномов 2ⁿ.

Назовем характеристическим полиномом функции , поляризация переменных которого , полином , имеющий вид:

   (1)

где

Понятно, что каждая функция  имеет 2ⁿ характеристических полиномов. Например, при n=2 они имеют вид:

Пусть функция f задана таблица истинности:

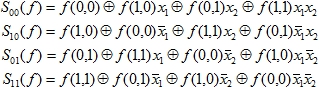
Таблица 1

  Тогда по формуле (1) получаем 8 характеристических полиномов: 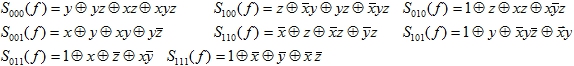Действительно, например: 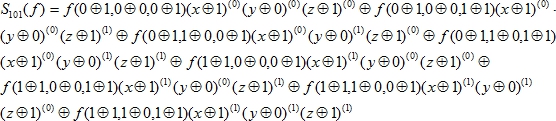Откуда следует:

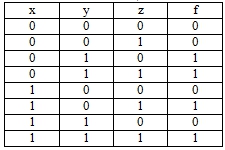
Пример 1. Найти значения полинома , полученного по таблице 1.

Открываем Excel, вводим в диапазон A1:D9 таблицу 1, затем, записывая в ячейке F2 формулу этого полинома =ОСТАТ(B2+B2*C2+A2* C2+ A2*B2*C2;2) и копируя ее в остальные ячейки диапазона F2:F9, получаем столбец значений полинома :

Рис. 1 – Значения полинома

  2. Нахождение полиномов Рида-Маллера с помощью характеристических полиномов По характеристическому полиному  можно, в свою очередь, найти характеристический полином . Теорема 1. Характеристический полином  является полиномом Рида-Маллера функции :

Доказательство сводится к доказательству истинности равенства:

   (2)

Для функций двух переменных оно истинно при всех двоичных . Например, вычисляя значения характеристического полинома

получаем: Поэтому Вычисления значений полинома  показывают, что (2) выполняется:

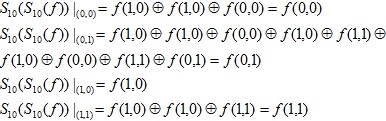
Пусть (2) истинно при n-1 переменных. Для доказательства, что оно истинно и при n переменных, воспользуемся соотношением:

Так как , из него следует:

Подстановка , если , и подстановка , если , приводит правую часть к требуемому виду.

Следствие 1. Коэффициент при конъюнкции , в полиноме  равен значению характеристического полинома  на наборе .

В силу теоремы 1, справедлив следующий алгоритм нахождения .

1. По формуле (1) находится характеристический полином .
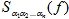2. Составляется таблица истинности полинома .
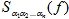3. По формуле (1) записывается полином =.

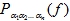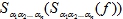Например, найдем с помощью алгоритма полином , где f задана таблицей 1.  В этом случае, как показано выше:

Составляя таблицу истинности полинома , получаем:

Таблица 2

x	y	z	S
0	0	0	1
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	0

  Применение формулы (1) дает: то есть

Следует заметить, что вычисления значений полученного полинома приводят к значениям функции f=(00110101), как и должно быть.

3. Положительно поляризованные характеристические полиномы

Полиномы , обозначаемые также P(f), являются [7, 8] положительно поляризованными полиномами – полиномами Жегалкина функций . При   формула (1) определяет положительно поляризованные характеристические полиномы:

В силу следствия 1, коэффициент при  в полиноме P(f) равен значению полинома S(f) на наборе  , то есть

  (3)

Развернутый вид этой формулы:

В частности, по значениям полинома S, показанных на рисунке 1, применяя формулу (3), получаем, что для булевой функции заданной таблицей 1 полином Жегалкина имеет вид:

На рисунке 2 показано, что значения полученного полинома совпадают со значениями функции f:

На рисунке 2 показано, что значения полученного полинома совпадают со значениями функции f:

 

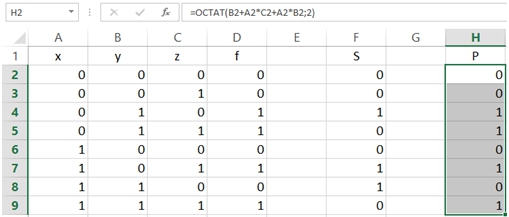
Рис. 2 – Значения полинома

  Для линейных функций, образующих замкнутый класс L [9, С. 33], выполняется:

Пример 2. Применяя характеристический полином, проверить функцию  на линейность.

1. Вводим в диапазон A1:D8 таблицу истинности и копируем ее.
2. Выделяем диапазон E9:L12, открываем контекстное меню, где выбираем опцию «Специальная вставка» и в ее диалоговом окне отмечаем «значения» и «транспонировать», что подтверждаем ОК.
3. В ячейку Е1 вводим формулу: =E$12*ЕСЛИ(E$9=1;$A1;1)*ЕСЛИ(E$10=1;$B1;1)*ЕСЛИ(E$11=1;$C1;1). Копируем ее в остальные ячейки диапазона E1:L8.
4. В ячейке М1 записываем формулу =ОСТАТ(СУММ(E1:L1);2) и копируем ее в остальные ячейки диапазона М1:М8, что возвращает в нем коэффициенты полинома Жегалкина.

 

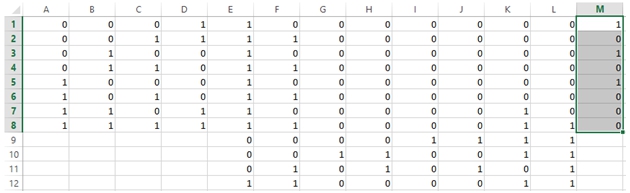
Рис. 3 – Проверка  на линейность

  Из данных диапазонов А1:С8, М1:М8 следует , то есть . Пример 3. Применяя характеристический полином, доопределить частичную булеву функцию f=(-110---0) до линейной функции. Первые четыре пункта такие же, как в предыдущем примере, только в диапазон D1:D8 (пункт 1) вместо прочерков вставляем, например, нули и считаем значения этих ячеек изменяемыми (заливаем их желтым цветом).

5. В ячейку N9 вводим формулу суммы коэффициентов полинома Жегалкина при произведениях переменных =M4+M6+M7+M8.
6. Вызываем надстройку «Поиск решения» [3, 4] и задаем сценарий поиска решения:

 

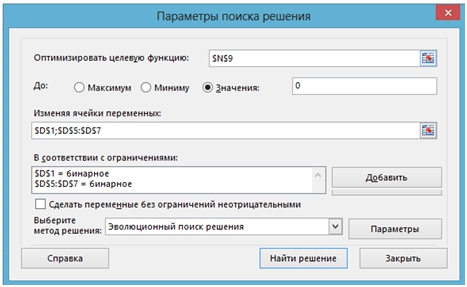
Рис. 3 – Сценарий поиска решения

 

7. Кнопка «Найти решение» возвращает сообщение «В ходе поиска невозможно улучшить текущее решение» и текущее решение, показывающее, что f=(01100110):

 

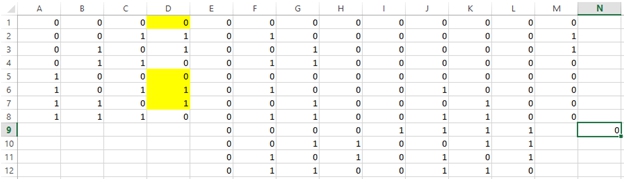
Рис. 4 – Результаты поиска решения

 

Нахождение f логическими рассуждениями приведено в [2, С. 68].

Пример 4. Проверить функцию f=(1001011010010110) на линейность

Шагами, аналогичными шагам 1 – 4 примера 2, получаем (данные диапазона F17:U21, для компактности рисунка, не приводятся), что :

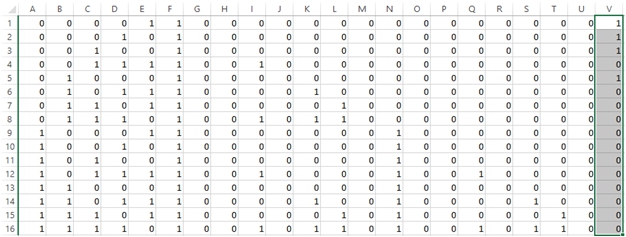
Рис. 4 – Проверка f=(1001011010010110) на линейность

 

Заключение

Приведенные примеры показывают, что характеристические полиномы позволяют достаточно просто находить коэффициенты полиномов Рида-Маллера и решать задачи, связанные с ними, особенно, пользуясь технологиями Excel. Можно пользоваться и другими информационными математическими технологиями [5, 6].

Предлагаемый метод, нахождения коэффициентов полиномов Рида-Маллера с помощью характеристических полиномов, несомненно, будет полезен при изучении полиномов Рида-Маллера и в научных исследованиях, связанных с ними.

Список литературы / References

1. Ерусалимский Я.М. Дискретная математика: теория, задачи, приложения. 3-е издание. / Я.М. Ерусалимский – М.: Вузовская книга, 2000. – 280 с.
2. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по дискретной математике: Учеб. пособие. / Г.П. Гаврилов, А.А. Сапоженко – 3-е изд., перераб. – М.: ФИЗМАТЛИТ, 2003. – 416 с.
3. Сдвижков О.А. Дискретная математика и математические методы экономики с применением VBA Excel. / О.А. Сдвижков – М.: ДМК Пресс, 2012. – 212 с.
4. Сдвижков О.А. Математика в Excel 2003. / О.А. Сдвижков – М.: СОЛОН-Пресс, 2005. – 192 с.
5. Сдвижков О.А. Математика на компьютере: Maple 8. / О.А. Сдвижков – М.: СОЛОН-Пресс, 2003. – 176 с.
6. Сдвижков О.А. MathCAD-2000. / О.А. Сдвижков – М.: Издательско-торговая корпорация «Дашков и К», 2002. – 204 с.
7. Супрун В.П. Основы теории булевых функций. / В.П. Супрун – М.: ЛЕНАНД, 2017. – 208 с.
8. Супрун В.П. Табличный метод полиномиального разложения булевых функций / В.П. Супрун // Журнал «Кибернетика», 1987, № 1. – С. 116 – 117.
9. Яблонский С.В. Введение в дискретную математику. / С.В. Яблонский – М.: Наука, 1986. – 384 с.
10. Harking B. Efficient algorithm for canonical Reed-Muller expansions of Boolean functions // IEE Proc. E, Computers and Digital Techniques. 1990. Vol. 137. №5. P. 366-370.

Список литературы на английском языке / References in English

1. Erusalimskij Ja.M. Diskretnaja matematika: teorija, zadachi, prilozhenija. 3-e izdanie [Discrete mathematics: the theory, task, appendix. 3 editions] / Ja.M. Erusalimskij – M.: Vuzovskaja kniga, 2000. – 280 p. [in Russian]
2. Gavrilov G.P., Sapozhenko A.A. Zadachi i uprazhnenija po diskretnoj matematike: Ucheb. posobie. – 3-e izd., pererab. [Tasks and exercises on discrete mathematics: studies] / G.P. Gavrilov, A.A. Sapozhenko – M.: FIZMATLIT, 2003. – 416 p. [in Russian]
3. Sdvizhkov O.A. Diskretnaja matematika i matematicheskie metody jekonomiki s primeneniem VBA Excel [Discrete mathematics and mathematical methods of economy with application VBA Excel] / O.A. Sdvizhkov – M.: DMK Press, 2012. – 212 p. [in Russian]
4. Sdvizhkov O.A. Matematika v Excel 2003 [Mathematics in Excel 2003] / O.A. Sdvizhkov – M.: SOLON-Press, 2005. – 192 p. [in Russian]
5. Sdvizhkov O.A. Matematika na komp'jutere: Maple 8 [Mathematics on the computer: Maple 8] / O.A. Sdvizhkov – M.: SOLON-Press, 2003. – 176 p. [in Russian]
6. Sdvizhkov O.A. MathCAD-2000 [MathCAD-2000] / O.A. Sdvizhkov – M.: Izdatelsko-torgovaja korporacija «Dashkov and C», 2002. – 204 p. [in Russian]
7. Suprun V.P. Osnovy teorii bulevyh funkcij [Bases of the theory Boolean functions] / V.P. Suprun – M.: LENAND, 2017. – 208 p. [in Russian]
8. Suprun V.P. Tablichnyj metod polinomial'nogo razlozhenija bulevyh funkcij [A tabulared method polynomial of decomposition Boolean functions] / V.P. Suprun // Journal « Cybernetics », 1987, № 1. – P. 116 – 117. [in Russian]
9. Jablonskij S.V. Vvedenie v diskretnuju matematiku [Introduction in discrete mathematics] / S.V. Jablonskij – M.: Science, 1986. – 384 p. [in Russian]
10. Harking B. Efficient algorithm for canonical Reed-Muller expansions of Boolean functions // IEE Proc. E, Computers and Digital Techniques. 1990. Vol. 137. №5. P. 366-370.