Наши журналы
Опубликовать статью Вход и регистрация
Расширенный поиск
Разделы статьи

ИССЛЕДОВАНИЕ ПРОГИБА ЧУВСТВИТЕЛЬНОГО ЭЛЕМЕНТА ДАТЧИКА ДАВЛЕНИЯ ПРИ ЕГО РАСПОЛОЖЕНИИ НА ТОРЦЕВОЙ СТЕНКЕ ТРУБЫ

Научная статья
Мамонова Т.Е.
DOI:
https://doi.org/10.23670/IRJ.2017.63.012
Выпуск: № 9 (63), 2017
Опубликована:
2017/09/18
PDF

Мамонова Т.Е.

ORCID: 0000-0002-8315-5424, Кандидат технических наук, Национальный исследовательский Томский политехнический университет

Работа выполнена в рамках гранта РФФИ № 16-38-00010 мол_а.

ИССЛЕДОВАНИЕ ПРОГИБА ЧУВСТВИТЕЛЬНОГО ЭЛЕМЕНТА ДАТЧИКА ДАВЛЕНИЯ ПРИ ЕГО РАСПОЛОЖЕНИИ НА ТОРЦЕВОЙ СТЕНКЕ ТРУБЫ

Аннотация

Приведена математическая модель взаимодействия трубопровода перекачки жидкости и датчика давления при его расположении на торцевой стенке трубы. Выполнена проверка адекватности приведённой математической модели «датчик давления – трубопровод». При этом использовался метод полного факторного эксперимента. Указано ранжирование параметров датчиков давления в зависимости от контактируемой среды. Исследовано влияние параметров транспортируемой жидкости и датчика давления на изменение прогиба чувствительного элемента рассматриваемого прибора с использованием уравнений регрессии. Исследование показало, что при выборе датчиков давления необходимо учитывать такие параметры датчика, как коэффициент Пуассона и толщина чувствительно элемента. Также установлено, что наибольшее влияние на прогиб чувствительного элемента датчика оказывает плотность перекачиваемой жидкости.

Ключевые слова: математическая модель, датчик давления, трубопровод, полный факторный эксперимент, адекватность модели.

Mamonova T.E.

ORCID: 0000-0002-8315-5424, PhD in Engineering, National Research Tomsk Polytechnic University

The work was carried out within the framework of the Russian Foundation for Basic Research grant No.16-38-00010 mol_a.

STUDY OF THE BEND OF THE SENSITIVE ELEMENTS OF THE PRESSURE SENSOR AT ITS LOCATION ON THE END WALL OF THE PIPE

Abstract

A mathematical model of the interaction between the liquid transporting pipeline and the pressure sensor is given for its location on the end wall of the pipe. The adequacy of the mathematical model “pressure sensor-pipeline” is checked. A full factorial experiment was used. The ranking of the pressure sensor parameters is shown depending on the medium to be contacted. The effect of the parameters of the fluid being transported and the pressure sensor on the change in the deflection of the sensing element of the device under consideration was investigated with the help of regression equations. The study showed that when selecting pressure sensors, it is necessary to take into account such parameters of the sensor as the Poisson ratio and the density of the sensitive element. It was also found that the density of the pumped liquid has the greatest influence on the deflection of the sensing element of the sensor.

Keywords: mathematical model, pressure sensor, pipeline, full factor experiment, model adequacy.

Введение

В настоящее время каждое предприятие при разработке технологических процессов применяет различные виды датчиков, средства измерения, потому что только с ними можно в полной мере получить автоматизированное производство. Частным случаем таких производств являются нефтеперерабатывающие и нефтедобывающие производства. При проектировании таких производств большое внимание уделяется выбору датчиков с целью получения достоверных и точных данных и продления их срока службы, что напрямую связано с надежностью конструкций и агрегатов трубы.

Давление наряду с такими параметрами как температура перекачиваемой жидкости, её расход и скорость является крайне важным параметром систем контроля и управления. Датчик давления состоит из первичного преобразователя давления, в составе которого чувствительный элемент является приемником давления, схемы вторичной обработки сигнала, различных по конструкции корпусных деталей, в том числе для герметичного соединения датчика с объектом и защиты от внешних воздействий и устройства вывода информационного сигнала. При проектировании важно учитывать влияние среды в трубопроводе на динамику чувствительного элемента, так как это позволит обеспечить не только необходимую точность, но и повысит надежность конструкции «датчик давления – трубопровод» и как следствие надежность системы в целом.

Таким образом, задача по получению и исследованию адекватной математической модели, связывающей динамику чувствительного элемента датчика давления и давление в трубопроводе, в настоящее время является актуальной.

Получением математической модели, позволяющей исследовать характер течения жидкости в трубе и влияние данного характера на датчики, ранее проводились в работах [1, С. 48], [2, С. 36], [3, С. 75], [4, С. 15] и [5, С. 67]

Ранее в работе [6, С. 285] автором была получена математическая модель «датчик давления – трубопровод» для случая, когда датчик расположен на торцевой стенке трубопровода (рис. 1), которая имеет вид:

25-09-2017 10-22-53   (1)

где ω – прогиб чувствительного элемента датчика, м; P0 – распределенная внешняя нагрузка, действующая на упругий элемент, Па; y0 – диаметр трубопровода, м; x0 – длина трубопровода, м; ρм– плотность мембраны, кг/м3; E – модуль Юнга, Па; h – толщина мембраны, μ – коэффициент Пуассона (отношение относительного поперечного сжатия к относительному продольному растяжению), β – коэффициент демпфирования.

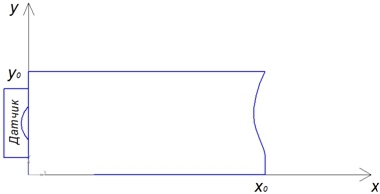
25-09-2017 10-27-59

Рис. 1 – Схема расположения датчика на трубопроводе

 

Математическая модель (1) связывает закон изменения давления рабочей среды в трубопроводе и прогиб упругого элемента датчика давления.

Было установлено, что изготовители датчиков давления в зависимости от контактируемой среды конструируют датчики с различными параметрами. Наиболее распространённые взяты из [7] и [8] и представлены ниже:

1) толщина чувствительного элемента датчиков составляет: 0,2 – 1,6 мм;

2) материал чувствительных элементов различен по плотности:

  • (7400 ÷ 7800) кг/м3 – для пьезокерамических элементов;
  • (7700 ÷ 8100) кг/м3 – для элементов из нержавеющей стали;
  • (2330 ÷ 3050) кг/м3 – для элементов из монокристаллического кремния;

3) модуль упругости элементов (модуль Юнга):

  • (78 ÷ 190) ГПа (для пьезокерамических элементов);
  • (193 ÷ 200) ГПа (для элементов из нержавеющей стали);
  • (109 ÷ 131) ГПа (для элементов из монокристаллического кремния);

4) коэффициент Пуассона зависит не от размеров тела, а от природы материала:

  • (0,29 ÷ 0,35) – для пьезокерамических элементов;
  • (0,27 ÷ 0,30) – для элементов из нержавеющей стали;
  • 0,266 – для элементов из монокристаллического кремния.

5) плотность нефти зависит от температуры, поддерживаемой в трубопроводе и от месторождений добычи ископаемого, и колеблется в диапазоне (730 ÷  1040) кг/м3.

Таким образом, на изменение прогиба чувствительного элемента  датчиков давления влияет большое количество параметров.

В табл. 1 приведены параметры датчика, трубопровода и нефти. Параметры чувствительного элемента датчика давления взяты из [7], [8], [9] и соответствуют параметрам наиболее применимых датчиков в нефтегазопромышленности. При этом установлено, что материалом чувствительного элемента датчика (мембраны) служит нержавеющая сталь 316L. Толщина мембраны взята как среднее значение по всей её длине.

 

Таблица 1 – Параметры чувствительного элемента  датчика давления, трубопровода и нефти

Название параметра Значение параметра Название параметра Значение параметра
Коэффициент Пуассона, μ 0,27 Толщина мембраны, hм 0,0012
Модуль Юнга, E (ГПа) 200 Коэффициент демпфирования, β 0,3
Плотность мембраны, ρм кг/м3 8000 Диаметр трубопровода, y0 0,5
Длина трубопровода, x0 100 Плотность нефти,  кг/м3 800
 

В данной работе выполнен эксперимент для выявления влияния параметров датчика и перекачиваемой жидкости на прогиб чувствительного элемента датчика давления. Исследуемые параметры:

  • коэффициент Пуассона ;
  • толщина чувствительно элемента h;
  • плотность нефти

Диапазон значений параметров мембраны равен диапазону возможных значений для материалов чувствительного элемента. Плотность нефти изменяется в диапазоне в зависимости от месторождений мира [10].

Влияние вариации параметров были выявлены при  использовании полного факторного эксперимента, изложенного в работах [11, С. 6] , [12], [13].

В табл. 2 представлены расчетные данные проведения полного факторного эксперимента.

 

Таблица 2 – Расчётные формулы

25-09-2017 10-30-45

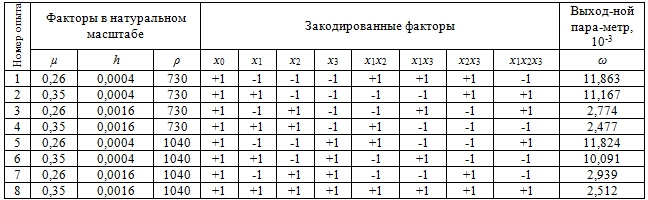
В табл. 3 приведены результаты полного факторного эксперимента для трех выбранных факторов, а также их закодированные значения.

 

Таблица 3 – Результаты полного факторного эксперимента для трех факторов

25-09-2017 10-31-02

 

Уравнение регрессии для трехфакторного эксперимента имеет общий вид:

25-09-2017 10-32-40  (1)

где bj – коэффициенты регрессии (j = (0 ÷ 3)).

Значение коэффициентов регрессии определяются по следующим формулам:

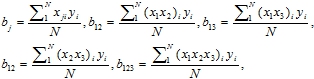25-09-2017 10-33-50  (2)

где xij - кодированные значения фактора xj в i-м опыте.

В результате обработки данных с помощью программного пакета MathCAD была получена модель зависимости прогиба чувствительного элемента датчика давления от взятых параметров в виде уравнения регрессии:

25-09-2017 10-37-38  (3)

Для проверки модели (1) на адекватность был применён критерий Фишера, в соответствии с которым:

25-09-2017 10-38-45  (4)

где 25-09-2017 10-39-46 – дисперсия адекватности, 25-09-2017 10-39-54 – табличное значение по критерию Фишера, 25-09-2017 10-40-01 – дисперсия параметра оптимизации.

Дисперсия адекватности [12]:

25-09-2017 10-42-06  (5)

где 25-09-2017 10-42-58– число степеней свободы, k – число факторов. Дисперсия параметра оптимизации [12]:

25-09-2017 10-43-32  (6)

С учетом численных значений и табличным данным, взятым из [13] получаем 25-09-2017 10-44-31. Следовательно, модель (1) адекватна.

На основании полученной модели (2) в пакете MatLab построены поверхности изменения прогиба чувствительного элемента датчика ω от  изменения коэффициент Пуассона μ, толщины чувствительно элемента h и плотности нефти ρ (рис. 2).

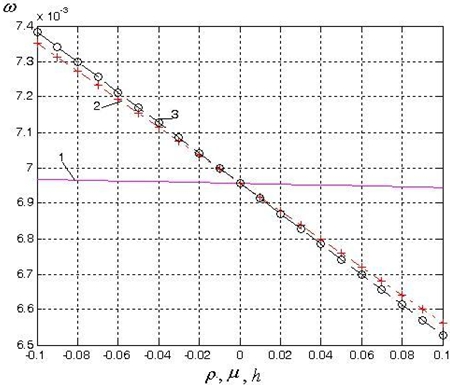
25-09-2017 10-46-13

Рис. 2 – Прогиб чувствительного элемента датчика ω  при 25-09-2017 10-47-02

Таким образом, на прогиб чувствительного элемента датчика давления при его расположении на торцевой стороне трубы оказывают влияние все рассматриваемые параметры, т.е. плотность ρ жидкости, коэффициент Пуассона  и толщины чувствительно элемента  датчика, однако по представленным графикам выявлено, что наибольшее воздействие производит плотность жидкости ρ.

Вывод

Выполненный полный факторный эксперимент доказал, что математическая модель «датчик давления – трубопровод» для случая, когда датчик расположен на торцевой стенке трубопровода, описывающая закон изменения давления рабочей среды в трубопроводе и прогиб упругого элемента датчика давления,  может использоваться в расчетах, так как данная модель является адекватной. Проведенное исследование выявило, что при проектировании трубопровода и подбора измерительной аппаратуры  необходимо учитывать не только параметры датчиков, но и диапазон изменения плотности перекачиваемой по трубопроводу жидкости.

Список литературы / References

  1. Крайнова Л.Н. Пространственные нелинейные колебания трубопровода при гармоническом возбуждении / Л. Н. Крайнова, А. И. Муницын // Машиностроение и инженерное образование. – 2010. – №  – С. 46–51.
  2. Зарипов Д. М. Математическое моделирование динамики трубопровода под действием волн давления в транспортируемой жидкости: дис. … канд. физ.-мат. наук: 05.13.18: защищена 12.11.06: утв. 10.07.07/ Д.М. Зарипов/ – Стерлитамак.  – 109 с.
  3. Смирнов Л. В., Овчинников В. Ф., Силантьева В. М. Динамика трубопровода при гидравлическом ударе в потоке транспортируемой жидкости / Л. В. Смирнов, В. Ф. Овчинников, В. М. Силантьева // Проблемы прочности и пластичности. – 2010. – № 72. – С. 73–79.
  4. Покладова Ю. В. Математическое моделирование системы «трубопровод - датчик давления»: автореферат дис.… канд. физ.-мат. наук: 05.13.18/ Ю. В. Покладова – Ульяновский государственный технический университет. – Ульяновск. 2008. – 109 с.
  5. Покладова Ю. В. Математическое моделирование динамики упругого элемента датчика давления в трубопроводе конечной длины / Ю. В. Покладова, Ю. А Решетников // Прикладная математика и механика: Сборник научных трудов. – Ульяновск: УлГТУ, 2004. – С.114-120.
  6. Мамонова Т. Е., Овчаров А. Э. Математическая модель системы «датчик – трубопровод» при расположении датчика на торцевой стенке трубы/ Т. Е. Мамонова // Сборник трудов XIII Международной научно-практической конференции студентов, аспирантов и молодых учёных «Молодёжь и современные информационные технологии». – Томск: Томский политехнический университет. – 2016. С.284–285.
  7. Пьезоэлектрические свойства пьезокерамики. [Электронный ресурс]. – URL: http://symmetron.ru/suppliers/apc/ (Дата обращения: 10.08.2017 г.)
  8. Плотность нержавеющей стали. [Электронный ресурс]. – URL: http:// www.m.-k.k.ru/plotnost-nerzhaveyuschey-stali/ (Дата обращения: 09.08.2017 г.)
  9. Тиняков Ю. Н., Милешин С. А., Андреев К. А. Анализ конструкций зарубежных прототипов датчиков давления/ Ю. Н. Тиняков // Наука и образование. – 2011. С. 1–13. [Электронный ресурс]. – URL: http://technomag.bmstu.ru/doc/219081.html (Дата обращения: 08.08.2017 г.)
  10. Плотность нефти. [Электронный ресурс]. – URL: https://goo.gl/zgQZ5f (дата обращения: 08.08.2017 г.)
  11. Кузнецова Е. В. Математическое планирование эксперимента: учебно-методическое пособие для студентов очного и заочного обучения специальностей «Технология обработки металлов давлением», «Динамика и прочность машин», «Компьютерная механика», «Компьютерная биомеханика» / Е. В. Кузнецова/ – Пермь: Перм. гос. техн. ун-т, 2011. – 35 с.
  12. Применение полного факторного эксперимента. [Электронный ресурс]. – URL: http://textarchive.ru/c-1513574.html  (Дата обращения: 18.08.2017 г.)
  13. Коэффициент Фишера. [Электронный ресурс]. – URL: http://www.studfiles.ru/preview/5856922/page:5/ (Дата обращения: 08.08.2017 г.)

Список литературы на английском языке / References in English

  1. Kraynova L. N. Prostranstvennie nelineynie kolebaniya truboprovoda pri garmonicheskom vozbuzhdenii [Spatial nonlinear fluctuations of the pipeline at harmonious excitement] / L. N. Kraynova, A. I. Municin // Mashinostroenie i ingenernoe obrazovanie [Mechanical engineering and engineering education]. – 2010. – № 2. – P. 46–51. [in Russian]
  2. Zaripov D. M. Matematicheskoe modelirovanie dinamiki truboprovoda pod deystviem voln davleniya v transportiruemoy zhidkosti [Mathematical modeling of the pipeline dynamics under the influence of pressure waves in the transported liquid]: dis. … of PhD of physical and mathematical sciences: 05.13.18: defense of the thesis 12.11.06: approved 07.07/ D. M. Zaripov – Sterlitamak. 2006. – 109 p. [in Russian]
  3. Smirnov L. V., Ovchinnikov V. F., Silantyeva V. M. Dinamika truboprovoda pri gidravlicheskom udare v potoke transportiruemoy zhidkosti [Dynamics of the pipeline at water hammer in a stream of the transported liquid] / L. V. Smirnov, V. F. Ovchinnikov, V. M. Silantyeva // Problemi pochnosti i plastichnosti [Durability and plasticity problems] – 2010. – № 72. – P. 73–79. [in Russian]
  4. Pokladova Yu. V. Matematicheskoye modelirovaniye sistemi «truboprovod – datchik davleniya» [Mathematical modeling of "the pipeline-pressure sensor" system]:  abstract of dis. … of PhD of physical and mathematical sciences: 13.18/ Yu. V. Pokladova/– Ulyanovskiy gosudarstvenniy tehnicheskiy universitet [Ulyanovsk state technical university]. – Ulyanovsk. 2008. – 109 p. [in Russian]
  5. Pokladova Yu. V. Matematicheskoye modelirovaniye dinamiki uprugogo elementa datchika davleniya v truboprovode konechnoy dlini [Mathematical modeling of dynamics of an elastic element of the pressure sensor in the pipeline of final length] / Pokladova Yu. V., Yu. A. Reshetnikov // Prikladnaya matematika i mehanika: Sbornik nauchnih trudov [Applied mathematics and mechanics: Collection of scientific works] – Ulyanovsk: UlGTU, 2004. – P.114-120. [in Russian]
  6. Mamonova T. E., Ovcharov A. E. Matematicheskaya model sistemi «datchik – truboprovod» pri raspolozhenii datchika na torcevoy stenke trubi [The mathematical model «the sensor-the pipeline» systems at a sensor arrangement on a face wall of a pipe] / T. E. Mamonova // Sbornik trudov XIII Mazhdunarodnoy nauchno-prakticheskoy konferencii studentov, aspirantov i molodih uchyonih «Molodyozh I sovremennie informacionnie tehnologii» [Collection of works XIII of the International scientific and practical conference of students, graduate students and young scientists "Youth and modern information technologies"] – Tomsk: Tomskiy politehnicheskiy universitet [Tomsk Polytechnic University]. – 2016. P. 284–285. [in Russian]
  7. Pyezoelektricheskie svoystva pyezokeramiki. [Piezoelectric properties of a pyezokeramika] [Electronic resource]. – URL: http://symmetron.ru/suppliers/apc/ (accessed: 10.08.2017 г.) [in Russian]
  8. Plotnosty nerzhaveyuschey stali [Density of stainless steel] [Electronic resource]. – URL: http:// www.m.-k.k.ru/plotnost-nerzhaveyuschey-stali/ (accessed: 09.08.2017 г.) [in Russian]
  9. Tinyakov Yu. N., Mileshin S. A., Andreev K. A. Analiz konstrukciy zarubezhnih prototipov datchikov davleniya [Analysis of foreign prototypes designs of pressure sensors] / Yu. N. Tinyakov // Nauka I obrazovaniye [Science and education] – 2011. С. 1– 13. [Electronic resource]. – URL: http://technomag.bmstu.ru/doc/219081.html (accessed: 08.08.2017 г.) [in Russian]
  10. Plotnosty nefti [Oil density] [Electronic resource]. – URL: https://goo.gl/zgQZ5f (accessed: 08.08.2017 г.) [in Russian]
  11. Kuznecova E. V. Matematicheskoe planirovaniye eksperimenta: uchebno-metodicheskoe posobie dlya studentov ochnogo I zaochnogo obucheniya specialnostey «Tehnologiya obrabotki metallov davleniem», «Dinamika I prochnost mashin», «Kompiuternaya mehanika», «Kompiuternaya biomehanika» [Mathematical planning of an experiment: an educational and methodical grant for students of a resident and correspondence course of specialties "Technology of Processing of Metals Pressure", "Dynamics and Durability of Cars", "Computer Mechanics", "Computer Biomechanics"] / E. V. Kuznecova/ – Perm: Perm. gos. tehn. un-t, 2011. – 35 с. [in Russian]
  12. Primeneniye polnogo faktornogo eksperimenta [Application of a complete factorial experiment]. [Electronic resource]. – URL: http://textarchive.ru/c-1513574.html (accessed: 18.08.2017 г.) [in Russian]
  13. Koefficient Fishera [Fischer's coefficient] [Electronic resource]. – URL: http://www.studfiles.ru/preview/5856922/page:5/ (accessed: 08.08.2017 г.) [in Russian]