ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ОСОБЕННОСТЕЙ ЭЛЕКТРОХИМИЧЕСКОГО РАСТВОРЕНИЯ ПРИ ОБРАБОТКЕ ТОЧЕЧНЫМ ЭЛЕКТРОДОМ-ИНСТРУМЕНТОМ В ПАССИВИРУЮЩЕМ ЭЛЕКТРОЛИТЕ

Шерыхалина Н.М.

ORCID: 0000-0002-2808-1311, доктор технических наук, Уфимский государственный авиационный технический университет

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (код проекта 17-07-00356)

ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ОСОБЕННОСТЕЙ ЭЛЕКТРОХИМИЧЕСКОГО РАСТВОРЕНИЯ ПРИ ОБРАБОТКЕ ТОЧЕЧНЫМ ЭЛЕКТРОДОМ-ИНСТРУМЕНТОМ В ПАССИВИРУЮЩЕМ ЭЛЕКТРОЛИТЕ

Аннотация

Процесс электрохимической обработки моделируется с помощью решения задачи Шварца для комплексного потенциала на параметрической области в виде полосы. На этой основе разработан численно-аналитический метод решения задачи, позволивший использовать для моделирования экспериментальные данные, а именно, немонотонную зависимость особого вида плотности тока от анодного потенциала. Это позволяет объяснить появление в натурном эксперименте на обрабатываемой поверхности трех зон: зоны активного растворения, зоны отсутствия растворения, соответствующей падающей части зависимости, и зоны слабого растворения, которая соответствует малым плотностям тока.

Ключевые слова: электрохимическое формообразование, анодный потенциал, немонотонная зависимость, комплексные переменные.

Sherykhalina N.M.

ORCID: 0000-0002-2808-1311, PhD in Engineering, Ufa State Aviation Technical University

The work was supported by the Russian Foundation for Basic Research (project code 17-07-00356)

NUMERICAL INVESTIGATION OF MAIN FEAURES OF ELECTROCHEMICAL DISSOLUTION AT PROCESSING BY POINT ELECTRODE-TOOL IN PASSIVE ELECTROLYTE

Abstract

The process of electrochemical processing is simulated with the help of the Schwarz solution of the complex potential in the parametric region in the form of a strip. On this basis, a numerical-analytical method for solving the problem is developed. This method allowed using experimental data, and namely, the non-monotonic dependence of a special type of current density on the anode potential. This explains the emergence of three-zones in the full-scale experiment on the treated surface: Active dissolution zones, zones of no dissolution of the corresponding falling dependence portion, weak dissolution zones corresponding to the low current densities.

Keywords: electrochemical formation, anodic potential, non-monotonic dependence, complex variables.

Рассматривается двумерная задача. На рис. 1,а показана схема межэлектродного пространства (МЭП) при электрохимической обработке (ЭХО). Проволочный электрод-инструмент (ЭИ) в. сечении представляется точкой. Поверхность анода – плоская.

Считается что электрическое поле соленоидально и потенциально. Для решения таких задач эффективно используются методы теории функций комплексного переменного. Применяется реальная зависимость потенциала анода  от плотности тока J, т.е. . Образом МЭП на плоскости комплексного потенциала  (Φ –потенциал электрического поля, Ψ – функция тока) является криволинейная полуполоса. Ширина полуполосы равна , где I – ток, протекающий в ячейке единичной толщины, κ – электропроводность электролита (рис. 1,б).

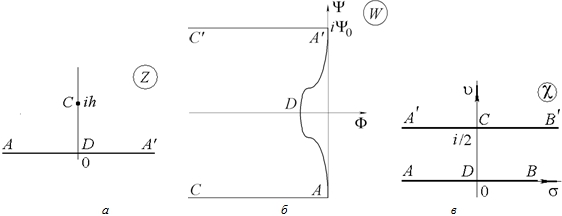
Рис. 1 – Формы области на плоскостях.

Примечание: а – физической; б – комплексного потенциала; в – параметрической.

В качестве области изменения параметрического переменного c=s+iu выбирается полоса  (рис. 1,в). Функция

   (1)

конформно отображает область плоскости c на МЭП. Производная этой функции   (2) Отображение c на W должно удовлетворять следующим условиям:      (3)    (4) Решение задачи представляется в виде суммы     (5) Здесь     (6) Производные этой функции      (7)

Функция  удовлетворяет условию (3); на . Коэффициент v1 в (5) используется для численного приведения безразмерных значений потенциала к экспериментальным. Функция  должна иметь следующие свойства: , при c=s+i/2 . Такую функцию  можно аналитически продолжить на полосу ширины, равной единице. При этом согласно принципу симметрии [1, С. 158]

   (8)

На действительной полуоси выбирается сетка . Искомыми параметрами являются значения . Поскольку  экспоненциально убывает при σ→∞, принимается , По этим значениям строится кубический сплайн S(σ), дважды непрерывно дифференцируемый, интерполирующий искомую функцию.

Функция  определяется при решении задачи Шварца. Решение дается формулой [2, С. 9]

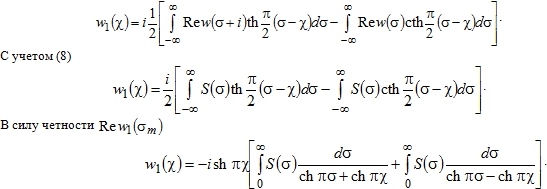
Полученные в узловых точках  значения  интерполируются кубическим сплайном P(σ), дважды непрерывно дифференцируемым. При этом коэффициенты сплайна являются значениями первой производной P'(σ_m).

Величина, комплексно сопряженная напряженности с учетом (2) и (7) определяется производной

где коэффициенты v₁ и v₂, как и в (5), используются для численного приведения безразмерных значений потенциала и плотности тока к экспериментальным.

Предполагается, что анодный потенциал зависит только от нормальной составляющей вектора плотности тока . Рассмотрим зависимость, аппроксимирующую экспериментальные результаты [3, С. 31] (рис. 2)

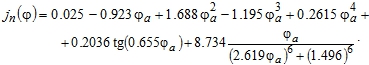  (9)

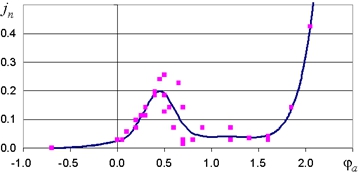
Рис. 2 – График аппроксимирующей зависимости (9) в сравнении с результатами эксперимента

 

Такая немонотонная зависимость наблюдается при обработке в пассивирующих электролитах при которой повышается локализация процесса растворения и точность копирования [3, С. 343]. Проведенные ранее исследования [4] – [7] существенно использовали монотонность этой зависимости.

Для численного решения задачи применялся метод коллокаций. Условие (9) выполнялось в узловых точках . Получалась система нелинейных уравнений, которая решалась методом Ньютона с регулированием шага. При решении задачи использовались значения , найденные эмпирически.

Заметим, что аналогичные задачи решались в [8], [9], однако при решении использовались степенные ряды, условие сходимости которых существенно ограничивает вид используемой в качестве краевого условия (4) функции. Вследствие этого в [8], [9] использовалась упрощенная зависимость, далекая от функции (9), аппроксимирующей экспериментальные данные.

Результаты решения приведены на рис. 3 – 5. На рис. 3 показано распределение потенциала по анодной поверхности, на рис. 4 – распределение тангенциальной составляющей и полной безразмерной плотности тока, на рис. 5,а  – нормальной составляющей безразмерной плотности тока.

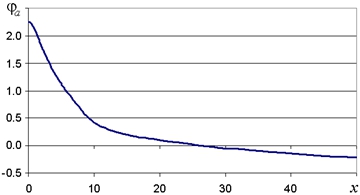
Рис. 3 – Распределение потенциала по анодной поверхности

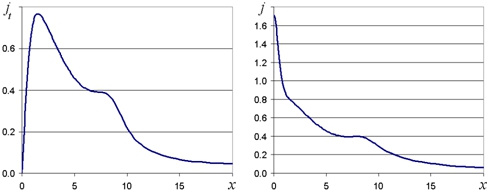
Рис. 4 – Распределение плотности тока по анодной поверхности

Примечание: а – тангенциальной составляющей; б – полной плотности тока.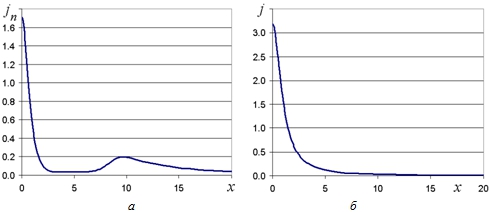  

Рис. 5 – Распределение нормальной составляющей плотности тока по анодной поверхности

Примечание: а – для зависимости (9); б – для эквипотенциального анода.  

На рис. 5,б для сравнения приведен график распределения плотности тока по анодной поверхности в условиях постоянства потенциала. Видно, что непостоянство потенциала анода приводит к значительному перераспределению нормальной составляющей плотности тока.

Перераспределение тока также проиллюстрировано на рис. 6, где показаны величины тока y, протекающего на участках анода от точки D (x=0) до точки с абсциссой x, отнесенного к , для переменного (1) и постоянного (2) анодного потенциала (  имеет смысл величины общего тока, протекающего в цепи). Как легко заметить, при постоянном потенциале анода на расстоянии 10h протекает более 90% тока, при переменном около 40%.

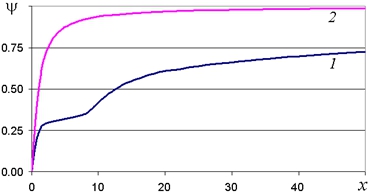
Рис. 6 – Распределение функции тока по анодной поверхности

 

Для анализа вычислительных погрешностей применялась численная фильтрация [10] зависимостей десятичного логарифма оценок погрешностей от десятичного логарифма числа точек колллокаций n (рис. 7), основанная на многокомпонентном анализе этих зависимостей и поочередном исключении (отфильтровывании) компонент погрешности. Цифрой 0 обозначены оценки результатов вычислений, цифрами 1, 2 – результаты 1-й и 2-й фильтрации. В результате оценок выяснено, что погрешность вычисленного значения потенциала при n=640 не превышает 10^-5, плотности тока 10^-4.

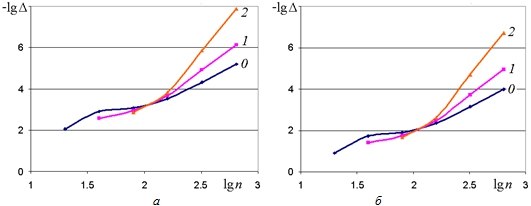
Рис. 7 – Оценка погрешности параметров в точке D

Примечание: а – потенциала; б – плотности тока  

В [3, С.347] приведена фотография поверхности, полученная при обработке сферическим ЭИ в водном растворе нитрата натрия. Анализ образца показал, что на его поверхности образовались 3 характерные зоны, находящиеся в области различных значений анодного потенциала и плотностей тока. Зона 1 активного растворения располагается вблизи оси ЭИ, где поверхность катода находилась на малом расстоянии от поверхности анода. Плотность тока для этой зоны максимальна. Зона 2 соответствует области пассивного состояния поверхности, о чем свидетельствует отсутствие на ней следов электрохимического растворения. И, наконец, зона 3 соответствует области слабого анодного растворения.

Из сопоставления зависимости (9) (см. рис.2), кривых распределения плотностей тока по координате (рис. 5) и результатов эксперимента можно предположить, что зона 2, где железо находилось в пассивном состоянии и отсутствовало растворение, соответствует падающей части характеристики (9). Зона 1, где протекали процессы активного электрохимического растворения, соответствует возрастающей части характеристики, находящейся за зоной пассивации. Зона 3 соответствует малым плотностям тока в возрастающей части характеристики (9).

Таким образом, в данной работе предложен численно-аналитический метод, включающий решение задачи Шварца. С помощью этого метода удалось использовать зависимость нормальной составляющей плотности тока от анодного потенциала, полученную путем аппроксимации экспериментальных данных. Это было невозможно при применении известных ранее методов, основанных на разложении в ряды, поскольку реальная зависимость содержит круто падающие и возрастающие участки.

С помощью разработанного метода были рассчитаны распределения потенциала и составляющих плотности тока на поверхности анода, которые невозможно получить в натурном эксперименте.

Список литературы / References

1. Лаврентьев М. А. Методы теории функций комплексного переменного / М. А. Лаврентьев, Б. В. Шабат. – М.: Наука. – 1987. – 688 с.
2. Терентьев А. Г. К линейной теории кавитационного обтекания препятствий / А. Г. Терентьев // Сборник научных трудов «Вопр. прикл. матем. и мех.». Чебоксары: изд-во Чуваш. ун-та. – 1971. – Вып.1. – С. 3–35.
3. Житников В. П. Импульсная электрохимическая размерная обработка. / В. П. Житников, А. Н. Зайцев. – М.: Машиностроение. –2008. – 413c.
4. Клоков В. В. Стационарное анодное формообразование двугранным катодом при неравномерной поляризации анода / В. В. Клоков, С. Е. Шишкин // Сборник научных трудов «Тр. семин. по краевым задачам». – Казань: Казанск. ун-т. – 1985. – Вып. 22. – С. 117-124.
5. Каримов А. Х. Методы расчета электрохимического формообразования / А. Х. Каримов, В. В. Клоков, Е. И. Филатов – Казань: Казанск. ун-т. – 1990. – 387 с.
6. Газизов Е. Р. Анодное формообразование двугранным катодом при неравномерной поляризации анода / Е. Р. Газизов, Д. В. Маклаков // Известия вузов. Авиационная техника. – 2002. – №4. – С. 55–57.
7. Газизов Е. Р. Анодное формообразование криволинейным катодом при неравномерной поляризации анода / Е. Р. Газизов // Известия КГАСУ. – Казань. – 2006. – №1(5). – С. 132–135.
8. Муксимова Р. Р. Исследование влияния неравномерности потенциала при электрохимической обработке в пассивирующем электролите / Р. Р. Муксимова, В. П. Житников, А. А. Зарипов // Материалы III Междунар. науч.-практ. конф. «Теория и практика современных электрохимических производств». СПб. – 2014. – C. 37–38.
9. Зарипов А. А. Моделирование электрохимической обработки стержневым электрод-инструментом в пассивирующем электролите // Сборник научных трудов по материалам VIII Международной научно-практической конференции «Теоретические и прикладные аспекты современной науки». – Часть 1. – Белгород. – 2015. – С. 8 – 14.
10. Житников В. П. Применение многократной фильтрации при численном решении задач методами теории функций комплексного переменного / В. П. Житников, Н. М. Шерыхалина // Вычислительные технологии. – 2013. – Т. 18. – №1. – С. 15–24.

Список литературы на английском языке / References in English

1. Lavretiev M. A. Metody teorii funktsiy kompleksnogo peremennogo [The methods of the theory of functions of complex variable] / M. A. Lavretiev, B. V. Shabat // – Moscow: Nauka. – 1987. – 688 p. [in Russian]
2. Terentiev A. G. K lineynoy teorii kavitatsionnogo obyekaniya prepyatstviy [On the linear theory of cavitating flows about obstacles] / A. G. Terentiev // Sbornik nauchnyh trudov “Voprosy prikladnoy matematiki i mekhaniki” [Collection of scientific works “Problems of applied Mathematics and mechaniks”]. – 1971. – V. 1. – Cheboksary: Chuvash University. – P. 3–35. [in Russian]
3. Zhitnikov V. P. Impulsnaya electrohimicheskaya razmernaya obrabotka [Impulse electrochemical dimensional machining] / V. P. Zhitnikov, A. N. Zaytsev // – Moscow: Mashinostroenie. – 2008. –413 p. [in Russian]
4. Klokov V. V. Statsionarnoye anodnoye formoobrazovanie dvugrannym katodom pri neravnomernoy plyarizatsii anoda [Stationary anodic shaping by two-sided cathode at nonuniform anode polarization] / V. V. Klokov, S. E. Shishkin // Sbornik nauchnyh trudov “Trudy seminara po kraevym zadacham” [Collection of scientific works “Proceedings of workshop on the boundary problems”] [Publishing of Kazan University] – 1985. – V. 22 – P. 117–124. [in Russian]
5. Karimov A. H. Metody rascheta electrohimicheskogo formoobrazovaniya [Methods of calculation of electrochemical shaping] / A. H. Karimov, V. V. Klokov, E. I. Filatov. [Publishing of Kazan University] – 1990. – 387 p. [in Russian]
6. Gazizov E. R. Anodnoe formoobrazovanie dvugrannym katodom pri neravnomernoy plyarizatsii anoda [Anodic shaping by two-sided cathode at nonuniform anode polarization] / E. R. Gazizov, D. V. Maklakov // Izvestiya vuzov. Aviatsionnaya tekhnika [Bulletin of high school. Aviation techniques] – 2002. – No 4. – P. 55–57. . [in Russian]
7. Gazizov E. R. Anodnoe formoobrazovanie krivolineynym katodom pri neravnomernoy plyarizatsii anoda [Anodic shaping by curvplinear cathode at nonuniform anode polarization] / E. R. Gazizov // Izvestiya KGASU [Bulletin KGASU] – Kazan. – 2006. – No 1(5). – P. 132–135. [in Russian]
8. Muksimova R. R. Issledovanie vliyaniya neravnomernosti potentsiala pri electrokhemicheskoy obrabotke v passiviruyuschem elektrolite [Investigation of the influence of potential nonuniformity under electrochemical machining in a passivating electrolyte] / R. R. Muksimova, V. P. Zhitnikov, A. A. Zaripov // Materialy. III nauchno-prakticheskoy konferentsii “Teoriya i practika sovremennykh elertrokhimicheskih proizvodstv” [Collection of works of III scientific conference “The theory and practice of modern electrochemical manufacture“]. Saint Petersburg. – 2014. – P. 37–38. [in Russian]
9. Zaripov A.A. Modelirovanie electrohimicheskoi obrabotki sterzhnevym electrodom-instrumentom v passiviruyuschem electrolite [Modeling of electrochemical machining with a rod electrode tool in passivating electrolyte] / A. A. Zaripov // Sbornik nauchnyh trudov VIII mezhdunarodnoy nauchno-prakticheskoy konferentsii “Teoreticheskie i prikladnye aspekty sovremennoy nauki” [Collection of works of VIII scientific conference “Theoretical and applied problems of modern science“].– Part 1. – Belgorod. – 2015. P. 8–14. [in Russian]
10. Zhitnikov V. P. Primenenie mnogokratnoy fil’tratsii pri chislennom reshenii zadach metodami teorii funktsiy kompleksnogo peremennogo [Application of the multistage filtration at numerical solution of problems by methods of the theory of functions of complex variable] / V. P.  Zhitnikov, N. M. Sherykhalina // Vychislitel’nye tekhnologii [Numerical technologies] – 2013. – V. 18. – No. 1 – P.  15–24. [in Russian]