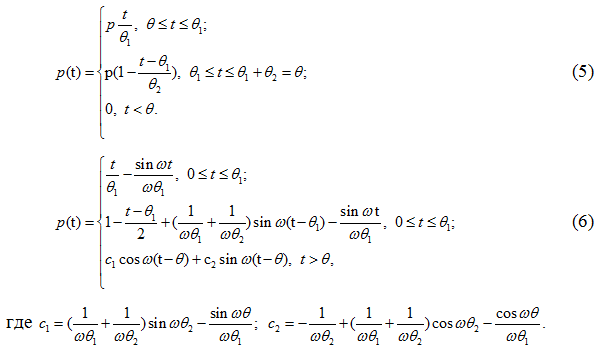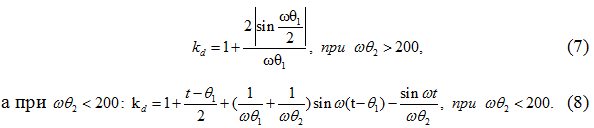РАСЧЕТ БАЛКИ ПОДЗЕМНОГО СООРУЖЕНИЯ ТЕПЛОТРАССЫ ПРИ ИМПУЛЬСНО-СТАТИЧЕСКОЙ НАГРУЗКЕ В УПРУГОЙ СТАДИИ

Сницарь М.А.¹, Самедов А.М.²

¹Аспирант, ²Доктор технических наук, профессор, Национальный технический университет Украины «Киевский политехнический институт»

РАСЧЕТ БАЛКИ ПОДЗЕМНОГО СООРУЖЕНИЯ ТЕПЛОТРАССЫ ПРИ ИМПУЛЬСНО-СТАТИЧЕСКОЙ НАГРУЗКЕ В УПРУГОЙ СТАДИИ

Аннотация

Рассмотрено проблемы расчета балки подземного сооружения теплотрассы при совместном действии импульсных и статических нагрузок в упругой стадии работы. Составлены и решены дифференциальные уравнения движения (перемещения) балки при совместном действии динамических и статических нагрузок. Определены максимальные изгибающие моменты M_max и прогибы Y_max при различных видах закрепления концов балки.

Ключевые слова: импульсно-статические нагрузки, упругая стадия работы, жесткость балки, коэффициент динамичности.

Snitsar M.A.¹, Samedov A.M.²

¹Postgraduate student, ²PhD in Engineering, professor, National Technical University of Ukraine «Kiev Polytechnic Institute»

CALCULATION OF BEAMS UNDERGROUND INSTALLATIONS OF HEATING MAINS UNDER PULSED-LOAD STATIC ELASTIC STAGE

Abstract

The problem of calculating the underground structure of a heating beam under the joint action of pulsed and static loads in the elastic stage of the work. We formulated and solved the differential equation of motion (movement) of the beam under the combined action of dynamic and static loads. Determine the maximum bending moments M_max and deflections Y_max for different types of fixing the ends of the beam.

Keywords: pulse-static load, the elastic stage of operation, the stiffness of the beam, the dynamic factor.

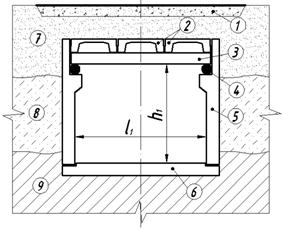
В инженерной практике часто применяются конструкции подземных сооружений в виде шарнирно-опертой балки нагруженной мгновенно-импульсной нагрузкой P(t), и равномерно распределенной статической нагрузкой q от веса вышележащего грунтового слоя, собственного веса самой балки, плиты перекрытия и конструкции автодорожного покрытия.

Рис. 1 - Общий вид подземного сооружения с шарнирно-опертой балкой и автодорога: 1 - асфальтобетонное покрытие дороги; 2 - ребристые плиты перекрытия; 3  - железобетонная балка; 4 - шарнирные катки; 5 - стенки сооружения; 6 - днище сооружения; 7 - грунт из пылеватых песков; 8 - грунт из супеси; 9 - грунт из твердой глины

Рассмотрим данную конструкцию, работающую в упругой стадии на действие кратковременных динамических нагрузок с одной степенью свободы путем задания формы колебаний, совпадающей со статической формой перемещения конструкции под действием рассматриваемой нагрузки.

Движение конструкции шарнирно-опертой балки под действием динамической нагрузкой P(t) может быть описано дифференциальным уравнением:

где A(w) - дифференциальный оператор перемещения, в который входят производные только по пространственным координатам: W (D, t) - перемещение произвольной точки D на поверхности конструкции балки во времени t; p(t) = pf(t) - параметр максимальной мгновенной импульсной нагрузки на 1 пог.м. балки; F₁(D), pf(t) - функция, характеризующая изменение нагрузки по поверхности конструкции балки и функция, соответствующая данному моменту времени; m - вес конструкции.

Динамическое перемещение конструкции шарнирно-опертой балки от импульсной нагрузки можно представить в виде:

где f(D) - функция прогиба балки, описывающая перемещения конструкции балки от действия статической нагрузки q.

Функцию f₁(D) можно определить путем решения дифференциального уравнения следующего вида:

которое удовлетворяет граничным условиям на контуре конструкции балки, зависящим от вида контурных закреплений.

Функцию динамичности передачи импульсной нагрузки и волны сжатия ψ(t) можно описать изменением во времени перемещения конструкции балки, как следствие усилий, возникающих в балке, по методу Бубнова-Галеркина с помощью уравнения для функции ψ(t) в виде колебаний:

где ω - круговая частота собственных колебаний конструкции, соответствующая принятой форме колебаний, совпадающей с формой прогиба от заданной статической нагрузки q при интенсивности f₁(D), в точках перемещения D на поверхности балки.

Значение ω определяется из зависимости функции φ₁(D) f(D) и точки D к массе mf₂(D) и перемещения точки D в следующем виде:

Определив функцию ψ(t) из уравнения (3) находим перемещение конструкции балки на поверхности точки D, в виде W(D, t) в любой момент времени t по (2), а усилия в ней вычисляем по статистическим нагрузкам q на основе уже известных перемещений.

При расчетах значение круговой частоты  можно не вычислять по (4), а принимать равным круговой частоте собственных колебаний конструкции балки, соответствующей той форме колебаний, которая наиболее близка к форме перемещений конструкции со статистической нагрузкой q=q₁+q₂+q_гр от интенсивности f₁(D). Если при расчете конструкции балки, аналитическое выражение для формы перемещения от статической нагрузки q очень громоздко или не находятся в замкнутом виде, динамические усилия и перемещения можно определить умножением соответствующих им статических значений, принимаемых по литературным или справочным данным, на функцию динамичности ψ(t). Эти статические значения можно найти от действия статической нагрузки q, распределенной по поверхности конструкции балки аналогично динамической и равной ее максимальной величине. Наибольшее значение функции динамичности называется коэффициентом динамичности. Он не является постоянной величиной и зависит от вида нагрузки и динамических свойств (массы и жесткости) балки.

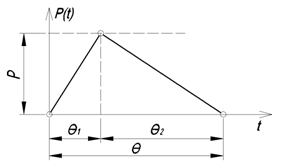
Если динамические нагрузки от транспорта условно принимать мгновенно-импульсного типа, как приведено на рис. 2, в виде изменения во времени, тогда решение данной задачи будет несколько облегчено.

Рис. 2. Закон изменения динамической нагрузки во времени, в виде условно принятого мгновенно-импульсного типа.

При относительно большом времени нарастания нагрузки P(t), когда ω(θ₁) ≥ 20, действие динамической нагрузки P(t) на сооружение можно принимать таким, что практически эквивалентно статической нагрузке интенсивностью p. Например, временную динамическую нагрузку от грузового автотранспорта, условно можно принимать эквивалентной к статической нагрузке, т.е. p(t)=p.

Функции динамичности и коэффициенты динамичности для таких нагрузок можно выразить в следующем виде:

Коэффициент динамичности k_d при ω(θ₂) ≥ 200 следует вычислить как величину достигающую максимальной функции по следующей формуле:

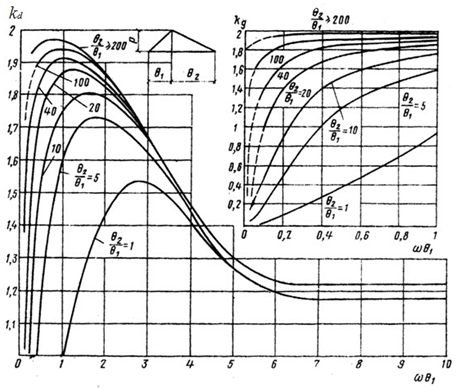
Значение k_d для нагрузок вида показанного на рис. 2 можно определить также по графикам, приведенным на рис. 3.

Рис. 3. Коэффициенты динамичности, при расчете конструкции балки подземных сооружений, в упругой стадии для динамической нагрузки с нарастанием во времени.

Вычисления прогибов и изгибающих моментов в однопролетных балках, загруженных равномерно распределенной статической q и динамической p нагрузками с учетом коэффициента динамичности k_d можно выполнить следующими формулами:

где M_p, Y_p - изгибающий момент и прогиб балки от действия статической q и динамической p нагрузок; M_q, Y_q - изгибающий момент и прогиб от действия статической нагрузки q, определенные методами теории железобетонных конструкций.

Таким образом, зная защемленности балок можно вычислить величины максимальных изгибающих моментов и прогибов балки, как в опорной части, так и в пролете при различных значениях изменения динамической нагрузки во времени θ₁ и θ₂.

При расчетах изменения нагрузки можно принимать постоянными во времени t ≥ θ₂, ωθ₂ ≥ 50 при расчете конструкции в упругой стадии нагружения и ωθ₂ ≥ 300 при расчете в пластической стадии нагружения.

Балка подземных сооружений при действии импульсно-статических нагрузок работает в упругой и упругопластической стадии. Конструкция является наиболее долговечной, когда расчет производятся в упругой стадии работы. Из всех элементов подземных сооружений при динамических нагрузках самым опасным является балка, которая может быть закреплена к конструкциями стенок шарнирными, жесткими, шарнирно-защемленными соединениями. В зависимости от вида закрепления величины изгибающих моментов и прогибов балки имеют разные значения.

Литература

1. Лужин О.В. Динамический расчет сооружений на специальные воздействия / О.В.Лужин, Н.Н Попов, Б.С. Расторгуев. - М.: Стройиздат, 1981. – 215с.
2. Попов Н.Н. Динамический расчет железобетонных конструкций / Н.Н. Попов, Б.С. Расторгуев. – М.: Стройиздат, 1974. – 207 с.
3. Самедов А.М. Расчет и проектирование подземных сооружений мелкого заложения. – Киев, НТУУ "КПИ", 2013. – 851 с.

References

1. Luzhin O.V. Dinamicheskij raschet sooruzhenij na special'nye vozdejstvija / O.V.Luzhin, N.N Popov, B.S. Rastorguev. - M.: Strojizdat, 1981. – 215s.
2. Popov N.N. Dinamicheskij raschet zhelezobetonnyh konstrukcij / N.N. Popov, B.S. Rastorguev. – M.: Strojizdat, 1974. – 207 s.
3. Samedov A.M. Raschet i proektirovanie podzemnyh sooruzhenij melkogo zalozhenija. – Kiev, NTUU "KPI", 2013. – 851 s.