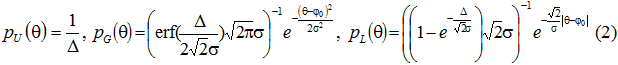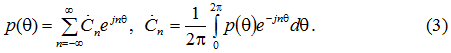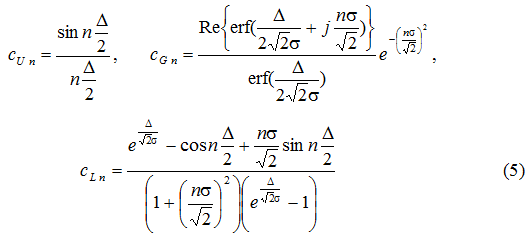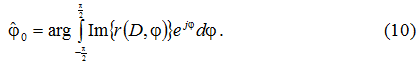ОЦЕНИВАНИЕ НАПРАВЛЕНИЯ ПРИХОДА СИГНАЛА С ИСПОЛЬЗОВАНИЕМ КОРРЕЛЯЦИИ ЗАМИРАНИЙ В MIMO СИСТЕМЕ
Ксендзов А.В.
Кандидат технических наук, Рязанский государственный радиотехнический университет
Работа выполнена в рамках государственного задания № 2014/178
ОЦЕНИВАНИЕ НАПРАВЛЕНИЯ ПРИХОДА СИГНАЛА С ИСПОЛЬЗОВАНИЕМ КОРРЕЛЯЦИИ ЗАМИРАНИЙ В MIMO СИСТЕМЕ
Аннотация
Предложен метод оценивания направления прихода сигнала в условиях рассеивающей среды с помощью многоантенной системы (МАС) из ненаправленных диполей, основанный на Фурье-анализе коэффициентов пространственной корреляции сигналов с последующим вычислением первой комплексной гармоники азимутального спектра мощности (АСМ).
Ключевые слова: MIMO, азимутальный спектр мощности, многолучевость, коррелированные замирания, направление прихода.
Ksendzov A.V.
PhD in Engineering, Ryazan State Radio Engineering University
ESTIMATION OF DIRECTION OF ARRIVAL OF SIGNAL USING FADING CORRELATION IN MIMO SYSTEM
Abstract
A method for estimation of direction of signal arrival in a scattering environment with a multi-element antenna (MEA) consisting of omnidirectional dipoles based on Fourier analysis of spatial correlation coefficients for signals received by MEA with subsequent calculation of the first complex harmonic of the power azimuth spectrum is proposed.
Keywords: MIMO, power azimuth spectrum, multipath, fading correlation, direction of arrival, DoA.
I. Введение
Поскольку в большинстве современных беспроводных систем связи диапазона выше 1 ГГц используемые электромагнитные волны распространяются через среду рассеяния, приводящую к непрерывно меняющейся многолучевой траектории, в математические модели радиоканалов вводятся замирания сигнала и функция азимутального спектра мощности (АСМ) p(θ), что позволяет учесть стохастические свойства среды распространения сигнала. АСМ показывает азимутальное распределение мощности сигнала в точке приема, нормированное следующим образом:
Обычно в моделях используются три вида аппроксимации АСМ: равномерный, гауссовский и лапласовский с возможностью усечения по азимуту [1]. Наличие выделенного направления АСМ отражает свойство принимаемого сигнала концентрировать свою мощность в направлении передатчика даже без луча прямой видимости при распространении в застроенной среде. Таким образом, азимут, соответствующий пику или центру симметрии аппроксимирующей функции, считается направлением прихода (НП). Оценка НП может быть полезна в задачах радиолокации, пеленгации передатчика или кластера отражателей, а также оптимизации многоантенной системы (МАС) для декорреляции замираний сигнала в MIMO системе, что позволяет повысить ее производительность [2]. Данная оценка может быть получена с использованием одиночной вращающейся узконаправленной антенны [3] или фиксированной МАС в сочетании с диаграммообразованием [4].
Цель статьи: разработка метода оценивания НП с помощью МАС из ненаправленных антенн, использующего свойства коррелированных замираний сигнала, проходящего к точке приема через среду интенсивного рассеяния и переотражения.
ll. Главная часть
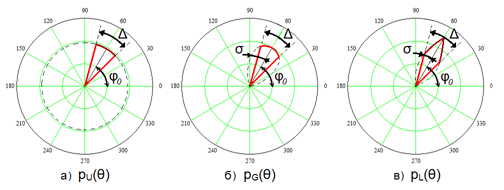
Рассмотрим следующие виды аппроксимации АСМ: равномерную pU(θ), гауссовскую pG(θ) и лапласовскую pL(θ) (рис.1 а, б, в соответственно).
Рис. 1 - Модели аппроксимации АСМ
Полные математические модели данных видов аппроксимации могут быть описаны набором параметров: НП φ0, ширина усечения Δ и угловое расхождение σ для последних двух [1, 2]. Предполагается, что pU(θ) = pG(θ) = pL(θ) = 0 для ![]() и
и
для ![]() , что удовлетворяет нормировке (1).
, что удовлетворяет нормировке (1).
Полагая функцию АСМ p(θ) периодической, представим ее в виде ряда Фурье [5]:
Заметим, что ![]() вследствие (1). Подставляя (2) в (3), получим
вследствие (1). Подставляя (2) в (3), получим
где величины
являются действительными вне зависимости от НП.
Таким образом, из (4) и (5) следует, что при выборе любого из рассматриваемых видов аппроксимации для оценки НП может быть использована фаза первой комплексной гармоники АСМ:
где c – действительный масштабный множитель, a1 и b1 – коэффициенты тригонометрического ряда Фурье, которые могут быть оценены методом, предложенным в [5]. В частности,
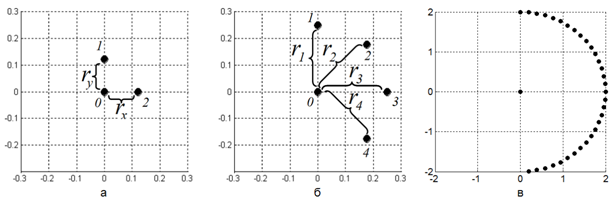
где rx и ry – комплексные коэффициенты корреляции сигналов, принятых парами ненаправленных антенн, как показано на рис. 2 а.
Рис. 2 - МАС для оценивания направления прихода
Каждый из корреляционных коэффициентов может быть оценен как усредненное произведение нормированных комплексных тестовых символов su, sv, полученных соответствующей парой антенн, разнесенных на полярные координаты (D,φ):
Проблемой метода является необходимость чрезвычайно малого антенного разнесения D<0,2 для уменьшения влияния высших гармоник на корреляцию (8) [5]. При этом взаимное влияние антенн и, как следствие, ошибка оценивания, резко возрастает. Для ее уменьшения требуется увеличить размер МАС и количество антенн в ней. К примеру, МАС, изображенная на рис. 2 б, обеспечивает большее разнесение и, следовательно, меньшее взаимное влияние антенн. Коэффициенты тригонометрического ряда Фурье в этом случае:
В предельном случае МАС имеет полукруглую топологию (рис. 2 в) [5], а оценка НП стремится к
III. Выводы
Оценка НП, полученная предложенным методом, содержит случайную и систематическую погрешности. Случайная погрешность вызвана конечной длиной тестовой символьной последовательности и стохастической природой АСМ в целом. Систематическая погрешность может возникнуть из-за асимметрии реального АСМ, что ограничивает область применения метода только сценариями, при которых априори известно о наличии выделенного направления АСМ и возможности его аппроксимации приведенными выше моделями. Также существует компромисс между воздействием взаимного влияния антенн при малом разнесении D и высших гармоник АСМ при большом D на ошибку оценивания. Результаты моделирования показывают, что систематическая погрешность оценки не превышает 1° при использовании МАС, приведенной на рис. 2 б, с D=0,5 и формул (6) и (9) для получения оценки НП при хорошей аппроксимации АСМ (2).
lV. Заключение
Метод, предложенный в данной статье, позволяет оценивать азимут прихода сигнала с использованием многоантенной системы с простой топологией, составленной из ненаправленных элементов без взаимного влияния, которая требуется для сбора информации о пространственной корреляции замираний сигнала, распространяющегося через среду рассеивания. Метод применим к однокластерным канальным моделям с доминирующим направлением, а также может быть применен к многокластерным моделям, например, COST259, для определения средневзвешенного направления на группу отражающих кластеров. Метод неприменим к внутрикомнатным и микросотовым моделям каналов, поскольку соответствующие им АСМ, как правило, носят бесформенный характер.
Литература
- Schumacher L., Pedersen K., Mogensen P. From Antenna Spacings to Theoretical Capacities – Guidelines for Simulating MIMO Systems // Proceedings of 13th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications PIMRC 2002. Lisbon, Portugal, 15-18 Sept. 2002. Vol. 2. P. 587-592.
- Паршин Ю.Н., Ксендзов А.В. Влияние пространственной корреляции на эффективность оптимизации пространственной структуры многоантенной системы при разнесенном приеме // Вестник Рязанского государственного радиотехнического университета. 2006. № 19. С. 54-62.
- Li J., Li X.-Z., Zhou G.-M., Zhang E.-Y. A novel method for estimating the power azimuth spectrum of the wireless channel // IEEE Antennas Wireless Propag. Lett. Dec. 2006. Vol. 5. P. 11–14.
- Wallace J. W., Jensen A. Sparse power angle spectrum estimation // IEEE Trans. Antennas Propag. Aug. 2009. Vol. 57. № 8. P. 2452–2460.
- Ksendzov A. V. A Method for Estimating the Power Azimuth Spectrum Using a Multi-Element Antenna // Proceedings on 16th International Radar Symposium IRS 2015. June 23—26, 2015. V.2. P. 1052–1057.
References
- Schumacher, K. Pedersen, P. Mogensen, “From Antenna Spacings to Theoretical Capacities – Guidelines for Simulating MIMO Systems,” Proc. of 13th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications PIMRC, vol. 2, pp. 587–592, Sept. 2002.
- Parshin and A. Ksendzov, “Effect of spatial correlation on efficacy of MEA optimization when receive diversity,” Vestnik of RSREU, no. 19, pp. 54–62, 2006.
- Li, X.-Z. Li, G.-M. Zhou, and E.-Y. Zhang, “A novel method for estimating the power azimuth spectrum of the wireless channel,” IEEE Antennas Wireless Propag. Lett., vol. 5, pp. 11–14, Dec. 2006.
- W. Wallace and M. A. Jensen, “Sparse power angle spectrum estimation,” IEEE Trans. Antennas Propag., vol. 57, no. 8, pp. 2452–2460, Aug. 2009.
- Ksendzov, “A Method for Estimating the Power Azimuth Spectrum Using a Multi-Element Antenna,” Proceedings on 16th International Radar Symposium IRS 2015, June 23—26, 2015, v.2, pp. 1052–1057. June 2015.