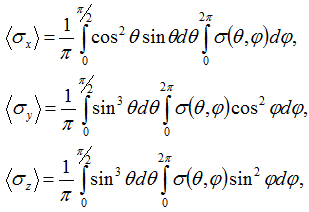ОБОБЩЕННАЯ МОДЕЛЬ ВЯЗКОУПРУГОСТИ ДЕФОРМИРУЕМОЙ ФИЛЬТРАЦИИ, МОДЕЛИРОВАНИЕ МАССОПЕРЕНОСА И ДИФФУЗИИ

Попков В.И.

Кандидат физико-математических наук, доцент Самарского государственного технического университета, старший научный сотрудник СамараНИПИнефть НК «Роснефть»

ОБОБЩЕННАЯ МОДЕЛЬ ВЯЗКОУПРУГОСТИ ДЕФОРМИРУЕМОЙ ФИЛЬТРАЦИИ, МОДЕЛИРОВАНИЕ МАССОПЕРЕНОСА И ДИФФУЗИИ

Аннотация

В статье рассмотрено решение геомеханики явления природной и техногенной сверхпроводимости и уплотнения пластичной деформации кавернозно-порового разупрочнения геосреды. Пластовые деформации в совокупности с динамическими фазовыми моментами  поровой жидкости оказывают влияние на проницаемость и характер фильтрации в уплотненно-разуплотненной области дренирования. Представлено аналитическое решение и анализ нового «второго» закона Дарси (Фика) с учетом энергии вторых моментов деформации.

Ключевые слова: деформация, диффузия, проницаемость, массоперенос, разуплотнение, геосреда

V.I. Popkov

Philosophy Doctor (Physics and Maths), Associate Professor at Samara State Technical University, Senior Research Fellow at “SamaraNIPIneft”, OC “Rosneft”

GENERALIZED VISCOUS-ELASTICITY MODEL OF DEFORMED FILTRATOPN, SIMULATION OF MASS TRANSFER AND DIFFUSION

Abstract

The paper discusses the solution of geo-mechanical phenomenon of natural and man-made super-conductivity and compaction of plastic deformation of geo-sphere cavernous porous strength degradation. Rock deformation in combination with dynamic phase moment in porous fluid provides an effect upon permeability and nature of filtration in compacted/de-compacted drainage area. The author presents the analytical solution and analysis of a new “second” Darcy (Fick’s) Law in view of  deformation second moment energy.

Key words: deformation, diffusion, permeability, mass transfer, de-compaction geo-sphere

Развитие и эволюция трещиноватой сплошной среды - достаточно известная проблема механики, с которой столкнулась наука при описании и моделировании разработки нефтегазовых месторождений [8]. Тема стала особенно актуальна в последние годы, когда к традиционным поровым коллекторам подключены сложнопостроенные  нефте- газонасыщенные, уплотненно-разуплотненные коллектора различной структуры диагенеза [9]. Идентификация таких моделей представляется актуальной задачей современной науки, геологии, разработки, экологии и экономики. Репрезентативность выборки конкретной математической модели и ее параметров влияет на качество проектных решений, гидродинамического моделирования [21].

Пространство состояний, стоячие волны

Введем в рассмотрение пространство состояний, координатами которого являются параметры состояния µⁱ  фазового пространства. Подобной моделью сплошной среды является поровая геосреда [18,19] забоя скважины или субдукции дна океана. Таким сложным состоянием системы служит приток многофазной жидкости, включающий пластичные и твердые субстанции. Для таких моделей считают, что напряжения зависят не только от деформаций и температуры, но от их предыстории.

Определение параметров состояния связано с решением нелинейных задач математически трудной теории распространения волн конечной амплитуды в тяжелой жидкости. Частным видом решений уравнений являются решения типа прогрессивной стоячей волны F(x,y,z,k,ω,t)=Real Ae^i(kr-ωt), где k=k₁i+k₂j+k₃l, , ω - круговая частота,  A - постоянная,  r – радиус-вектор, F - искомые функции. Если k  и ω – постоянные, то волна распространяется как твердое тело, а если - функции состояния, то разные состояния имеют различную скорость и форма деформируется.

Субмикроскопическое равновесие

В субмикроскопической динамике отдельных частиц, описываемой классической механикой, временная симметрия определенно имеет место. Но на практике мы мало что знаем о  поведении отдельных составных частей системы. Важный вопрос состоит в том, достаточно ли исходного знания усредненных «общих» параметров для практического определения динамического поведения системы с адекватной степенью  точности.

На основе анализа результатов исследований по определению размера пор, их распределения и участия в фильтрации, полученных на многочисленных образцах и моделях полевых испытаний с динамическими относительными фазовыми проницаемостями, обоснована новая, более адекватная, модель строения коллекторов и реологии жидкостей с учетом деформации. Она обеспечивает подсчет извлекаемых запасов углеводородов объемным способом с точностью, которая принципиально не может быть достигнута при использовании принятой на сегодня модели на основе закона Дарси и уравнений газовой динамики типа Эйлера [12,14-16].

Выветривание и седиментация порового пространства, поверхности разрывов и трещиноватость

При изучении непрерывных движений жидкости и упругих тел границу между ними можно рассматривать как поверхность разрыва, на которой необходимо выставлять специальные условия, играющие роль краевых условий на подвижных и неизвестных заранее границах. Оказывается, что на поверхностях разрыва между характеристиками движения и состояния должны выполняться некоторые универсальные энергетические соотношения. Для получения непрерывных решений необходимо обращаться к другой, более сложной модели, например, уравнениям движения Навье - Стокса и вводить дополнительные соотношения учета диссипативных эффектов, возникающих за счет резких градиентов распределения скоростей, температур, плотностей, давлений и т.п.

Одним из примеров таких резко неоднородных поверхностей являются структурные поверхности трещиноватости, фациальных и фазовых границ порового пространства. В качестве модели подобной деформируемой структуры выступает модель притока скважины. Задача состоит в том, чтобы построить устойчивое решение развития пласта и скважины во времени и пространстве.

Миграция и диффузия микроструктуры определяются существенно нелинейными процессами взаимодействия физико-химических и гидродинамических  флуктуаций, электромагнитными и тепловыми процессами порождения, конвективного переноса, адсорбции, десорбции и диссипации с последующим осаждением, уплотнением и массопереносом разрушенных частиц по потоку.  В непосредственной близости от поверхности вязкого подслоя можно достоверно описать пульсационные и осредненные характеристики уравнениями Навье-Стокса [1].

Структурная модель

При моделировании пористости со сложной реологией петрофизических свойств широко применяются структурные математические модели, с помощью которых можно описать многие нелинейные эффекты фильтрации, неупругого деформирования и разрушения. Поликристаллический скелет и вязкоупругие свойства моделируются системой слоев, работающих на растяжение - сжатие и вязкое течение. Деформации локального элемента представлены в виде ε_i = e_i + e_i ^p + p_i, где e_i - упругая деформация, e_i^p – пластическая, p_i – ползучести. Ориентация элемента задается углами θ и φ (0≤ θ≤ π/2, 0≤ φ≤2π), рис.1.

Использовались уравнения равновесия [4-7]:

совместности ε(θ,φ)=‹ε_x›cos²θ+‹ε_y›sin²θ·cos²φ+‹ε_z›sin²θ·sin²φ и однородности деформаций  ‹ε_x›=ε(0,φ), ‹ε_y›=ε(π/2,0), ‹ε_z›=ε(π/2,π/2). Здесь σ(θ,φ) - напряжения, ε(θ,φ) - деформации, ‹σ_x›, ‹σ_y›, ‹σ_z›- макронапряжения; ‹ε_x›, ‹ε_y›, ‹ε_z›- макродеформации.

В настоящей работе сделана сравнительная оценка влияния продольных и поперечных колебаний поверхности вязкоупругого слоя на рейнольдсовы напряжения с учетом смешанного нагружения. На основе уравнения массопереноса и сохранения количества движения Навье – Стокса получено энергетически устойчивое обобщение Дарси вплоть до производных вторых моментов, закон квадратичного уплотнения коллекторов [1-10].

 

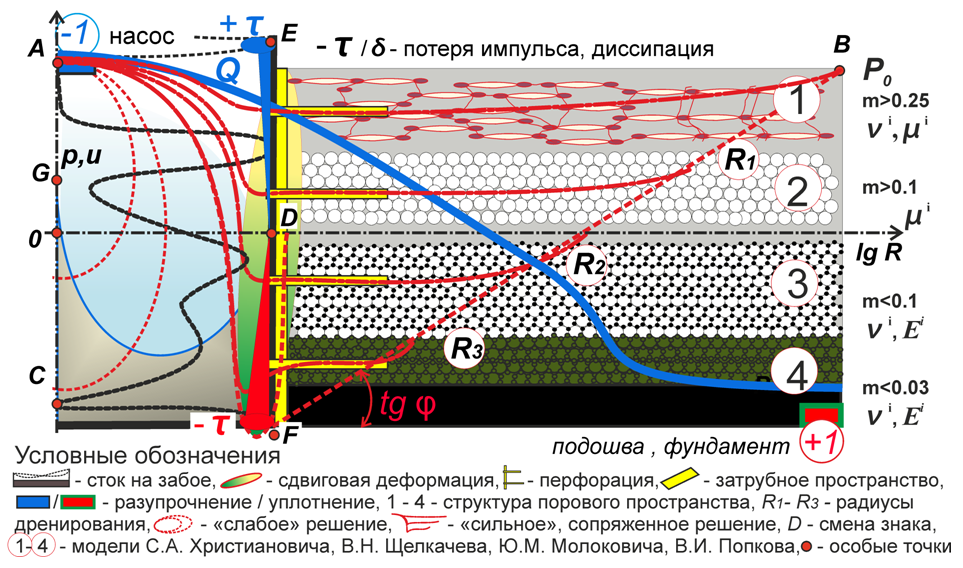
Рис.1 -  Динамический скин-фактор фазового импульса (-/+ τ) системы: насос (А) - коллектор (1 - 3, В) – поровый забой (C)

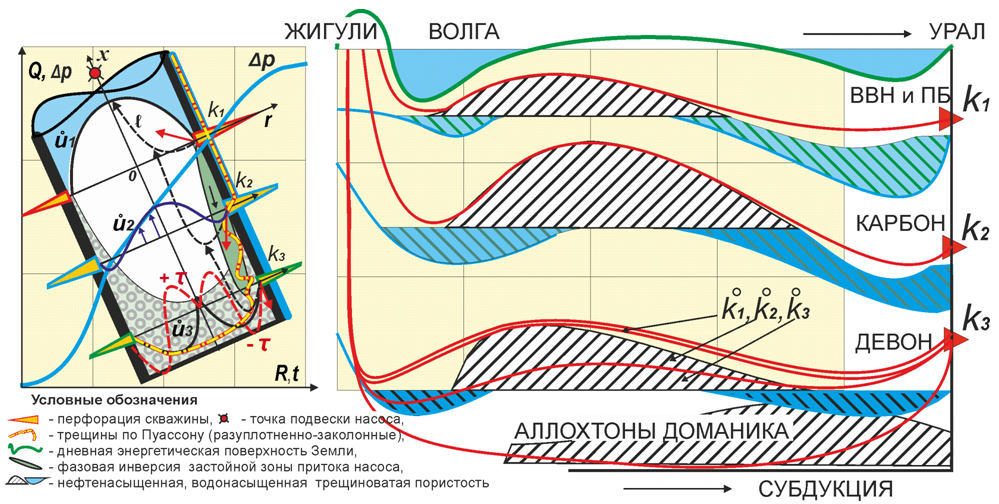
Получено  решение развития поровой структуры, формирования тектонической и кавернообразной трещиноватости. Представлен профиль фильтрации, сопряженный с напряженно-деформированным состоянием поровой структуры геосреды. Проведена верификация геодинамической модели с анализом асимметричных дополнительных граничных условий фазовых границ фронта насыщения, диффузионного замещения, пропитки и насыщения микромасштабов керна [1,13] и макромасштабов субдукции шельфа, рис.2.

Решается линеаризованная система нестационарных уравнений Навье-Стокса, записанные для возмущений скорости относительно осредненой и уравнение неразрывности:

∂v/∂t+1/ρ·∂p/∂x=μ/ρ·∂²v/∂y²,

∂u/∂x + ∂v/∂y+∂w/∂z =0.

Решение ищется в виде бегущей волны: u=h(y)exp i[kx-ωt], v=g(y)exp i[kx-ωt], w=f(y)exp i[kx-ωt], x={x,z}. Задача решается в предположении, что в подслое ∂p/∂y=0,  а пульсационное давление на границе p=p_oexp i[kx-ωt].                               

Граничные условия непротекания и прилипания записываются в виде:

u(x,z,0,t)=-ξ₂∂U/∂y│_y=0+∂ξ₁/∂t·cosθ, v(x,z,0,t)=∂ξ₂/∂t,  w(x,z,0,t)=∂ξ₁/∂t·sinθ.

Рис.2 - Параметризация проводимости скин-слоя деформации забоя скважины и нефте- водонасыщенных поровых ловушек

На вешней границе пульсации u, w заданы и связаны между собой углом скоса  u=A·exp i[kx-ωt], w=B·exp i[kx-ωt], w=u·tgθ, λ_z=λ_xctgθ, B=A·tgθ.

Вертикальная компонента скорости определяется из решения уравнения колебания вязкоупругого слоя под действием пульсационной нагрузки: v=-iωξ₂(h,ω,p_o)exp i[kx-ωt], ξ_i=/ξ_i/exp i[kx-ωt-φ_i], где ξ_i - амплитуды смещения, φ_i - сдвиг фаз относительно пульсационной нагрузки p_o.

Выражение для продольной пульсации скорости получается интегрированием первого уравнения системы. Продольная составляющая представляется в виде вязкостной и волновой составляющих u=u₂+u₁, которые удовлетворяют уравнениям

∂u₂ /∂t = μ/ρ·∂²u₂/∂y²,  ∂u₁ /∂t = - 1/ρ·∂p/∂x.

При условии, что на внешней границе влияние вязкости мало, получаем h(η)=p_o[1-(1+ξ₂/CU'-1/C∂ξ₁/∂t·cosθ)exp(i-1)η]/ρU_o, где U_o=ω/k_x, C=p_o/ρU_o, η=y(ωρ/2μ)^1/2, U'=∂U/∂y│_η=0. Для трансверсальной компоненты f(η)=ctg[1-(1-1/C∂ξ₁/∂t·cos θ)exp(i-1)η].  

Из уравнения неразрывности и граничных условий получаем вертикальную компоненту

g(η)=Ck_x(1+tg θ)/(ωρ/2μ)^1/2[-iη+(1-i)/2(1+iωξ₁/Ccos θ+

+ξ₂U'/C)(exp(i-1)η-1)-iU_o/Cξ₂(ωρ/2μ)^1/2/(1+tg θ)].

Рейнольдсовое напряжение имеет вид:

ρ‹-uv›= -1/4{h(η)g^*(η)+h^*(η)g(η)}=k_xC²(1+tg²θ)/4(ωρ/2μ)^1/2{K₁+K₂ -2Ssinφ₂ –

-[(K₁+K₂)cos η+(K₁-K₂)sin η+(K₁²+K₂²)(cos η-sin η-2S(K₁sin(η+φ₂)+ +K₂cos(η+φ₂))+2η(K₁sin η+K₂cos η)]exp(-η)+(K₁²+K₂²)exp(-2η)},

где S=U_o|ξ₂|(ωρ/2μ)^1/2/C(1+tg²θ), K₁=1+|ξ₂|U'/Ccos φ₂+|ξ₁|ω/Ccos θsin φ₁,

K₂=-|ξ₂|U'/Csin φ₂+|ξ₁|ω/Ccos θcos φ₁.

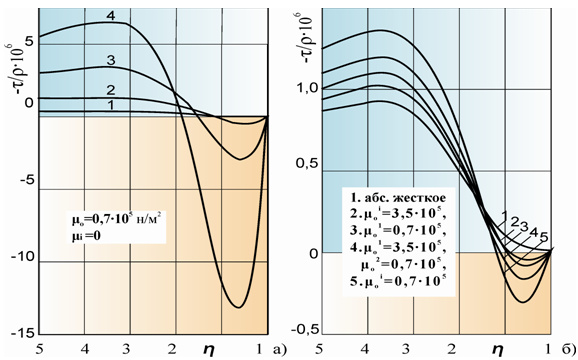
Следовательно, упругая граница индуцирует отрицательное напряжение Рейнольдса, которое экспоненциально затухает и в асимптотике стремится к отношению τ/τ_o=K₁, где τ_o – напряжение гладкой неподатливой поверхности, рис.3. При ω>ω_s, где ω_s – собственная частота упругой поверхности, имеем K₁ > 0, т.е. напряжение превосходит первоначальное в K₁ раз. На упругой поверхности амплитуды напряжений на порядок выше нейтральных. Поверхность продавливается под действием нормального напряжения, гася скорость, но с такой же скоростью и выталкивается по потоку.

Внешний поток U_o определяет фазовую скорость С=0,8U_o и энергетический спектр пульсаций давления [17]:

p(ω)=0,75·10^-5α²ρ²U_o³δ^*[3/2(m-1/m)], ω<ω_o,

p(ω)=1,5·10^-5 (α²ρ²U_o⁶ /ω³δ^*2) [3/2(m-1/m)](2πU_o/5ωδ^*)^m-3,

ω_o=2πU_o/δ=2πU_o/5δ^*, δ=5δ^*,

где δ^* - эффективная толщина пограничного слоя, параметры m=1/С и α (торможения и  Крайчнана), считаются заданными. Величина пульсационного давления задавалась постоянной p(ω)/ρu_*²=1, соответствующей средней величине энергонесущей частоты ω_o.

Рис. 3 - Напряжения Рейнольдса в зависимости от частоты на упругой (а) и вязкоупругой поверхностях на частоте 2000 Гц (б)

При переходе через собственную частоту ω_s при С > a_μ фазовые углы скоростей меняются на 180^o, что приводит к смене знака K₁. Сыпучие и мягкие слои при фазовых скоростях С/a_μ>1 при ω>ω_s способны  индуцировать только отрицательные, снижающие сопротивление трения, напряжения во всем вязком подслое. Амплитуды, возникающие на подобных поверхностях, значительно больше вязкого слоя, а в районе собственной частоты ω_k~1 - в несколько десятков раз.  Упругая поверхность способна уменьшить сопротивление трения при ω_o >ω_s, С > a_μ.

Эффект вязкости поверхности заключается в его апериодичности колебаний, в фазовом сдвиге смещений относительно пульсаций давления. Вязкоупругий слой прогибается под действием пульсаций давления и медленно восстанавливает свою форму, не индуцируя положительных напряжений в поток и тем самым не раскачивает его в отличие от упругого. Вязкоупругая поверхность работает в качестве демпфера, формируя застойные, уплотненные зоны больших временам релаксации, например геологических формаций отложений Доманика или техногенных иловых осадков, рис.2.

Анализируя результаты расчета взаимодействия поверхностей с вязким слоем, можно сделать вывод: максимальным эффектом обладают поверхности, создающие максимальный диффузионный поток при минимальной амплитуде колебаний. В равновесной геологической среде соотношение упругих и вязких свойств оптимальным образом сбалансировано: максимальному уровню диффузионного потока пульсационной энергии соответствует максимальная ее диссипация при минимальных амплитудах колебаний.

При колебании вязкоупругого слоя генерируются отрицательные касательные напряжения, которые при  τ_ω≥ρu_*² могут создавать тягу. Если предположить, что │ξ₂│~ δ_л·10^-1, │ξ₁│~β│ξ₂│, где β ≥1, cos θ ≈1 и φ₂-φ₁=0, то при частотах f ≥1/2π(2/β)^1/2u_*²/ν единица длины колеблющейся поверхности может обеспечить компенсацию вязкого сопротивления трения. Формируется резонансно-сверхпроводящий импульсный выброс мелкодисперсной фракции и микроэлементов «благородных» металлов, обычно содержащихся в нефти, например, ванадия, никеля и т.д. Если рассматривать процесс в геологическом времени и техногенном, то эволюционное усиление деформации проявляются на границах геологических блоков, в т.ч. дренирования и разработки.

Структура порового пространства определяется критическими точками решения A - G, рис.1. Точка А определяет  глубину подвески насоса или выхода канала в атмосферу, D - нулевые напряжения и скорости, т.е. «острова» осаждений вдоль русел. Точка Е - положительному значению рейнольдсового напряжения, т.е. тяговой силе сверхпроводимого канала, с возможным выходом его на поверхность с образованием «озер», которыми изобилует дневная поверхность материков.

Выводы

Процесс динамического взаимодействия потока с поровой структурой теригенных и кавернозно уплотненных карбонатных пластов значительно усложняется при наличии деформируемой поверхности. Числа Рейнольдса при смене масштаба взаимодействия могут возрасти до критических величин отрыва потока. Режим потока при этом изменяется от конфузорного до диффузорного, с образованием теневых шлейфов уплотненной фракции.

Колеблющаяся поверхность генерирует напряжения, пропорциональ-ные квадрату частоты и произведению амплитуд, а также разности фаз

τ_ω= -1/2·ρω²│ξ₂││ξ₁│cos θ·cos(φ₂-φ₁).

С учетом резонансных частот и диссипативных характеристик амплитуды деформации возрастают до критических значений разрушения породы с образованием трещиноватости, которая в геологическом времени аддитивно будет расширяться. При апериодических колебаниях амплитуды прогиба порядка толщины вязкого подслоя, но в геологическом времени эволюционное решение выйдет далеко за его пределы. При этом за фронтом формируется полностью раздробленное поровое пространство той или иной фракции.

Исходя из вязкоупругих свойств коллекторов и модели порового пространства, можно сделать вывод, что деформации происходят с различными скоростями и разными фазовыми углами вязкой диссипации. Этим определяются оптимальные условия применения новых технологий поиска, разведки и разработки высоковязких залежей, многоэтапности и стадийности разработки, ограничения водопритока, «облагораживания» микроэлементами, повышения нефтеотдачи обводненых пластов с учетом энергетического обобщения закона Дарси с учетом моментов деформации.

Решение показывает, что субдукционный комплекс русловых течений образует регулярную решетку на дне океанов и фундаменте из поднятий и опусканий, которые обнаружены НАСА в Атлантическом океане при обработке спутниковых снимков. При этом число островов и озер определяется масштабным фактором геосреды, т.е. кратно 2πn.

Методика позволяет создать и апробировать новый тип многофазных компьютерных программ численных расчетов полей давления и дебитов скважин [20]. Трехфазный гидродинамический симулятор FLORA с динамическими условиями фазового равновесия апробирован как на карбонатных, так и терригенных коллекторах,  маловязких и обводнённых месторождениях, на высоковязких и битумных залежах России и Прикаспия.

Автор благодарен Российскому Научному Фонду «Поддержка и развитие», ФГБОУ ВПО СамГТУ за финансовую поддержку (проект 15-17-00019).

Литература

1. Popkov V.I., Astafiev V.I., Shterenberg A.M., Khamitov I.G., Kolesnikov V.A, Popkova A.V. Global Hydrocarbon Energy Potential of Euro-Asia or Solution of Navier-Stokes Equation for Deformed Micro-Structure of the Earth’s Porous Space. Modern Applied Science. - 9(9). – 2015.- pp. 307-321.
2. Попков В.И., Шакшин В.П., Воропаев Г.А. Блочная самоорганизация дефлюидизации Земли. Кластерная структура простанства времени. Palmarium Academic Publishing. - Saarbrucken. - Germany. - 2012. - 440 c.
3. Попков В.И., Зацепина С.В. Использование зависимости относительных фазовых проницаемостей от капиллярного числа в задачах трехмерного гидродинамического моделирования залежей нефти и газа. Математическое моделирование. 17:2. -2005. - с. 92–102.
4. Астафьев В.И., Кахидзе М.Г., Попков В.И., Попкова А.В. Многомасштабное напряженно-деформированное состояние поровой геосреды, сопряженное с фильтрационным стоком скважины. Вестник СамГУ. 114(4). -2013.- с. 54-75.
5. Радченко В.П., Еремин Ю.А. Реологическое деформирование и разрушение материалов и элементов конструкций. Машиностроение. 1. -М. - -264 с.
6. Радченко В.П, Небогина Е.В. Моделирование неупругого деформирования и разрушения материалов на основании структурной модели. Численные и аналити-ческие методы расчета конструкции. Тр. Междунар. конф. –Самара. -1998.- с. 82–86.
7. Небогина Е.В., Митина Е.В. Численная реализация расчёта ползучести балки при чистом изгибе на основе структурной модели стержневого типа. Математичес-кое моделирование и краевые задачи: Тр. IX Всероссийской науч. конф. с междунар. участием. Ч.1. - Самара. СамГТУ. -2013. - с.144–147.
8. Николаевский В.Н. Собрание трудов. Геомеханика. Разрушение и дилатансия. Нефть и газ. Т.1. НИЦ: Регулярная и хаотическая динамика. Инст. компьютерных исслед. - М. Ижевск. - -640 с.
9. Попков В.И., Гусев В.В., Попкова А.В., Митина Е.В., Каюрин С.А. Геодинамические основы развития проницаемости сложноорганизованных коллекторов. Тр. X Международной научно-практической конф. Ашировские чтения. Т.1. -Туапсе. Самара. -201 -с. 213-236.
10. Миронова Е.А., Попков В.И., Зацепина С.В. Собственные формы самоорга-низации порового пространства и напряженно-деформируемого состояния земной коры. Тр. X Международной научно-практической конф. Ашировские чтения. Т.2 - Туапсе. Самара. – 2014. - с.103-111.
11. Попков В.И., Мамаева Е.И., Попков К.В. Основные направления освоения углеводородного потенциала континентального шельфа РФ. Тр. X Международной научно-практической конф. Ашировские чтения. Т.2. - Туапсе. Самара. – 2014. - с.166-174.
12. Баутин С.П., Обухов А.Г. Одно точное стационарное решение системы уравнений газовой динамики. Известия ВУЗов. Нефть и Газ. №4. – 2013.- с. 81-86.
13. Рощин П.В, Васкес Карденас Л.К., Тананыхин Д.С., Стручков И.А. Лабораторное исследование процесса вытеснения тяжелой высоковязкой нефти в карбонатном керне при помощи ренгеновского компьютерного томографа. Тр. X Международной конф. Ашировские чт. Т.2. -Туапсе. Самара.- 2014. - с. 220-224.
14. Баландин Л.Н., Астафьев В.И., Гребенников О.А. Математическая модель процесса вывода на режим скважины, оборудованной УЭЦН. SPE-171306-RU. -2014. - c. 1-9.
15. Кожевников Е.Н., Самойлова Я.В. Пространственно модулированные струк-туры в нематическом жидком кристалле при воздействии осцилирующего течения Куэтта на сверхнизких частотах. Вестник СамГУ. Естественнонаучная сер. - №6(97). - с. 113-123.
16. Самельсон Р.Н., Виггинс С. Лагранжев перенос в геофизических струях и волнах: подход на основе теории динамических систем. НИЦ: Регулярная и хаотическая динамика. Инст. компьютерных иссл. - М. Ижевск. - -192 с.
17. Акустика океанской среды / Под ред. Л.М. Бреховских, И.Б. Андреевой. - М. Наука. - 1989. - 222 с.
18. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Статистическая физика. Т.V(1).- М. Физматлит. - 2002. - 616 с.
19. Пенроуз Р. Путь к реальности, или законы, управляющие Вселенной. Пол-ный путеводитель. Инст. компьютерных исслед. НИЦ: Регулярная и хаотическая динамика. -М. Ижевск. -2007. -912 с.
20. Манырин В.Н., Фахретдинов Р.Н., Попков В.И. ТРИАС. Блок гидродинами-ческого моделирования. Гидродинамический симулятор. Свидетельство ППП ЭВМ №2005612893 от 09.11.05г.
21. Попков В.И., Миронова Е.А., Зацепина С.В. Разработка и геодинамическое моделирование порово-диффузионной разгрузки многомасштабных сложнооргани-зованных коллекторов. Международный независимый институт Математики и Систем "МиС". -№ 5(16). -2015. -с. 39-48.

Reference

1. Popkov V.I., Astafiev V.I., Shterenberg A.M., Khamitov I.G., Kolesnikov V.A, Popkova A.V. Global Hydrocarbon Energy Potential of Euro-Asia or Solution of Navier-Stokes Equation for Deformed Micro-Structure of the Earth’s Porous Space. Modern Applied Science. - 9(9). – 2015.- pp. 307-321.
2. Popkov V.I., Shakshin V.P., Voropaev G.А. Block-type Self-organization fot he Earth’s Defluidization Cluster structure of time space. Palmarium Academic Publishing. - Saarbrucken. - Germany. - 2012. – pp. 440.
3. Popkov V.I., Zatsepina S.V. Use of Relative Phase Permeability Dependence vs. Capillary Number in Resolving the Tasks of 3D Hydro-dynamic Oil and Gas Reservoir Simulation. Mathematical Modeling. 17:2. -2005. - pp. 92–102.
4. Astafiev V.I., Kakhidze M.G., Popkov V.I., Popkova A.V. Multi-scaled Stress Deformed Status of Porous Geosphere Conjugated with Well Filtration Outflow. Bulletin of SamSU. 114(4). -2013.- pp. 54-75.
5. Radchenko V.P., Eremin Yu.A. Rheological Deformation and Destruction of Meterials and Structural Elements. Machine-building. 1. -М. -2004. -264 p.
6. Radchenko V.P., Nebogina Е.V. Modeling of Non-elastic Deformation and Destruction of Materials at the Basis of Structural Model. Numerical and Analytical Methods to Calculate the Structures. Papers to International Conference. – Samara -1998.- pp. 82–86.
7. Nebogina Е.V., Mitina Е.V. Numerical Realization of Beam Creeping Calculation with Obvious Bending at the Basis of Bar-type Structural Model. Mathematical Modeling and Marginal Tasks: Papers to IX All-Russian Scientific Conference with Foreign Participation. Part 1. - Samara. SamSTU. -2013. - pp.144–147.
8. Nikolayevskiy V.N. Collected Papers. Geomechnics. Destruction and  Oil and Gas. Volume 1. R&D Center: Regular and Chaotic Dynamics. Institute of Computer Studies. - М. Izhevsk. - 2010.  -640 p.
9. Popkov V .I., Gusevв V.V., Popkova A.V., Mitina Е.V., Kayurin S.А. Geo-dunamic Basis of Permeability Development in Complexly-organized Resevoirs. Papers to X International Scientific and Application Conference. Readings from Ashirov. Volume –Tuapse. Samara. -2014. – pp. 213-236.
10. Mironova Е.А., Popkov V.I., Zatsepina С.В. Independent Forms of Self-Organization with Porous Media and Stress-Deformed Status oft he Earth’s Crest. Papers to X International Scientific and Application Conference. Readings from Ashirov. Volume 2 - Tuapse. Samara. – 2014. - 103-111.
11. Popkov I., Mamaev Е.I., Popkov К.V. Basic Trends in Developing Hydrocarbon Potential at the Russian Off-shore. Papers to X International Scientific and Application Conference. Readings from Ashirov. Volume 2 - Tuapse. Samara. – 2014. - pp.166-174.
12. Bautin S.P., Obukhov А.G. One Exact Stationary Solution of a System of Equations for Gas Dynamics. Bulletic of HEI. OIl and Gas. No. 4. – 2013.- 81-86.
13. Roschin P.V., Vasquez Cardenas L.K., Tananykhin D.S., Struchkov I.А. Lab Studies Heavy Oil Displacement Process from Carbonate Cores and Application of X-Ray Computer Tomograph. Papers to X International Scientific and Application Conference. Readings from Ashirov. Volume 2 - Tuapse. Samara. - - pp. 220-224.
14. Balandin L.N., Astafiev V.I., Grebennikov О.А. Mathematical Model of Well Commissioning Process Having ESP. SPE-171306-RU. -2014. - pp.1-9.
15. Kozhevnikov Е.N., Samoilova Ya.V. Spatial Structure Modeling in Nematic Liquid Crystal Under Effect of Couette Oscillation Flow in Conditions of Super-Low Frequencies. Bulletin of SamSU. Ser. of Natural Sciences. -2012. №6 (97). - pp. 113-123.
16. Samelson R.N., Wiggins S. Lagrange’s Transfer In Geo-physical Jets and Waves: Approach at the Basis of Dynamic System Theory. R&D Center: Regular and Chaotic Dynamics. Institute of Computer Studies. - М. - 2009. -192 p.
17. Acoustics in Oceanic Media / edited by L.V. Brekhovskikh, I.B. Andreeva. - М. Nauka. - 1989. - 222 p.
18. Landau D., Lifshitz Е.М. Theoretical Physics. Statistical Physics. V (1).- М. PhysMatLit. - 2002. - 616 p.
19. Penrose R. Way to Reality or Law That Govern the Universe. Guide-book. Institute of Computer Studies. R&D Center: Regular and Chaotic Dynamics. -М. Izhevsk. -2007. - 912 p.
20. Manyrin V.N., Fakhretdinov R.N., Popkov V.I. TRIAS. Block of Hydro-dynamic Modeling. Hydro-dynamic Simulator. Certificate PPP ЭВМ №2005612893 dt. 09.2005.
21. Popkov V.I., Mironova Е.А., Zatsepina S.V. Development and Hydro-dynamic Modeling of Porous-Diffusive Uploading in Large-scaled Complexly Organized Reservoirs. International Independent Institute on Maths and “MiS” Systems –No. 5(16). -2015. pp. 39-48.