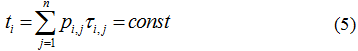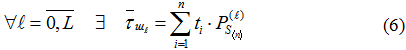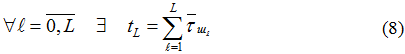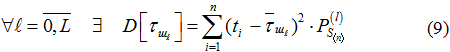НАХОЖДЕНИЕ ХАРАКТЕРИСТИК КОНЕЧНЫХ МАРКОВСКИХ ЦЕПЕЙ ПРИ ПРОИЗВОЛЬНЫХ ШАГАХ ПЕРЕХОДОВ

Цимбал В.А.¹, Шиманов С.Н.², Тоискин В.Е.³

¹Доктор технических наук, ²Доктор технических наук, ³Кандидат технических наук, МОУ «Институт инженерной физики»

НАХОЖДЕНИЕ ХАРАКТЕРИСТИК КОНЕЧНЫХ МАРКОВСКИХ ЦЕПЕЙ ПРИ ПРОИЗВОЛЬНЫХ ШАГАХ ПЕРЕХОДОВ

Аннотация

В статье представлен методический подход к анализу характеристик неоднородных конечных марковских цепей при разных шагах переходов. Предложен подход к определению вероятностно-временных характеристик и временных характеристик.

Ключевые слова: сеть передачи данных (СПД), конечная марковская цепь (КМЦ), шаг перехода из состояния в состояния КМЦ, фиктивные состояния, неоднородная КМЦ.

Tsimbal V.A.¹, Shimanov S.N.², Toiskin V.E.³

¹Doctor of Technical Sciences, ²Doctor of Technical Sciences, ³Candidate of Technical Sciences, MOU «Institute of engineering physics»

FINDING OF CHARACTERISTICS OF FINITE MARKOV CIRCUITS AT THE ARBITRARY STEPS OF PASSAGES

Abstract

In article final chain Marcova with different steps of transitions in which there is a reduction of length of all steps to the minimum is presented. The concept of the fictitious conditions providing adequacy of generated final chain Marcova to physical process is thus entered. The approach by definition of is likelihood-time characteristics and time characteristics of non-uniform final chains Marcova with identical and different step of transition from a condition in conditions of final chain Marcova is offered.

Keywords: data transmission network (DTN), final chain Marcova (FCM), a step of transition from a condition in conditions FCM, fictitious conditions, non-uniform FCM.

Конечные марковские цепи (КМЦ) широко используются при описании циклических процессов, проистекающих во многих технических системах, в частности, в системах радиотехнического и телекоммуникационного профиля [1,2]. Например, процесс функционирования сети передачи данных (СПД) хорошо описывается КМЦ. Это обусловлено тем, что [3,4]: - процесс доставки сообщений в СПД является случайным, что вытекает из наличия в каналах связи (КС) помех, приводящих к искажениям передаваемых бит информации; - физика процесса доставки сообщений в СПД подтверждает соблюдение в нем марковского свойства; - изменение состояния данного процесса происходит в дискретные моменты времени, вызванные передачей информационного или квитанционного кадров; - количество состояний рассматриваемого процесса счетно и конечно. Именно эти свойства и лежат в основе определения такого случайного процесса как конечная марковская цепь. Различают поглощающие и эргодические КМЦ. В первом случае в КМЦ имеется одно или несколько поглощающих состояний, во втором - таковые отсутствуют. Случайный процесс, попав в поглощающее состояние, выйти из него уже не может. Здесь рассматриваются только поглощающие КМЦ.

Основными характеристиками КМЦ, находимыми в различных исследованиях, как правило, являются вероятностно- временные (ВВХ) и временные характеристики (ВХ), при этом исходными данными для анализа являются матрица переходных вероятностей (МПВ) и вектор вероятностей начальных состояний КМЦ.

В случае, когда КМЦ является однородной (МПВ неизменна от шага к шагу) и шаг переходов (ШП) по всей цепи одинаков, нахождение ВВХ и ВХ осуществляется известными подходами теории КМЦ [2-4].

Отметим, что под ВВХ понимается динамика вероятностей состояний КМЦ на i-м шаге, и они описываются уравнением Колмогорова-Чепмена (УКЧ):

где  - вектор вероятностей состояний КМЦ на нулевом шаге (вектор начальных состояний);

 - вектор вероятностей состояний КМЦ на i-м шаге;

P_[n,n] - МПВ КМЦ.

Под ВХ понимается математическое ожидание (МО) числа шагов M[L], затрачиваемое процессом для перехода из l-го состояния в поглощающее и дисперсия D[L] (среднее квадратическое отклонение σ[L]  (СКО)) числа таких шагов. Определения ВХ поглощающей КМЦ осуществляется по фундаментальной матрице (ФМ) N_[n-r,n-r], получаемой из матрицы Q_[n-r,n-r], сформированной из МПВ P_[n,n], где r – количество поглощающих состояний КМЦ. ФМ имеет вид:

где I – единичная матрица размером (n-r)×(n-r).

МО числа шагов M[L], затрачиваемое процессом для перехода из l-го состояния в поглощающее, равно сумме элементов последней строки ФМ.

Дисперсия числа шагов D[L] находят по так называемой дисперсионной матрице (ДМ), получаемой по формуле:

где N_dg[n-r,n-r] - диагональная матрица, полученная из ФМ заменой всех элементов нулями, кроме элементов главной диагонали; N_sg[n-r,n-r] - матрица, полученная из диагональной возведением каждого ее члена в квадрат.

Дисперсия числа шагов D[L], затрачиваемых процессом для перехода из l-го состояния в поглощающие, равно сумме элементов последней строки ДМ (3).

Переход к реальному времени при нахождении ВВХ на l-м шаге процесса в классической теории КМЦ осуществляется умножением текущего числа шагов на длину шага τ_ш, т.е. t_l=l·τ_ш. Переход к реальному времени при нахождении МО и дисперсии осуществляется так:

Однако, во многих практических случаях в КМЦ ШП разные. Это актуально, например, для СПД, у которых процесс доведения сообщений сопровождается как передачей на канальном уровне повтора информационного кадра (ИК), так и квитанционного кадра (КК) о верном или неверном доведении ИК. Учитывая, что длины ИК и КК разные, а скорость передачи информации как в прямом, так и в обратном каналах чаще всего одинакова, возникает проблема определения ВХ и ВВХ по описывающей данный процесс КМЦ с разными ШП. Снять данное ограничение классической теории КМЦ позволяют метод «фиктивных состояний» и метод «среднего шага переходов».

Метод фиктивных состояний заключается в следующем [5,6]. Среди всех ШП анализируемой КМЦ, кроме перехода «сам в себя», выделяется наименьший и все остальные шаги нормируются по нему. Причем, наименьший ШП рассматриваемой КМЦ является наибольшим общим делителем всех её ШП. Во все переходы с «длинными» шагами вводится дополнительно фиктивные состояния, причем их число равно норме «длинного» шага по отношению к «короткому» без единицы. Переход в первое фиктивное состояние некоторого перехода осуществляется с имеющейся ПВ, а переходы из одного фиктивного состояния в другое, а также из последнего фиктивного состояния в искомое происходит с вероятностью 1. Таким образом, во всей КМЦ ШП выравнивается по самому короткому шагу. Последнее позволяет использовать классический подход к нахождению ВХ и ВВХ КМЦ.

Недостатком этого метода является существенное увеличение числа состояний КМЦ при большом временном разбросе значений ШП и как следствие - увеличение размеров МПВ. При этом МПВ будет увеличиваться только за счет введения нулевых элементов, что не приводит к её усложнению, а следовательно, и не усложнит трудоемкий процесс нахождения самих переходных вероятностей (ПВ). Однако метод фиктивных состояний при большом числе разных ШП анализируемой КМЦ требует нахождения наибольшего общего делителя и модификации КМЦ, которая становится разреженной, что вызывает сложности при её обращении.

Для этого случая используется метод среднего шага переходов [4]. Его суть заключается в следующем. Пусть имеется КМЦ с n состояниями, переходы между которыми происходят с разными шагами. Аналогично МПВ P_[n,n] для КМЦ вводится матрица шагов переходов (МШП) T_[n,n], при этом каждой ПВ p_i,j соответствует свой шаг . КМЦ рассматривается в переходном режиме за L шагов. Распределение вероятностей КМЦ на нулевом шаге задано вектором , финальное распределение вероятностей – вектором . Для каждого i-го состояния КМЦ вводится частный средний ШП во все состояния:

и для всей КМЦ средний ШП на текущем ℓ-­м шаге .

В основу метода среднего шага переходов положены следующие доказанные утверждения.

Утверждение 1. Средний ШП в КМЦ с разными ШП на каждом текущем шаге ℓ является своим, т.е. если τ_i,j≠const, то:

Утверждение 2. Средний шаг в КМЦ с разными ШП зависит от начального распределения вероятностей состояний, т.е. если τ_i,j≠const, то:

Утверждение 3. Реальное среднее время за L шагов КМЦ с разными ШП τ_i,j равно:

Утверждение 5. Дисперсия «среднего шага» в КМЦ с разными ШП на каждом текущем шаге ℓ является своей, т.е. если τ_i,j≠const, то:

Утверждение 6. Средний ШП эргодической КМЦ с разными ШП с течением времени стремится к постоянной величине, т.е. если τ_i,j≠const, то:

Утверждение 7. Средний ШП поглощающей КМЦ с разными ШП с течением времени стремится к ШП поглощающего состояния, т.е. если τ_i,j≠const, то:

Утверждение 8. Дисперсия «среднего шага» в эргодической и поглощающей КМЦ с разными ШП с течением времени стремится нулю, т.е. если τ_i,j≠const, то:

Утверждение 9. Среднее время перехода КМЦ из состояния i в состояние j при разных ШП равно:

где M[S_k] - среднее число шагов, проводимых процессом в k-м сообщающемся состоянии (находится по ФМ (2)); τ_k - частный средний ШП для k-го состояния.

Утверждение 10. Дисперсия времени перехода КМЦ из состояния i в состояние j при разных ШП равна:

где D[S_k] - дисперсия числа шагов, проводимых процессом в k-м состоянии (находится по ДМ (3)).

Таким образом, для нахождения ВВХ по методу среднего шага переходов необходимо использовать УКЧ (для нахождения вектора вероятностей состояний) и воспользоваться один раз выражением (5) и на каждом шаге решения УКЧ выражениями (6), (8) и (9) для нахождения длины конкретного шага и длительности всего процесса в целом. Для нахождения ВХ достаточно воспользоваться выражениями (13) и (14) в совокупности с выражением (5).

В телекоммуникационных системах процесс доведения сообщений зачастую имеет нестационарный характер, что объясняется, например, изменением вероятности ошибки на элементарный символ в сеансе связи и др.

Соответствующая таким реальным процессам КМЦ является неоднородной, т.к. компоненты (ПВ) МПВ у неё меняется от шага к шагу. Кроме того, в такой КМЦ ШП могут быть также как одинаковыми, так и разными.

Нахождение ВВХ в неоднородной КМЦ при одинаковых ШП осуществляется по известному УКЧ в следующей модификации [7]:

где  - МПВ на i-м шаге КМЦ.

Длительность анализируемого процесса будет зависеть от числа шагов так: t_i=i·τ_ш.

Нахождение ВХ (M[L] и M[L]) базируется на получении из МПВ ФМ и ДМ. Но МПВ на каждом шаге КМЦ своя. Следовательно, на каждом шаге l могут быть получены свои M[L]_l и D[L]_l. К их усреднению могут быть применены разные подходы. Один из них заключается в следующем. Для всех L шагов находятся МПВ, а затем на их множестве для каждого шага строится матрица дисперсий ПВ. Суммированием всех дисперсий такой матрицы получаем для неё некий коэффициент. Нормируя данные коэффициенты по всему множеству МПВ, получаем весовые коэффициенты для каждой МПВ. Именно они и будут использованы для усреднения M[L] и D[L] на всем множестве шагов.

Нахождение ВВХ в неоднородной КМЦ при разных ШП осуществляется также по УКЧ (15), при этом на каждом шаге УКЧ дает вектор вероятностей состояний. Для нахождения длительности процесса при разных ШП также используется метод среднего шага переходов. При этом на каждом текущем шаге необходимо воспользоваться выражениями (5), (6), (8) и (9) для нахождения длины конкретного шага и длительности всего процесса в целом.

Нахождение ВХ в неоднородной КМЦ при разных ШП осуществляется комбинацией подходов для случая однородной КМЦ и разных ШП и случая неоднородной КМЦ и одинаковых ШП. Это допустимо в силу независимости процедур нахождения среднего текущего шага и процедуры нахождения весовых коэффициентов для усреднения M[L] и D[L] на всем множестве шагов.

Литература

1. Олифер В.Г., Олифер Н.А. Основы сетей передачи данных. Курс лекций. Учебное пособие/Издание второе исправное/ - М.: Интуит.ру «Интернет-университет Информационных Технологий», 2005 – 176с.
2. Казаков В.А. Введение в теорию марковских процессов и некоторые радиотехнические задачи.-М.: Сов.радио, 1973.
3. Кемени Джон Дж., Снелл Дж. Ларк. Конечные цепи Маркова./Пер. с англ. – М.: Наука, 1970.
4. Цимбал, В. А. Информационный обмен в сетях передачи данных. Марковский подход : монография [Текст] / В. А. Цимбал. – М.: Вузовская книга, 2014. – 144 с.: ил.
5. Цимбал В.А., Косарева Л.Н. Метод фиктивных состояний определения характеристик конечных марковских цепей при разной длине шага переходов. /VI международная конференция. – г. Пущино. – 1999. – С.286.
6. Цимбал В.А. Нахождение характеристик реальных процессов на основе метода фиктивных состояний. - М.: Измерительная техника №12, 2001.
7. В.А.Цимбал, М.Ю.Попов, М.Ю.Дробышев Математическое моделирование процесса доведения сообщения в радиосети без обратной связи с повторениями и накоплением информации / Информационные технологии в проектировании и производстве №3,2010/ – Москва. - С.78 - 83

References

1. Olifer V.G., Olifer N.A. Osnovi setej peredachi dannih. Kurs lekcij. Uchebnoe posobie. / Izdanie vtoroe ispravlennoe / - М.: Intuit.ru «Internet-universitet informacionnih tehnologij», 2005 – 176s.
2. Kazakov V.А. Vvedenie v teoriu marcovskih processov I nekotorie radiotehnicheskie zadachi.-М.: Sov.radio, 1973.
3. Kemeni Djon Dj., Snell Dj. Lark. Konechnie cepi Markova / Per. s angl. – М.: Nauka, 1970.
4. Tsimbal, V. А. Informacionnij obmen v cetyah peredachi dannih.Markovskij podhod: monografiya. / V. А. Tsimbal. – М.: Vuzovskaya kniga, 2014. – 144 s.: il.
5. Tsimbal, V. А. Metod fiktivnih sostoyanij opredeleniya harakteristik konechnih markovskih cepej pri raznoj dline shaga perehodov // V. A. Tsimbal, L. N. Kosareva / VI mejdunarodnaya konferenciya. – g. Push’ino. – 1999. – S.286.
6. Tsimbal, V. А. Nahojdenie harakteristik realnih processov na osnove metoda fiktivnih sostoyanij. - М.: Izmeritelnaya tehnika №12, 2001.
7. Tsimbal, V. А. В.А.Цимбал, М.Ю.Попов, М.Ю.Дробышев Matematicheskoe modelirovanie processa dovedeniya soobsheniya v radioseti bez obratnoj svyazi s povtoreniyami I nakopleniem informacii / Informacionnie tehnologii v proectirovanii i proizvodstve №3,2010/ – M.: - S.78 - 83