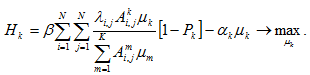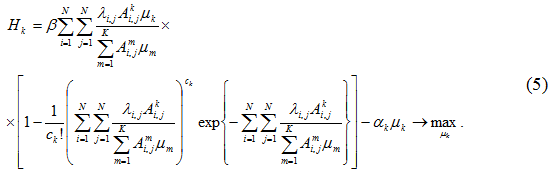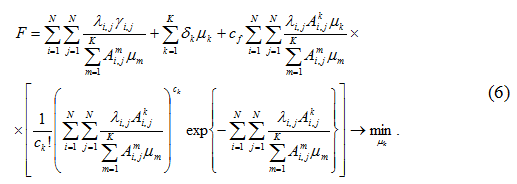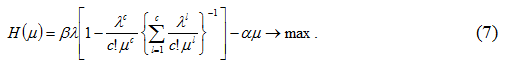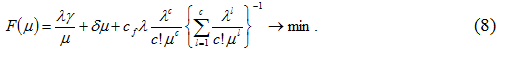МОДЕЛИРОВАНИЕ ТРАНСПОРТНОГО СРЕДСТВА КАК МНОГОКАНАЛЬНОЙ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ С ОТКАЗАМИ

Баламирзоев А.Г.¹,  Баламирзоева Э.Р.², Гаджиева А.М.³

 ¹Доктор технических наук, ^2,3Аспирант, Махачкалинский филиал МАДИ

МОДЕЛИРОВАНИЕ ТРАНСПОРТНОГО СРЕДСТВА КАК МНОГОКАНАЛЬНОЙ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ С ОТКАЗАМИ

Аннотация

В статье рассмотрено моделирование транспортного средства как многоканальной системы массового обслуживания с отказами. Приведен численный пример решения поставленной задачи и показан прибыль двумя способами.

Ключевые слова: моделирование, транспортное средство, пассажиропоток, маршрут.

Balamirzoev A.G.¹,  Balamirzoeva E.R.², Gadzhieva A.M.³

¹Doctor of Technical Sciences, ^2,3Graduate, Makhachkala branch MADI

MODELING THE VEHICLE AS A MULTI-CHANNEL QUEUEING SYSTEMS WITH BREAKDOWNS

Abstract

The article describes the modeling of the vehicle as a multi-channel queueing systems with breakdowns. The numerical example of solving the task shown a profit in two ways.

Keywords: modeling, vehicle, passenger, route.

Моделирование взаимодействия участников транспортной системы требует нового подхода для развития системы городских пассажирских перевозок в России. Появляются конфликтные ситуации, так как существуют множество участников, имеющих несовпадающие интересы.

Требует применения новых методов исследования поведения поставщиков и потребителей товаров и услуг при  переходе экономики к рыночным механизмам функционирова­ния.

Функционирование городского пассажирского транспорта (ГПТ) происходит в условиях ограничений. Изменения, которые про­изошли в России в 1990-е годы, связаны еще и с тем, из-за неудовлетворительной экономики  государ­ство не могло финансировать многие отрасли, в  том числе  ГПТ. Городской транспорт в Рос­сии и в большинстве других стран является убыточным, и не всегда бюджетных средств достаточно для покрытия убытков транспорт­ных предприятий. Поэтому возникает задача оптимизации работы ГПТ в условиях ограничений на бюджетное финансирование. Заведомо задача сводится к  обеспечение надлежащего качества транспортного обслуживания пассажиров при заданном объеме финансирования.

Крайне важно ограничение на пассажировместимость под­вижного состава, так как на каждом маршруте рекомендуется экс­плуатировать транспортные средства одинаковой вместимости, а решение оптимизационных задач может привести к нарушению нормативов по загрузке транспортного средства, что снизит каче­ство обслуживания пассажиров.

Особую сложность представляет собой тот факт, что пассажиропоток и поток транспорта являются случайными процессами и избежать переполнения под­вижного состава нельзя. В [3] представлена работа общест­венного транспорта на одном маршруте как объемная система мас­сового обслуживания.

Наблюдается увеличение, в последнее время, количества мар­шрутов и интенсивности движения транспорта, в том числе и об­щественного.

С одной стороны, это способствует более качествен­ному обслуживанию пассажиров (уменьшается время ожидания на остановочном пункте, появляется возможность выбора вариан­та передвижения и т.д.). С другой стороны, приводит к ухудшению экологической обста­новки, рост интенсивности работы транспорта, повышает опасность перегрузки дорог, а увеличение коли­чества маршрутов — к излишней конкуренции между перевозчи­ками за пассажиров, что снижает безопасность движения.

Так как потоки транспорта и пассажиров случайные, появляется сложность процесса перевозки пассажиров. Если дви­жение транспорта по одному маршруту можно стабилизировать (сделать поток транспорта близким к детерминированному) с по­мощью диспетчерского управления, то для множества маршрутов это сделать практически невозможно. Управлять массой людей значительно сложнее, чем несколькими автобусами, так как в любом случае поток пассажиров является случайным.

Системой массового обслуживания является каждая единица подвижного состава общественного транспорта. Оно пред­ставляет собой многоканальную систему массового обслуживания без блока ожидания, если при этом рас­сматривать каждое транспортное средство отдельно.

Будем считать, для упрощения модели, что пассажиры, полу­чившие отказ в обслуживании (нет свободного места в транспорт­ном средстве), покидают остановочный пункт. Этот факт является отрицательным как для пассажира и транспортного оператора (не получившего дополнительный доход от оплаты проезда), так и для системы «город» (потому что пассажир может выбрать другой, бо­лее затратный способ перемещения).

Введем следующие параметры: c_k — максимальное количест­во пассажиров, которое может перевезти маршрут k. Этот параметр соответствует количеству мест в обслуживающей системе (в данном случае в единице подвижного состава, движущегося по маршруту).

Пассажиропоток распределяется пропорционально интен­сивности движения транспорта на данном маршруте [1-3] то­гда средняя доля маршрута l оператора k от пассажиропотока между пунктами i и j

Общее количество пассажиров, перевезенных на маршруте k, исходя из (1) составит:

Интенсивность спроса на пере­движение на маршруте k описывает данный показатель. Учитывая, что интенсивность обслужи­вания µ_k, получим коэффициент

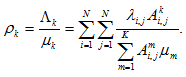
Основным предположением является то, что потоки транспор­та и пассажиров — пуассоновские. Следовательно, можно применить формулы для многоканальной марковской системы массового обслужива­ния без блока ожидания M/ M/ c_k / c_k:

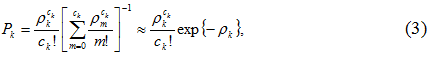
где ρ_k — вероятность того, что в транспортном средстве будет k пассажиров.

Из условия, что ρ_k < c_k (количество мест в транспортном средстве ниже среднего количества пассажиров, выбирающих данный маршрут), получена приближенная формула, т.е. транспортное средство должно хотя бы в среднем обеспечивать перемещение пассажира. На практике даже в часы пик должно выполняться соотношение [3]:

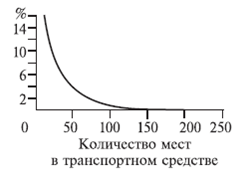
Проверим точность (3) на примере при выполнении равенства в формуле (4) с помощью рис. 1.

Рис. 1 - Относительная погреш­ность формулы (3).

Для автобусов особо малого класса формула (3) не точна, однако уже для автобусов малого класса ПАЗ-32054 при общем количестве мест 42 погрешность составляет менее 5 %, а для авто­бусов большого класса (Волжа­нин-5270) — менее 1 %.

Прибыль транспортного оператора, обслуживающего маршрут k:

 

При подстановке (3) получим

Необходимо ввести показатель с_f — ущерб от отказа в обслуживании пассажира городским пасса­жирским транспортом для учета интересов пассажиров.

Потери системы «город»  можно вычислить по формуле:

Отметим, что (5) и (6) не являются выпуклыми вверх и вниз соответственно при всех значениях параметров. Поэтому вопрос о существовании равновесия Нэша или поиска глобального максимума при решении (6) остается открытым.

Численный пример

Пусть на одном маршруте интенсивность по­тенциального пассажиропотока составляет λ. При отказе в обслу­живании пассажир не использует данный маршрут для передвиже­ния. Интенсивность потока транспорта на маршруте — µ. Макси­мальная пассажировместимость — с, себестоимость выполнения одного рейса — α, ущерб городской среде — δ за рейс.

Упростив (5), получим прибыль городского пассажирского транспорта на данном маршруте:

Потери системы «город» исходя из (6) составят

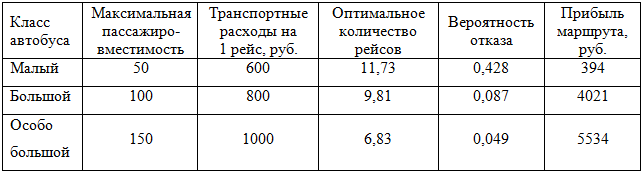
Рассмотрим решение (7) и (8) при следующих данных: стоимость пассажиро-часа γ - 50 руб., потери пассажиров при от­казе в обслуживании с_f - 50 руб., стоимость проезда β - 13 руб. Выберем три класса автобусов, обслуживающих данный маршрут, которые отличаются по пассажировместимости, транспортным расходам и ущербу городской среде (табл. 1, 2).

Результаты оптимизации показывают, что использование авто­бусов особо большой вместимости эффективно при данной ин­тенсивности пассажиропотока. Это связано с тем, что у автобусов малой вместимости высока вероятность отказа в обслуживании (0,428). Отметим, что положительная прибыльность автобусов малого класса достигается при стоимости проезда более 13 руб. , большого класса — при 9 руб. , а особо большого — даже при 7 руб.

Таблица 1 - Параметры и решение задачи (7)

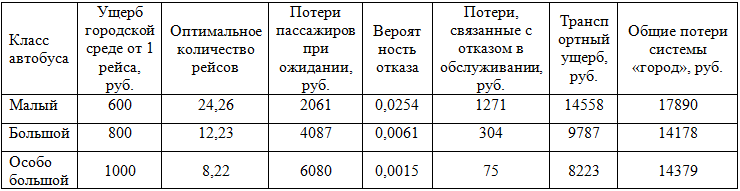
Таблица 2 - Параметры и решение задачи (8)

Для системы «город» наиболее эффективно использовать авто­бусы большого класса. При этом вероятность отказа значительно ниже, а количество рейсов выше, чем при решении (7). Исполь­зование же автобусов малого класса неэффективно.

Литература

1. Баламирзоев А.Г., Баламирзоева Э.Р., Курбанов К.О., Гаджиева А.М. Оптимизация одного вида общественного транспорта в городской среде// Фундаментальные исследования. – 2014. – № 11 (3). – С. 499-503.
2. Семенова О.С. Проверка адекватности методики расчета оптимальной интенсивности движения городского пассажирского транспорта Междуреченска/ М.Е.Корягин, О.С.Семенова//Вестн.Кузн.техн.ун-та.-2008.-№2.-С.139-142.
3. Шульга Ю.Н. Обобщение формулы Полячека-Хинчина для объемных стохастических сетей/ Ю.Н.Шульга// Автоматика и телемеханика.- 1989.-№ 3.-С.84-98.

References

1. Balamirzoev A.G., Balamirzoeva E.R., Kurbanov K.O., Gadzhieva A.M. Optimizaciya odnogo vida obshhestvennogo transporta v gorodskoj srede//Fundamentalnye issledovaniya. – 2014. – № 11 (3). – s. 499-503.
2. Semenova o.s. Proverka adekvatnosti metodiki rascheta optimalnoj intensivnosti dvizheniya gorodskogo passazhirskogo transporta mezhdurechenska/ M.E.Koryagin, O.S.Semenova//vestn.kuzn.texn.un-ta.-2008.-№2.-s.139-142.
3. Shulga Yu.N. Obobshhenie formuly polyacheka-xinchina dlya obemnyx stoxasticheskix setej/ yu.n.shulga// avtomatika i telemexanika.- 1989.-№ 3.-s.84-98.