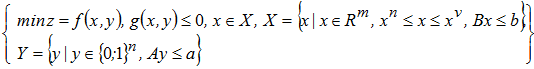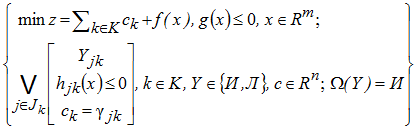Наши журналы
Опубликовать статью Вход и регистрация
Расширенный поиск
Разделы статьи

МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ И СИНТЕЗ ПОТОЧНЫХ ТЕХНОЛОГИЧЕСКИХ СХЕМ В НЕФТЕПЕРЕРАБОТКЕ

Научная статья
Бычков Ю.С.
Анкудинов Г.И.
Выпуск: № 9 (40), 2015
Опубликована:
2015/10/15
PDF

Бычков Ю.С.1, Анкудинов Г.И.2

1Магистр, 2Профессор, Национальный минерально-сырьевой университет «Горный»

МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ И СИНТЕЗ ПОТОЧНЫХ ТЕХНОЛОГИЧЕСКИХ СХЕМ В НЕФТЕПЕРЕРАБОТКЕ

Аннотация

В статье рассмотрена - возможность повышения технико-экономической эффективности технологических схем нефтепереработки на основе формализации знаний о предметной области и автоматизации задач структурного синтеза с использованием математического программирования. Практическое применение заключается в эффективном использовании сырьевых ресурсов России, а именно – повышении эффективности технологических процессов нефтепереработки и в конечном счет увеличении прибыли.

Ключевые слова: нефтепереработка, программирование, синтез.

Bychkov Y.S.1, Ankudinov G.I.2

1Masters, 2Professor, National University of mineral resources "Mountain"

MATHEMATICAL PROGRAMMING AND SYNTHESIS FLOW SEQUENCE IN OIL REFINING

Abstract

The article deals with - the ability to increase the technical and economic efficiency of technological schemes of oil refining on the basis of formalization of domain knowledge and automation problems of structural synthesis using mathematical programming. Practical application is the efficient use of natural resources of Russia, namely - improving the efficiency of technological processes of oil refining and ultimately increase profits.

Keywords: refining, programming, synthesis.

Рассмотрим применение математического аппарата целочисленного и смешанного (дискретно-непрерывного - ДНП) программирования к синтезу поточных схем технологических процессов [1, 2]. Задача ДНП может быть записана в общем виде

03-09-2015 13-39-33

где x - вектор непрерывных параметров решения; y - вектор логических параметров решения; f - целевая функция, выражающая интегральную технико-экономическую оценку решения; X - область  допустимых значений непрерывных параметров; g и h - векторы функций-ограничений, зависящих как от непрерывных, так и дискретных параметров.

Вычислительная сложность задачи (1) определяется как размерностью m и n пространств непрерывных и двоичных переменных соответственно, так и видом функций  f, g и h. Каждая двоичная (псевдобулева) переменная yi вектора-решения 03-09-2015 13-40-01 представляет соответствующий структурный элемент ei из множества структурных элементов 03-09-2015 13-40-51 конкретной задачи.

В задачах структурно-параметрического синтеза в состав функций  входят линейные функции-ограничения 03-09-2015 13-41-06, определяющие множество альтернативных вариантов элементного состава решений. Эти функции можно представить также в виде матричного неравенства Ay≤a, где A и a - матрица и вектор коэффициентов, соответственно. Каждый альтернативный вариант – это некоторое подмножество η множества E. Предполагается, что имеется информация о входах и выходах каждого элемента множества E, позволяющая установить связи между элементами  η и внешней средой.

Методы решения линейных задач дискретно-непрерывного программирования (ЛДНП)

03-09-2015 13-42-20

достаточно хорошо разработаны. В XX веке исследованию методов решения задач линейного и нелинейного программирования посвящены работы Е.Г. Гольдштейна, Л.В. Канторовича, Д.Б. Юдина, Г. Данцига, Е. Балаша и других авторов [3-7]. В приложении к структурно-параметрическому синтезу поточных схем задачи дискретно-непрерывного нелинейного программирования (НЛДНП) принимают вид

03-09-2015 13-42-38

Трудности «арифметизации» правил построения альтернативных вариантов на  основе псевдобулевых переменных привели авторов [1, 2] к необходимости использования аппарата логики высказываний, т.е. к задачам линейного логико-непрерывного программирования (ЛЛНП) и задачам нелинейного логико-непрерывного программирования (НЛЛНП). Поскольку ограничения в задачах линейного программирования «наиболее естественно» формализуются в виде импликаций «если Y0, то Y1 или Y2 или … или Yn» , которые можно представить в виде дизъюнкций 03-09-2015 13-43-28

В работах [6, 7] введено понятие «дизъюнктивного программирования».  Необходимость дальнейшего совершенствования методов решения задач НЛДНП и НЛЛНП привели авторов [1, 6, 7] к модели «обобщенного дизъюнктивного программирования», которая имеет вид [5]

03-09-2015 13-43-42

В этой модели используются булевы переменные 03-09-2015 13-43-55, принимающие значения «истина» (И) или «ложь» (Л) и фиксирующие включение того или иного элемента множества  в искомое решение. Булева функция Ω(Y) выражает те же правила построения альтернативных вариантов, что и система псевдобулевых ограничений Ay≤a. Для построения Ω(Y)  знания о МАВ представляются сначала в виде обобщенной схемы (максиально-избыточной структуры [1-3], или суперструктуры). Целевая функция имеет составляющую f(x), зависящую от непрерывных переменных, и составляющую 03-09-2015 13-45-17, где 03-09-2015 13-45-30, причем 03-09-2015 13-45-38, если 03-09-2015 13-45-54, и 03-09-2015 13-46-10, если 03-09-2015 13-46-18.

В [1] приведены примеры решения задач синтеза технологических схем производства этилена, очистки воды, производства цемента, схем размещения скважин добычи нефти и перерабатывающих платформ, цепей поставок и размещения многопродуктового производства.

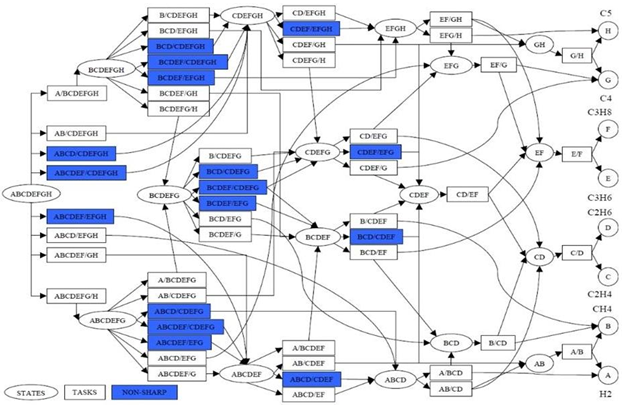
03-09-2015 13-46-31

Рис. 1 – Суперструктура, представляющая множество возможных вариантов технологического процесса этиленового завода

На рис. 1 представлена суперструктура, представляющая множество возможных вариантов технологического процесса этиленового завода. Сырье на входе – это смесь  водорода, метана, этана, этилена, пропана, пропилена, а также C4, C5 и C6.

Для каждой потенциальной функции разделения использованы такие блоки, дефлегматоры, мембраны, PSA, блоки физического и химического поглощения в дополнение к стандартным колонкам дистилляции и блокам охлаждения.

Суперструктура на рис. 1 содержит 53 операционных блока, включая такие блоки, как A/B – блок охлаждения; C/D – chemical absorber; E/F –сплиттер; G/H – дебутанизатор; F/G - депропанизатор; D/E - деэтанизатор; AB/CD –дефлегматор.

Для решения задачи синтеза в [1] использована параметрическая модель, содержащая 5800 псевдобулевых переменных и 52700 ограничений. Задача поставлена как обобщенная задача дизъюнктивного программирования и затем сформулирована как задача смешанного нелинейного программирования. Для решения этой задачи посредством пакета DICOPT (CONOPT2/CPLEX) потребовалось 3 часа процессорного времени на машине Pentium-III. Экономический эффект составил 30 миллионов долларов, главным образом за счет сокращения затрат на охлаждение.

Системное проектирование предполагает сравнение альтернативных вариантов проектных решений из множества и выбор наилучшего по критериальным показателям − критериям  технического совершенства, экономичности, эффективности, экологичности, социальной значимости и т.д. Критериальные показатели должны быть измеримыми, то есть должна быть установлены соответствующие шкалы уровней совершенства, эффективности и  т. д. Количественное оценивание показателей предполагает использование соответствующей шкалы.

Литература

  1. Grossmann I.E. Advances in logic-based optimization approaches to process integration and supply chain management // Chemical Engineering: Trends and Developments, M.A. Galan and E. Del Valle, Ed. West Sussex: Wiley, 2005. P. 299-322.
  2. Quaglia A., Sarup B., Sin G., Gani R. Integrated Business and Engineering Framework for Synthesis and Design of Enterprise-Wide Processing Networks // Computers & Chemical Engineering, 2012. Vol. 38, P. 213-223.
  3. Гольштейн Е.Г. Об одном классе нелинейных экстремальных задач // ДАН СССР, 133, 1960, №3. С. 507-510.
  4. Канторович Л. В. Новый метод решения некоторых классов экстремальных задач // ДАН СССР, 28, 1940. С. 211-214.
  5. Канторович Л. В. Методы оптимизации и математические модели экономик // УМН, 25:5(155), 1970. С. 107–109.
  6. Balas E. Disjunctive Programming // Annals of Discrete Mathematics, 1979, Vol. 5. P. 3-51.
  7. Balas E. Disjunctive Programming and a Hierarchy of Relaxations for Discrete Optimization Problems //. SIAM J. Alg. Disc. Meth. 1985, Vol. 6. P. 466-486.

References

  1. Grossmann I.E. Advances in logic-based optimization approaches to process integration and supply chain management // Chemical Engineering: Trends and Developments, M.A. Galan and E. Del Valle, Ed. West Sussex: Wiley, 2005. P. 299-322.
  2. Quaglia A., Sarup B., Sin G., Gani R. Integrated Business and Engineering Framework for Synthesis and Design of Enterprise-Wide Processing Networks // Computers & Chemical Engineering, 2012. Vol. 38, P. 213-223.
  3. Gol'shtejn E.G. Ob odnom klasse nelinejnyh jekstremal'nyh zadach // DAN SSSR, 133, 1960, №3. S. 507-510.
  4. Kantorovich L. V. Novyj metod reshenija nekotoryh klassov jekstremal'nyh zadach // DAN SSSR, 28, 1940. S. 211-214.
  5. Kantorovich L. V. Metody optimizacii i matematicheskie modeli jekonomik // UMN, 25:5(155), 1970. S. 107–109.
  6. Balas E. Disjunctive Programming // Annals of Discrete Mathematics, 1979, Vol. 5. P. 3-51.
  7. Balas E. Disjunctive Programming and a Hierarchy of Relaxations for Discrete Optimization Problems //. SIAM J. Alg. Disc. Meth. 1985, Vol. 6. P. 466-486.