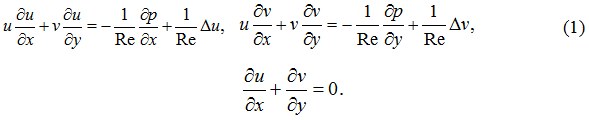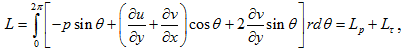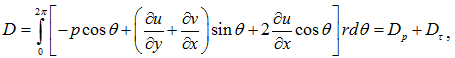ИССЛЕДОВАНИЕ ЭФФЕКТА МАГНУСА ПРИ ОБТЕКАНИИ КРУГОВОГО ЦИЛИНДРА ЛИНЕЙНЫМ ПОТОКОМ ВЯЗКОЙ ЖИДКОСТИ

Далабаев У.

Кандидат физ.-математических наук, доцент, Университет Мировой экономики и дипломатии

ИССЛЕДОВАНИЕ ЭФФЕКТА МАГНУСА ПРИ ОБТЕКАНИИ КРУГОВОГО ЦИЛИНДРА ЛИНЕЙНЫМ ПОТОКОМ ВЯЗКОЙ ЖИДКОСТИ

Аннотация

В статье численно исследованы гидродинамические параметры  обтекания вращающегося цилиндра в потоке вязкой несжимаемой жидкости в двумерной постановке.

Ключевые слова: подъемная сила, течение Куэтта, обтекание цилиндра.

Dalabayev U.

PhD in Physics and mathematics, associate professor, University of World Economy and Diplomacy

RESEARCH OF EFFECT OF MAGNUS AT THE FLOW OF THE CIRCULAR CYLINDER IN LINEAR FLOW

Abstract

In article hydrodynamic parameters of a flow of the rotating cylinder in a stream of viscous incompressible fluid in two-dimensional statement are numerically investigated.

Keywords: lift force, flow of Kuetta, cylinder flow.

В литературе изучению особенностей движения жидкости около кругового цилиндра, вращающегося с постоянной угловой скорости, посвящено много экспериментальных и численных исследований [1- 4 и литература в них]. Наиболее важным эффектом при вращении цилиндра в потоке вязкой жидкости является возникновение подъемной силы, действующей на цилиндр. Возникновение подъёмной силы наблюдается не только при вращении цилиндра, но и при обтекании неравномерным потоком. В работе [1] исследуется эффект Магнуса вращающегося цилиндра в линейном безграничным потоке нестационарным уравнениям вязкой жидкости в переменных функции тока – завихренность. Влиянию вращения цилиндра в равномерном потоке посвящена работа [2]. В работе [3] исследовано влияние вращения цилиндра вязкой жидкости в переменных функции тока – завихренность. На основе уравнения вязкой жидкости в естественных переменных исследовано вращения цилиндра в равномерном потоке в работе [4]. Влиянию вращения цилиндра на  пуазельовский поток посвящена работа [5].

Цель настоящей работы – определение гидродинамических характеристик при обтекании вращающегося кругового цилиндра на основе численного моделирования двухмерного ламинарного обтекания линейным потоком Куэтта рамках стационарного уравнения несжимаемой жидкости в естественных переменных.

Рис. 1 - Схема течения

Рассмотрим течение Куэтта (рис. 1) при входе в плоскопараллельный канал поступает линейный поток,  в котором расположен твердый цилиндр с осью,  перпендикулярной потоку. В зависимости от положения цилиндра по сечению значение подъемной силы будет различное. Среда считается несжимаемой, тогда двумерная безразмерная система уравнений Навье − Стокса имеет вид

Здесь Re – число Рейнольдса (Re=UH/ν, U – скорость подвижной границы, H – высота трубы, кинематическая вязкость, p=Re×P/ρU² – безразмерное давление). Ось x  направлена по нижней стенке, a ось y − перпендикулярно к ней.

На стенках канала ставятся условия прилипания: . На входе ставим линейный  поток u=y, v=0. В выходном сечении канала ставим мягкое условие:

На поверхности цилиндра ставятся условия прилипания с учётом скорости его вращения.

Для решения системы уравнений (1) при соответствующих граничных условиях применен алгоритм SIMPLE [5].

Расчет произведен в области  x∈[0,3], y∈[0,1],  за исключением области цилиндра, при различных значениях числа Рейнольдса Re и интенсивности вращения α ( α=ωН/U, где ω - угловая скорость вращения цилиндра). Центр частицы расположен в точке (1, у_с),  где значение у_с менялось от 0,1 до 0,9 с шагом 0,1.

В расчетах использована  согласованная неравномерная сетка 50x40 со сгущением вблизи поверхности цилиндра.   Когда расположение или радиус цилиндра меняется, сетка определяется заново.  До цилиндра приняли 10 узлов по х, сам цилиндр разделен на 10 узлов (на поверхности цилиндра выбраны 20 узлов) и после цилиндра  выбрали 30 узлов.

При конкретном числе Рейнольдса, радиусе и расположении цилиндра  расчеты осуществлялись вплоть до выполнения условия,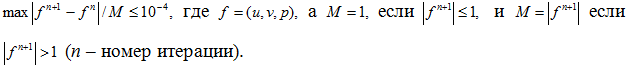

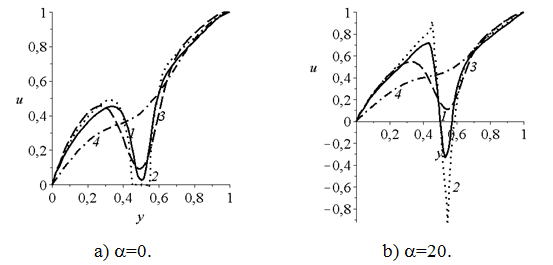
На рис. 2 приведены продольная скорость течения при различных сечениях трубы для Re=100 и α=0 и 20. При угловой скорости цилиндра вследствие прилипания вязкой жидкости существует слой жидкости, вращающейся вместе с цилиндром.

Рис. 2 - Распределение продольной скорости по сечениям: 1– x=0,9458; 2 –x=1,0150; 3 – x=1,1450; 4 – x=1,8056 (Re=100, центр цилиндра (1;0,5), радиус 0,05)

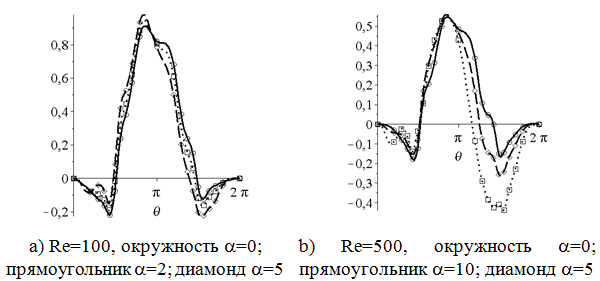
Распределение давления по поверхности цилиндра дано на рис. 3 (задняя критическая точка θ=0; и θ=2π).

Рис. 3 - Распределение давления по поверхности цилиндра (центр цилиндра (1;0,5), радиус 0,05)

По оси у отложена значения безразмерного давления , где Р₀ – давление в задней критической точке. Максимальные значения давления наблюдается вблизи передней критической точки в стороне верхней части, где продольная скорость больше. С увеличением угловой скорости минимум давлений увеличиваются по абсолютной величине при различных Re. Отметим также, что с увеличением Re асимметрия графика поверхностного давления увеличиваются, особенно это касается для нижней половине поверхности цилиндра. Значения давления, равной нулю, достигаются в верхней части цилиндра в одинаковых точках (≈π/2), а для нижней части цилиндра с увеличением a смещаются в сторону передней критической точке.

С увеличением Re, максимальное и минимальное значение давления по поверхности цилиндра уменьшается при соответствующих значениях a.

Исследовались также влияние расположения цилиндра по сечению трубы на подъемную силу с учетом вращения ее (рис. 4).

Возникновение подъёмной силы обусловлено не только вращением цилиндра. Подъёмная сила возникает также и при неподвижном цилиндре в неравномерном потоке.

Безразмерная подъемная сила на единицу длины цилиндра вычислена по формуле  – подъёмная сила)

где L_p представляет собой часть подъёмной силы, обусловленную силами давления и L_τ – часть подъёмной силы, обусловленной вязкими силами.

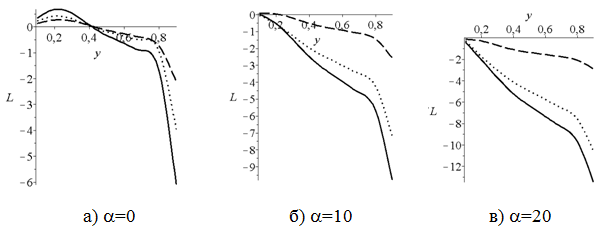
Рис. 4 приведены изменения подъёмной силы в зависимости от расположения цилиндра в трубе (сплошная линии – L, точки – L_p, пунктирные линии – L_τ).  На рис. 4а) представлены изменения подъёмной силы без учета вращения цилиндра; которая обусловлена из-за неравномерности потока. Вращение частицы вносит существенную корректировку на подъёмную силу (рис. 4б) и рис. 4в)). Во всех рассмотренных случаях, максимальные значения по модулю подъёмной силы возникают вблизи движущей стенки. При этом это значение в случае a=20 в два раза больше по сравнению с неподвижным цилиндром. Большой вклад в  подъемную силу осуществляется за счет сил давления – L_p. При этом, чем больше, a тем ощутим вклад интенсивности вращения на величину подъемной силы.

Рис. 4 - Влияние вращения цилиндра на подъёмную силу, Re=100, r=0,05.

Отметим что, с увеличением интенсивности вращения цилиндра против часовой стрелки точка с нулевом значением подъемной силы приближается к неподвижной стенки; и при дальнейшим росте такая точка отсутствует.

При этом увеличение число Рейнольдса приведет к приближению точки с нулевым значением подъемной силы к неподвижной стенке. Во всех рассмотренных случаях с увеличением скорости вращения имеет место возрастание подъёмной силы.

Исследовано также, влияние вращения цилиндра на силу сопротивления. Безразмерная сила сопротивления на единицу длины цилиндра вычислена по формуле

где D_p представляет собой часть силы сопротивления, обусловленную силами давления и D_τ – часть силы сопротивления, обусловленной вязкими силами.

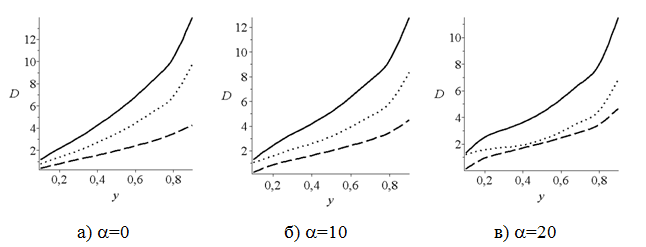
Рис. 5 - Влияние вращения цилиндра на силу сопротивления, Re=100, r=0,05.

Во всех рассмотренных случаях вклад сил давления на силу сопротивления больше чем сил трения. С увеличением a наблюдается тенденция к уменьшению силы сопротивления.

Литература

1. Fumio Yoshino and Tatsuo Hayashi. The Numerical Solution of Flow around a Rotating Circular Cylinder in Uniform Shear Flow// Bulletin of JSME, Vol. 27, No. 231, September 1984, pp. 1850-1857.
2. Stojkovic´, M. Breuer and F. Durst. Effect of high rotation rates on the laminar flow around a circular cylinder// Physics of fluids. 2002, Vol. 14, No 9, pp. 3160-3178.
3. Мазо А.Б., Моренко И.В. Численное моделирование вязкого отрывного обтекания вращающегося кругового цилиндр // Инженерно-физический журнал, т.79 №3, 2006, стр. 75-81
4. Редчиц Д.А., Гуржий А.А. Численное моделирование эффекта Магнуса при обтекании кругового цилиндра невозмущенным потоком вязкой жидкости// Прикладная механика. 2012, т. 14, № 1, стр. 63-71.
5. Далабаев У. Исследование характера подъемной силы, действующей на вращающей цилиндрической частицы в пуазейлевском потоке плоского канала.// Материалы международной научной конференции «Актуальные проблемы прикладной математики и информационных технологий – Аль-Хоразми 2012», Т. 1, стр.214-216
6. Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. М.: Энергоатомиздат, 1984

References

1. Fumio Yoshino and Tatsuo Hayashi. The Numerical Solution of Flow around a Rotating Circular Cylinder in Uniform Shear Flow// Bulletin of JSME, Vol. 27, No. 231, September 1984, pp. 1850-1857.
2. Stojkovic´, M. Breuer and F. Durst. Effect of high rotation rates on the laminar flow around a circular cylinder// Physics of fluids. 2002, Vol. 14, No 9, pp. 3160-3178.
3. Mazo A.B., Morenko I.B. Chislennoe modelirovanie vjazkogo otrivnogo obtekanija vrashayushegocja krukovogo chilindra// Injenerno-fizichiskie jurnal t.79 №3, 2006, s. 75-81
4. Redchic D.A., Gurjie A.A. Chislennoe modelirovanie effekta Magnusa pri obtekanii krukogo silindra nevozmushonnim potokom vjazkoe zhidkosti// Prikladnaja mehanika. 2012, t. 14, № 1, стр. 63-71.
5. Dalabaev U. Issledovanie haraktera pod’jomnoj sili deystvuyushej na vrashashnie cilindricheskoj chsastici na puzelovskom potoke ploskogo kanala// Materiali mezhdunarodnoj nauchnoj konferensii “Aktual’nie problemi prikladnoy matematiki i informasionnoj tehnologii – Alhorazmi 2012”, t. 1, s.214-216
6. Patankar S. Chislennoy metodi resheniya zadach teploobmena i dinamiki zhidkosti, M., Energoatomizdat, 1984