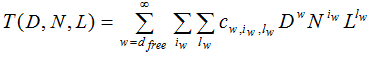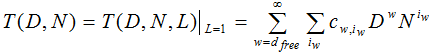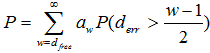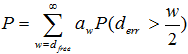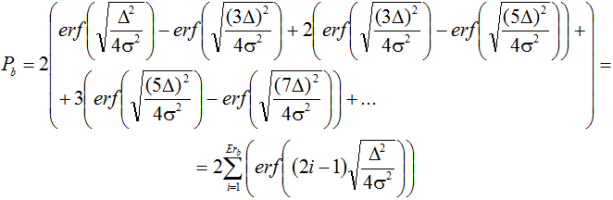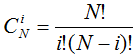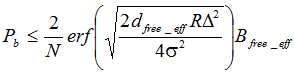ДИСТАНЦИОННЫЕ ХАРАКТЕРИСТИКИ ТУРБО-КОДОВ В КАНАЛАХ С ТАЙМЕРНЫМИ СИГНАЛАМИ
Захарченко Н.В. 1, Бектурсунов Д.Н. 2, Горохов Ю.С. 3, Талакевич Д.В. 4
1Доктор технических наук, 2Аспирант, 3Аспирант, 4Аспирант, Одесская национальная академия связи;
ДИСТАНЦИОННЫЕ ХАРАКТЕРИСТИКИ ТУРБО-КОДОВ В КАНАЛАХ С ТАЙМЕРНЫМИ СИГНАЛАМИ
Аннотация
На базе турбо-кодов проведен анализ основных параметров непрерывных наиболее полно отражающих свойства сверточных кодов.
Ключевые слова: турбо-коды, сверточные коды, компонентные коды.
Zakharchenko N.V. 1, Bektursunov D.N. 2, Gorohov Y.S. 3, Talakaevich D.V. 4
1Ph.D., 2Graduate, 3Graduate, 4 Graduate, Odessa National Academy of Telecommunications;
REMOTE DATA TURBO-CODES IN CHANNELS WITH TIMING SIGNALS
Abstract
On the basis of the turbo-code analyzes the basic parameters of continuous fully reflects the properties of convolution codes.
Keywords: turbo codes, convolutional codes, component codes.
Оценим эффективность непрерывных методов кодирования на примере турбо-кодов. Так как в качестве компонентных кодов в турбо-кодах используются свёрточные коды [1], то остановимся на определении их характеристик помехоустойчивости для каналов с таймерными сигналами. Одной из таких характеристик является понятие свободного расстояния свёрточного кода dfree, определяемое как минимальное кодовое расстояние между нулевым кодовым словом и всеми остальными кодовыми словами. Свободное расстояние используется для предварительного выбора сверточного кода и для оценки помехоустойчивости системы в целом [2].
Наиболее полное представление о дистанционных свойствах свёрточных кодов даёт порождающая функция свёрточного кода. В общем виде порождающая функция T(D,N,L) описывает полное множество путей, которые начинаются и заканчиваются в нулевом состоянии кода [3]
где степень w при формальной переменной D равна весу Хемминга данного пути; степень iw при формальной переменной N равна весу информационной последовательности, породившей этот путь; степень lw при формальной переменной L соответствует длине данного пути в тактовых интервалах; а коэффициент ![]() – соответствует количеству существующих путей с указанными параметрами, которые начинаются и заканчиваются в нулевом состоянии.
– соответствует количеству существующих путей с указанными параметрами, которые начинаются и заканчиваются в нулевом состоянии.
Порождающая функция позволяет рассчитать верхнюю границу вероятности ошибочного декодирования бита по критерию максимума правдоподобия. Поскольку при расчётах характеристик помехоустойчивости сверточного кода длина ошибочного пути не учитывается, то вместе с функцией T(D,N,L), применяется функция
где ![]() – число путей с общим весом w и информационным весом iw. Набор коэффициентов
– число путей с общим весом w и информационным весом iw. Набор коэффициентов ![]() , где w≥dfree называется спектром расстояний свёрточного кода.
, где w≥dfree называется спектром расстояний свёрточного кода.
Важной характеристикой так же является спектр информационных весов ![]() , где w∈[dfree, ∞). Он показывает суммарное количество ошибок, на выходе декодера максимального правдоподобия, когда вместо передаваемого пути выбирается ошибочный, находящийся от него на расстоянии w = d.
, где w∈[dfree, ∞). Он показывает суммарное количество ошибок, на выходе декодера максимального правдоподобия, когда вместо передаваемого пути выбирается ошибочный, находящийся от него на расстоянии w = d.
Расчёт вероятности ошибки производится на основании предположения, что ошибочные события случаются редко, что позволяет воспользоваться аддитивной верхней границей. Поскольку верхняя граница определяется выражением [3]
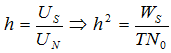 – для ФМ и
– для ФМ и ![]() для ЧМ – отношение сигнал-шум в канале, где: US – напряжение сигнала в канале; UN – среднее значение напряжения шума в канале; WS – мощность сигнала в канале (Вт); T – минимальная длительность импульса в канале (интервал Найквиста); N0 – односторонняя спектральная плотность мощности шума;
для ЧМ – отношение сигнал-шум в канале, где: US – напряжение сигнала в канале; UN – среднее значение напряжения шума в канале; WS – мощность сигнала в канале (Вт); T – минимальная длительность импульса в канале (интервал Найквиста); N0 – односторонняя спектральная плотность мощности шума; ![]() – СКЗ величины краевых искажений;
– СКЗ величины краевых искажений; ![]() – интервал времени между двумя соседними ЗММ.
– интервал времени между двумя соседними ЗММ.
Выражения [4]
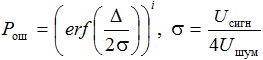 – для каналов с ФМ-2 или ЧМ-2,
– для каналов с ФМ-2 или ЧМ-2,
где ![]() – интеграл ошибок, i – среднее число ЗММ в кодовом слове, описывающая вероятность ошибки ТСК. Однако, связь между количеством таймерных сигналов, принятых с ошибкой, и количеством полученных ошибочных битов на выходе преобразователя ТСК в РЦК в общем случае не является однозначной. Вероятность ошибки битов зависит ещё и от манипуляционного кода, который используется такой СКК. Самый оптимальный случай построения МК для ТСК можно охарактеризовать тем, что ошибка в приёме одного ЗММ на интервал времени D приведёт к ошибке в одном бите РЦК, на интервал времени 2Δ приведёт к ошибке в двух битах РЦК и т.д. При этом однократная ошибка произойдет, если отклонение ЗММ превысит Δ/2, двойная ошибка произойдет, если отклонение ЗММ превысит 3Δ/2, тройная ошибка произойдет, если отклонение ЗММ превысит 5Δ/2. В таком случае вероятность ошибки бита на выходе демодулятора ТСК с оптимальным МК можно описать выражением
– интеграл ошибок, i – среднее число ЗММ в кодовом слове, описывающая вероятность ошибки ТСК. Однако, связь между количеством таймерных сигналов, принятых с ошибкой, и количеством полученных ошибочных битов на выходе преобразователя ТСК в РЦК в общем случае не является однозначной. Вероятность ошибки битов зависит ещё и от манипуляционного кода, который используется такой СКК. Самый оптимальный случай построения МК для ТСК можно охарактеризовать тем, что ошибка в приёме одного ЗММ на интервал времени D приведёт к ошибке в одном бите РЦК, на интервал времени 2Δ приведёт к ошибке в двух битах РЦК и т.д. При этом однократная ошибка произойдет, если отклонение ЗММ превысит Δ/2, двойная ошибка произойдет, если отклонение ЗММ превысит 3Δ/2, тройная ошибка произойдет, если отклонение ЗММ превысит 5Δ/2. В таком случае вероятность ошибки бита на выходе демодулятора ТСК с оптимальным МК можно описать выражением
где Erb – наибольшая кратность ошибки РЦК. При Δ/σ=2 подкоренное выражение в интеграле ошибок равно 1. При этом вероятность однократной ошибки из-за смещения одного ЗММ составит 0,31, двукратной составит 0,0054, трёхкратной – 1,72×10-6, четырехкратной – 2,06×10-11. Таким образом, однократные ошибки в этом случае составляют 98,33%, двукратные из-за смещения одного ЗММ составляют 1,67%, остальные – пренебрежимо малы.
При этом ошибка при анализе быстро уменьшается с ростом отношения Δ/σ. Уже при Δ/σ=3 вероятность однократной ошибки 0,133, а двукратной 1,36·10-5, что составляет около 99,99% и 0,01% от всех ошибок соответственно.
Кроме собственно компонентных кодов, в качестве которых в составе турбо-кода используются рекурсивные систематические свёрточные коды, в составе турбо кода также используется перемежитель. В этой связи полезным для анализа является понятие равномерного перемежителя [2]. Равномерный перемежитель, это абстрактное устройство, которое с вероятностью ![]() отображает входную последовательность длины N символов веса i в выходную последовательность того же веса. Здесь в знаменателе дроби число сочетаний из N по i
отображает входную последовательность длины N символов веса i в выходную последовательность того же веса. Здесь в знаменателе дроби число сочетаний из N по i
Дистанционные свойства и характеристики декодирования турбо-кода с использованием равномерного перемежителя являются математическим ожиданием характеристик полного ансамбля турбо-кодов с длинной блока N [3] (полное число кодов с длинной блока N равно N!). При этом характеристики турбо кода с детерминированным перемежителем могут быть, как лучше, так и значительно хуже характеристик кода с равномерным перемежителем.
В этом случае аддитивная верхняя граница вероятности ошибки бита в ТСК защищённой помехоустойчивым кодом выражается следующим образом
где N – глубина перемежения; Bfree_eff – эффективное количество ошибочных битов, возникающих на выходе турбо-декодера в результате действия помехи (в лучшем случае 1 бит); dfree_eff – эффективное свободное расстояние турбо-кода.
Полный вес Хемминга d какой-либо последовательности на выходе турбо-кода можно представить в виде трёх компонентов
где w – вес последовательности на систематическом выходе, а z1 и z2 веса последовательностей на выходе первого и второго компонентных кодов соответственно. Минимальный вес на выходе каждого компонентного кода не превышает величины
Следовательно, эффективное свободное расстояние кода вычисляется следующим образом:
Если в составе ТК используются перфорированные компонентные коды, то и перфорации подвергаются только соответствующие выходы компонентных кодов, что вызывает уменьшение dfree_eff, вследствие уменьшения величины zmin. В табл. 1 ниже указаны предельные величины dfree_eff в зависимости от относительной скорости турбо-кода и длины кодового ограничения его компонентных кодов.
Таблица 1 - Зависимость эффективного свободного расстояния турбо-кода от его относительной скорости и длины компонентных кодов.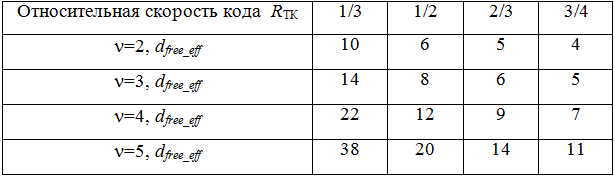
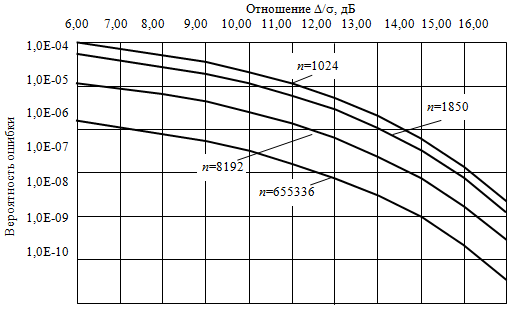
Для примера на рис. 1 построена зависимость верхнего предела ошибки для ν=2 RТК1 = 1/3 и RТК2 = 1/2 как функция отношения Δ/σ.
Рис. 1 - Верхний предел вероятности ошибки для n=2 RТК = 1/3
Литература
- Варгаузин В.А., Протопопов Л.Н. Турбо-коды и итеративное декодирование: принципы, свойства, применение // ТелеМультиМедиа №4, 2000, С. 33-45
- Помехоустойчивость и эффективность систем передачи информации. / А.Г. Зюко, А.И. Фалько, И.П. Панфилов, В.Л. Банкет, П.В. Иващенко; Под ред. А.Г. Зюко. – М.: Радио и связь, 1985. – 272 с.
- Басов В.Е. Эффективность совместного использования многопозиционных сигналов и свёрточных кодов. – Дис. канд. техн. наук.: 05.12.02 Одесса, 2006, 208 с.
- Захарченко Н.В. Басов В.Е. Эффективность компенсации избыточности кода при использовании таймерных сигналов // Зб. наук. пр. Моделювання та інформаційні технології: – Випуск 31. – Київ, 2005. – С. 6-13.
References
- Vargauzin V.A., Protopopov L.N. Turbo codes and iterative decoding: principles, properties, application // TeleMultiMedia №4, 2000, p.33-45
- Immunity and effectiveness of information transfer. / A.G. Zyuko, A.I. Falco, I.P. Panfilov, V.L. Banket, P.V. Ivashchenko; Ed. A.G. Zyuko. - M .: Radio and Communications, 1985. - 272 p.
- Basov V.E. The effectiveness of the sharing of multi-position signals and convolutional codes. - Dis. cand. tehn. Sciences .: 05.12.02 Odessa, 2006, 208 p.
- Zakharchenko N.V. Basov V.E. The effectiveness of compensation redundancy code using the timing signals // ST. Sciences. pr. Modeling and Information Technologies – Issue 31. - Kiev, 2005. - p. 6-13.