ИСПОЛЬЗОВАНИЕ ОБОБЩЕННЫХ ГАУССОВЫХ НЕЧЕТКИХ ЧИСЕЛ ПРИ ОПТИМИЗАЦИИ СЕТЕВОГО ГРАФИКА

Черменев Д.А.

Аспирант, Воронежский государственный технический университет

ИСПОЛЬЗОВАНИЕ ОБОБЩЕННЫХ ГАУССОВЫХ НЕЧЕТКИХ ЧИСЕЛ ПРИ ОПТИМИЗАЦИИ СЕТЕВОГО ГРАФИКА

 Аннотация

В статье рассматривается подход к оптимизации сетевого графика, когда продолжительности работ задаются в форме обобщенных гауссовых чисел, содержащих ряд параметров, которые позволяют настроить информационную среду задачи на конкретного пользователя.

Ключевые слова: нечеткое гауссово число, сетевой график, оптимизация

Chermenev D.A.

Postgraduate student, Voronezh State Technical University

USING GENERALIZED GAUSSIAN INTEGERS FOR OPTIMIZATION OF NETWORK SCHEDULE

The paper discusses an approach to the optimization of network schedule when the duration of the work are given in the form of generalized Gaussian numbers containing the number of options that allow you to customize the information environment of the problem to a specific user.

Keywords: Gaussian fuzzy number, network schedule, optimization

При управлении проектами часто возникает задача оптимизации того или иного критерия. Рассмотрим задачу оптимизации времени выполнения проекта.

Пусть задан директивный срок 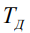 завершения всего комплекса работ. Необходимо уменьшить 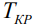, то есть составить более напряженный план, что может быть достигнуто за счет сокращения продолжительности той или иной критической работы.

Стремление перестроить план наилучшим образом приводит к задаче определения 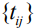 вида

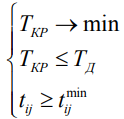                                                                                                      (1)

где 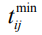 - нижняя граница продолжительности работы, определяемая нижними границами ее выполнения. В качестве признака оптимальности сетевого графика рассмотрим условие

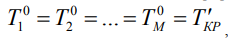                                                                      (2)

где 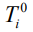 - длина i-го пути из исходного события в завершающее, полученная в результате оптимизации;  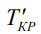- новое критическое время; M- количество таких путей.

В большинстве случаев время выполнения работ невозможно точно определить, т.е. имеет место неопределенность.

Для времени выполнения операции 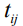 предлагается использовать обобщенные Гауссовы нечеткие числа (L-R)-типа с функцией принадлежности вида:

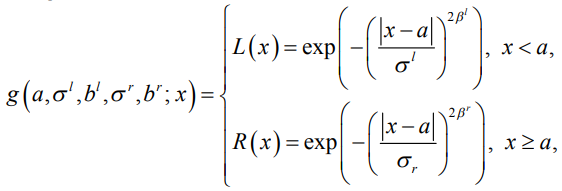                 (3)

где 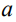- модальное значение,  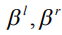- параметры формы для функций  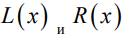соответственно,  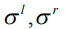- параметры «ширины» нечеткого числа соответственно слева и справа от модального значения.

Так как функция принадлежности является выпуклой, то 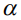-срез представляет собой интервал или отрезок в зависимости от того является он строгим или слабым. В дальнейших рассуждениях будем использовать слабые 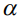-срезы, границы которых определяются следующим образом:

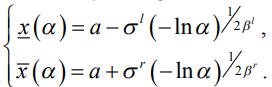
Обозначив 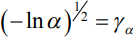, получим

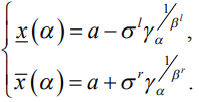                                                                 (4)

Для 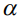-среза можно вычислить среднее значение

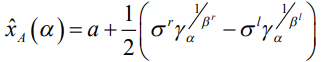                                                 (5)

Данное значение реализует функцию дефаззификации.

Полученное значение будем использовать в качестве времени выполнения 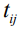 при оптимизации сетевого графика.

Продолжительность работы 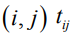 есть функция от средств, направляемых на ее выполнение, и носит линейный характер [1].

Пусть 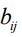 - величина средств, выделяемых на выполнение работы 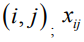- величина средств, переносимых с работы 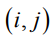, тогда 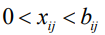. В общем случае 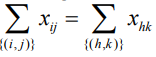.Для уменьшения критического пути средства переносятся с некритических работ, обладающих ненулевым свободным резервом, на критические. Средства 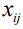, вложенные в критическую работу 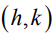, приводят к увеличению времени выполнения работы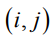

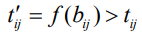
и к уменьшению выполнения работы (h, k)

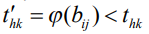
Формулы для пересчета новых продолжительностей работ 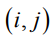 и 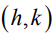 имеют вид:

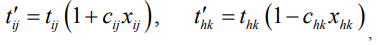                    (6)

где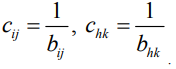

Перенос средств с некритической работы 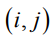 на критическую работу  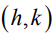влечет за собой изменение длин путей

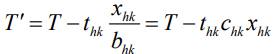                                                             (7)

длина пути, содержащего работу 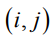, увеличится и составит

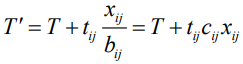                                                                     (8)

В процессе перераспределения средств необходимо соблюдать условие

.

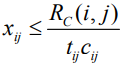Оптимизация сетевого графика состоит в последовательном переносе средств с некритических работ на критические до тех пор, пока все пути из исходного события в завершающее не станут критическими с одинаковой длиной, равной новому критическому времени.

Рассмотрим сетевой график, представленный на следующем рисунке.

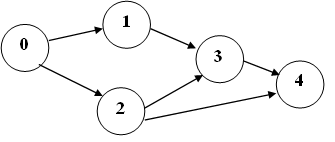
Рисунок 1 – Пример сетевого графика

Продолжительности работ заданы в виде обобщенных гауссовых чисел, параметры которых представлены в табл. 1.

Табл. 1 – Значения параметров функции принадлежности продолжительностей работ

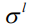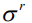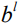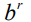0-1	5	2	3	3	0,3
0-2	7	4	3	0,5	0,9
1-3	4	1	2	1	4
2-3	3	1	1	2	0,5
2-4	9	3	5	2,5	0.7
3-4	6	2	4	5	2

 

Табл. 2 – Временные характеристики сетевого графика при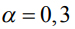

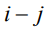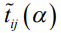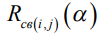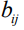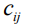0-1	6	0	4	0,25
0-2	6,25	0	2	0,5
1-3	4,47	0	3	0,333
2-3	3,07	1,15	5	0,2
2-4	10,29	1	1	1
3-4	7,07	0	2	0,5

Найдем все пути из исходного события сети в завершающее событие.

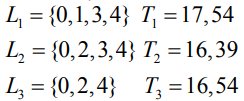
Таким образом критический путь равен .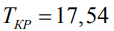

Определим резервы всех путей: .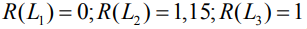

Ближайшим к критическому пути является путь 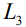. Перенесем средства с некритической работы {2,4} на критическую работу {0,1}:

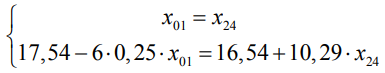
Откуда 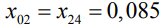. Найдем новые продолжительности работ и новый критический путь: 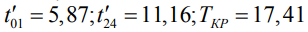. Выполняя дальнейшие вычисления по алгоритму в итоге получим значения для продолжительностей работ, представленные в табл. 3, и критических путей.

Табл. 3 – Итоговые времена работ

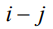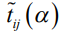0-1	5,21
0-2	6,25
1-3	4,47
2-3	3,43
2-4	10,5
3-4	7,07

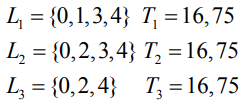
Таким образом, рассмотрена задача оптимизации сетевого графика с продолжительностями работ в виде обобщенных Гауссовых нечетких чисел. Получены продолжительности работ сетевого графика, в котором все пути являются критическими, следовательно данный график является оптимальным по времени выполнения работ.