СВЯЗЬ ФИЗИЧЕСКИХ СВОЙСТВ С КРИСТАЛЛОГРАФИЧЕСКИМИ ПАРАМЕТРАМИ ИОННЫХ КРИСТАЛЛОВ

Хентов В.Я.

Профессор, доктор химических наук, Южно-Российский государственный политехнический университет имени М.И. Платова

СВЯЗЬ ФИЗИЧЕСКИХ СВОЙСТВ С КРИСТАЛЛОГРАФИЧЕСКИМИ ПАРАМЕТРАМИ ИОННЫХ КРИСТАЛЛОВ

Аннотация

Получены функциональные зависимости температуры Дебая для ряда шпинелей. Установлено, что зависимость относительной молекулярной массы от параметра решетки удовлетворительно описывается линейным уравнением. Показано сложное влияние кристаллографических параметров на плотность ряда шпинелей.

Ключевые слова: Температура Дебая, относительная молекулярная масса, параметр решетки, плотность шпинелей.

Khentov V.Ya.

Professor, Doctor of Chemistry, South-Russian State Technical University named after M. Platov

RELATIONSHIP OF PHYSICAL PROPERTIES WITH THE CRYSTALLOGRAPHIC PARAMETERS OF IONIC CRYSTALS

Abstract

Obtained functional dependence of the Debye temperature for a number of spinels. The dependence of the relative molecular mass of the lattice parameter is satisfactorily described by a linear equation. Revealed a complex effect of crystallographic parameters of the density of a number of spinels.

Keywords: Debye temperature, relative molecular mass, the lattice parameter, the density of spinel.

Известно, что некоторые кристаллографические параметры определяют физические свойства кристаллов. Одним из таких параметров является характеристическая температура Дебая, которая зависит от сил взаимодействия между частицами [1]. Для гетерогенных систем чрезвычайно важны поверхностные характеристики твердого тела. В этом случае динамические свойства поверхности твердого тела связаны с температурой Дебая [2]. Для простых веществ была обнаружена связь характеристической температуры Дебая с рядом физических и химических свойств. Оказалось, что с температурой Дебая связаны температура плавления и кипения, плотность, энтальпия плавления и испарения, теплоемкость, энергия связи элементов, коэффициент линейного теплового расширения, сжимаемость, объемный модуль упругости, параметр решетки, работа выхода электрона, энергия Ферми, энергия ионизации, стандартный электродный потенциал, энергия активации некоторых химических реакций разложения [3]. В работе [4] установлена связь энергии активации самодиффузии с температурой Дебая. Таким образом, собственная (предельная) частота упругих колебаний кристаллической решётки оказывает существенное влияние на физические и химические свойства твердого тела.

Поскольку дебаевская температура пропорциональна дебаевской частоте, т.е. обратно пропорциональна корню квадратному из массы атома, то между эффективной температурой Дебая θ_эфф и дебаевской температурой основного кристалла θ_крист существует связь [5]:

θ_эфф = (М/М^*)^0,5θ_крист,

где М – масса атома основной решетки, М^* – масса примесного атома.

Действительно, для простых веществ однотипных элементов такая связь имеет место. Например, для s-элементов I группы зависимость θ_эфф от М^0,5 удовлетворительно описывается полиномом 1 степени, но лучше полиномом 2 и особенно 3 степени. В (табл. 1) приведены функциональные зависимости температуры Дебая θ_эфф  s-элементов I группы [6] от корня квадратного из относительной молекулярной массы М^0,5.

Аналогичные зависимости получены для сложных химических соединений, в том числе и для соединений переменного состава, – SrTiO₄, BaTiO₃, KTaO₃, PbZr_0,65Ti_0,35O₃, BaBi_0,3Pb_0,7O₃, PbZr_0,95Ti_0,05O₃ (табл. 2).

 

Таблица 1 ‒ Уравнение регрессии; температура Дебая θ_эфф  (К); коэффициент корреляции R; стандартное отклонение CD; уровень значимости р

Уравнение регрессии	R	CD	р
θэфф = 10,329 ‒ 0,025М0,5	0,88	1,94	0,05
θэфф = 13,902 ‒ 0,087М0,5 + 1,584·10–4(М0,5)2	0,96	1,03	0,04
θэфф = 18,634 ‒ 0,23М0,5 + 0,001(М0,5)2 ‒1 ,974·10–6(М0,5)3	1,00	0,03	0,01

 

Таблица 2 ‒ Функциональные зависимости температуры Дебая θ_эфф  (К) для ряда шпинелей [7] от корня квадратного из относительной молекулярной массы М^0,5: коэффициент корреляции R, стандартное отклонение CD, уровень значимости р

Уравнение регрессии	R	CD	р
θэфф = 775,434 ‒ 28,257М0,5	0,82	68,35	0,04
θэфф = ‒808,599 + 180,457(М0,5)0,5 ‒ 6,648(М0,5)2	0,86	50,91	0,05
θэфф = ‒6640,656 + 1335,717(М0,5) ‒81,451(М0,5)2 + + 1,586(М0,5)3	0,93	45,70	0,11

 

Интересно, что для ряда шпинелей (NiFe₂O₄; ZnFe₂O₄; CoFe₂O₄; MgFe₂O₄; MnFe₂O₄; Fe₃O₄; Li_0,5Fe_2,5O₄; γ-Fe₂O₃; CuFe₂O₄; CdFe₂O₄; Mg_0,5Mn_1,5Cr_1,5; MnFe_1,5Cr_0,5,O₄; MnFeCrO₄; MnFe_0,5Cr_1,5O₄; MgAl₂O₄) [8] зависимость относительной молекулярной массы М от параметра решетки а удовлетворительно описывается линейным уравнением:

М= ‒1325,5 + 1851,7а (R = 0,79, p = 0,0008).

Однако прямой зависимости между таким физическим свойством, как рентгеновская плотность и параметром а установить не удалось (R = 0,43).

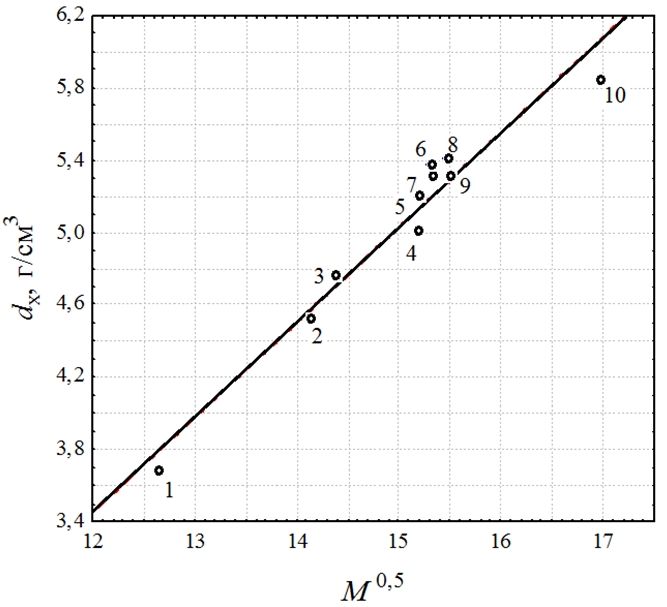
Для ряда сложных оксидов (NiFe₂O₄; ZnFe₂O₄; CoFe₂O₄; MgFe₂O₄; MnFe₂O₄; Fe₃O₄; Li_0,5Fe_2,5O₄; γ-Fe₂O₃; CuFe₂O₄; CdFe₂O₄) зависимость рентгеновской плотности [8] от М^0,5 идеально описывается полиномом первой степени d_x = ‒2,856 + 0,526M^0,5 (рис. 1). Плотность тесно связана с относительной молекулярной массой вещества.

 

Рис. 1. ‒ Зависимость рентгеновской плотности d_x (г/см³) от корня квадратного из относительной молекулярной массы M^0,5:

R = 0,98, p = 0,000001; (Соединения: 1 ‒ γ-Fe₂O₃; 2 ‒ MgFe₂O₄; 3 ‒ Li_0,5Fe_2,5O₄; 4 ‒ MnFe₂O; 5 ‒ Fe₃O₄, 6 ‒ NiFe₂O₄; 7 ‒ CoFe₂O₄; 8 ‒ CuFe₂O₄; 9 ‒ ZnFe₂O₄; 10 ‒ CdFe₂O₄)

 

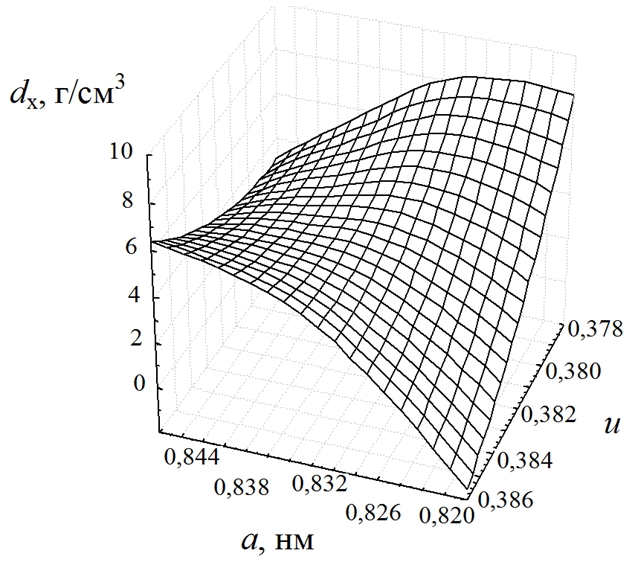
Рис. 2 ‒ Зависимость рентгеновской плотности d_x от параметра решетки а и кислородного параметра u

 

Зависимости физических свойств от кристаллографических параметров ионных кристаллов (параметра решетки a и кислородного параметра u) описываются нелинейными уравнениями. Обычно физическое свойство является функцией нескольких переменных. Например, рис. 2 демонстрирует зависимость рентгеновской плотности d_x от параметра решетки а и кислородного параметра u.

Как следует из рисунка, минимальную рентгеновскую плотность должно иметь вещество, характеризуемое минимальными значениями кристаллографических параметров а и u.