EFFECT OF EXTERNAL ELECTRIC FIELD WITH SPATIAL INHOMOGENEITY ON THE RECOVERY OF PHASE MEMORY OF THREE-LEVEL SYSTEM IN THE CASE OF STIMULATED PHOTON ECHO FORMATION
Низамова Э.И.1 , Нефедьев Л.А.2, Гарнаева Г.И.3, Сахбиева А.Р.4, Хакимзянова Э.И.5, Ахмедшина Е.Н.6
1 Старший преподаватель, 2 доктор физико-математических наук, профессор, 3кандидат физико-математических наук, доцент, 4 аспирантка, , 5 аспирантка, 6аспирантка, Казанский (Приволжский) федеральный университет
ВЛИЯНИЕ ВНЕШНЕГО ПРОСТРАНСТВЕННО НЕОДНОРОДНОГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ НА ВОССТАНОВЛЕНИЕ ФАЗОВОЙ ПАМЯТИ ТРЕХУРОВНЕВОЙ СИСТЕМЫ В СЛУЧАЕ ФОРМИРОВАНИИ СТИМУЛИРОВАННОГО ФОТОННОГО ЭХА
Аннотация
В данной работе исследованы условия восстановления фазовой памяти трехуровневой системы при наличии внешних пространственно неоднородных электрических полей в случае формирования стимулированного фотонного эха.
Ключевые слова: стимулированное фотонное эхо, трехуровневая система, параметр неэквидистантности спектра системы, внешнее пространственно неоднородное электрическое поле.
Nizamova E.I.1, Nefediev L.A.2, Garnaeva G.I.3, Sakhbieva A.R.4, Hakimzyanova E.I.5, Ahmedshina E.N.6
1senior lecturer, 2 Dr in Physics and mathematics, professor, 3 PhD in Physics and mathematics, associate professor, 4 postgraduate student, 5 postgraduate student, 6 postgraduate student, Kazan (Volga) Federal University
EFFECT OF EXTERNAL ELECTRIC FIELD WITH SPATIAL INHOMOGENEITY ON THE RECOVERY OF PHASE MEMORY OF THREE-LEVEL SYSTEM IN THE CASE OF STIMULATED PHOTON ECHO FORMATION
Abstract
In this paper the conditions for the restoration of phase memory of the three-level system in the presence of external spatially inhomogeneous electric fields in the case of the formation of the stimulated photon echo investigated.
Keywords: The stimulated photon echo, three-level system, parameter of nonequidistant system spectr, external spatially non-uniform electric field.
Когерентные переходные оптические явления типа фотонного эха предоставляют широкие возможности для оптической обработки информации, преобразования и усиления оптических импульсов, а также создания квантовой оптической памяти [1]. В последнее время большой интерес стали вызывать трехуровневые квантовые системы, в которых открываются новые возможности для управления квантовой когерентностью атомов [2-5]. В работах [6-8] рассматривалось влияние некоррелированности неоднородного уширения на различных энергетических переходах на формирование отклика стимулированного фотонного эха. Было показано, что эффективность запирания информации чрезвычайно чувствительна даже к незначительному изменению величины корреляции неоднородного уширения на различных частотных переходах. Существует возможность воздействовать на процесс формирования фотонного эха, подвергая многоуровневую систему взаимодействию с внешними пространственно неоднородными электрическими полями. В этом случае происходит нарушение частотно-временной корреляции неоднородного уширения резонансной линии на разных энергетических переходах на различных временных интервалах, что может привести к ситуации, когда информация не может проявиться в виде оптического отклика резонансной среды, то есть к «запиранию» эхо-голографической информации и разрушению фазовой памяти системы. В данной работе показано, что в отличие от двухуровневой системы, в трехуровневой системе восстановление фазовой памяти при формировании стимулированного фотонного эха (СФЭ) происходит при неодинаковых значениях градиентов внешних электрических полей, накладываемых между первым и вторым и после третьего возбуждающего импульса.
Основные уравнения
Для нахождения оператора эволюции U системы при ее возбуждении резонансным лазерным импульсом длительностью  в момент времени
в момент времени 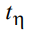 используем результаты работы [9]. Зная оператор эволюции U можно определить матрицу плотности после воздействия η-го лазерного импульса
используем результаты работы [9]. Зная оператор эволюции U можно определить матрицу плотности после воздействия η-го лазерного импульса
 (1)
(1)
Рассмотрим схему возбуждения стимулированного фотонного эха в трехуровневой системе по V – схеме.
В рассматриваемом случае гамильтониан системы можно представить в виде:
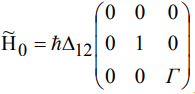 , где
, где  - параметр неэквидистантности спектра системы,
- параметр неэквидистантности спектра системы, 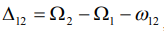 ,
, 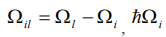 - энергия i-го уровня,
- энергия i-го уровня, 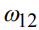 - частота лазерного излучения резонансного перехода 1-2.
- частота лазерного излучения резонансного перехода 1-2.
Напряженность электрического поля отклика найдем как
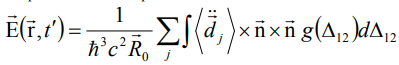 , (2)
, (2)
где 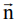 - единичный вектор в направлении наблюдения,
- единичный вектор в направлении наблюдения,  - функция распределения частот неоднородно уширенной линии резонансного перехода,
- функция распределения частот неоднородно уширенной линии резонансного перехода,  - радиус-вектор точки наблюдения,
- радиус-вектор точки наблюдения, 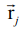 - радиус-вектор местоположения j-го оптического центра,
- радиус-вектор местоположения j-го оптического центра,  , а матричные элементы матрицы плотности после воздействия трех возбуждающих лазерных импульсов получены в работе [12].
, а матричные элементы матрицы плотности после воздействия трех возбуждающих лазерных импульсов получены в работе [12].
Воздействие внешних пространственно неоднородных электрических полей на резонансную систему атомов может влиять на воспроизводимость информации в откликах СФЭ. Следуя работам [6,7,8,9,10] будем считать, что воздействие неоднородных электрических полей приводит к дополнительным частотным сдвигам: 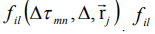 - частотный сдвиг за счет эффекта Штарка. В случае линейного эффекта Штарка во внешнем пространственно-неоднородном электрическом поле будем считать, что
- частотный сдвиг за счет эффекта Штарка. В случае линейного эффекта Штарка во внешнем пространственно-неоднородном электрическом поле будем считать, что 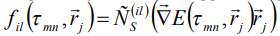 , где
, где  - время воздействия неоднородного электрического поля между первым и вторым возбуждающим импульсом,
- время воздействия неоднородного электрического поля между первым и вторым возбуждающим импульсом, 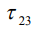 - время воздействия неоднородного электрического поля после третьего импульса,
- время воздействия неоднородного электрического поля после третьего импульса,  – постоянная. Величина
– постоянная. Величина 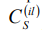 для кристалла LaF3: Pr3+ равна 100 Кгц/(В/см) [11].
для кристалла LaF3: Pr3+ равна 100 Кгц/(В/см) [11].
В этом случае пространственно-временная структура отклика СФЭ определится выражением аналогичным полученному в работе [12]:
 , (3)
, (3)
где

где,  – площадь η-го импульса,
– площадь η-го импульса, 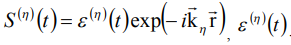 - временная форма объектного импульса,
- временная форма объектного импульса,  представляет спектр огибающей η-го импульса,
представляет спектр огибающей η-го импульса, 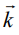 - волновой вектор.
- волновой вектор.
Восстановление фазовой памяти трехуровневой системы
Рассмотрим формирование стимулированного фотонного эха в системе трехуровневых оптических центров с неэквидистантными энергетическими уровнями ׀1›, ׀2›, ׀3› с энергиями ћΩ0, ћΩ1, ћΩ2 соответственно (рис.1). Уровни 1, 2, 3 соответствуют уровням энергии ионов Pr3+ в матрице LaF3. Переход 1 – 2 соответствует 3Н4→1D2 с длиной волны 600 нм, а переход 1 – 3 соответствует 3Н4→3Р0 с длиной волны 477 нм (параметр неэквидистантности спектра системы Г = 1,26). ωil(η) – несущие частόты излучения лазерных импульсов, резонансные соответствующим энергетическим переходам оптических центров.
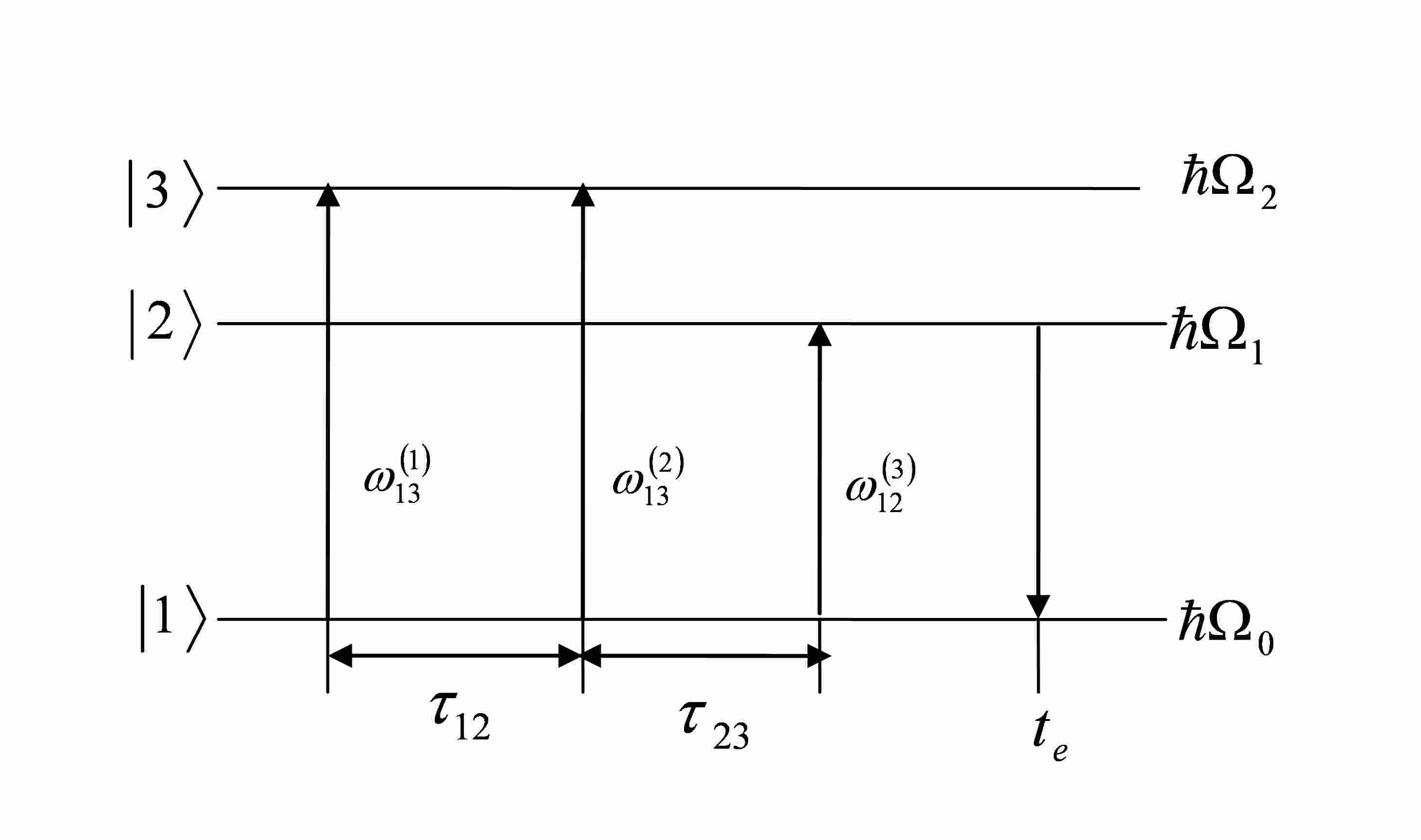
Рис.1. Спектр возбуждения СФЭ в трехуровневой системе. 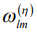 -несущая частота
-несущая частота  -го лазерного импульса на переходе,
-го лазерного импульса на переходе, 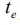 - время появления отклика СФЭ.
- время появления отклика СФЭ.
Нас будет интересовать интенсивность отклика стимулированного фотонного эха при различных значениях градиентов внешних пространственно неоднородных электрических полей, накладываемых на образец в интервалах времени между первым и вторым и после третьего возбуждающего импульса. На рисунке 2 приведен результат численного расчета выражения (3).

Рис. 2. Зависимость интенсивности отклика стимулированного фотонного эха, формируемого в трехуровневой системе от значений градиентов внешних пространственно неоднородных полей, Г=1,26.
Кроме того нами было рассмотрено формирование отклика стимулированного фотонного эха и при Г=1, то есть случай двухуровневой системы резонансных примесных центров. Результат расчета для этого случая приведен на рисунке 3.

Рис.3. Зависимость интенсивности отклика стимулированного фотонного эха формируемого в двухуровневой системе от значений градиентов внешних пространственно неоднородных полей, Г=1.
Заключение
Из анализа рисунков 2 и 3 следует, что в отличие от двухуровневой системы, в трехуровневой системе восстановление фазовой памяти происходит при неодинаковых значениях градиентов внешних электрических полей, накладываемых между первым и вторым и после третьего возбуждающего импульса, что проявляется в виде максимума интенсивности отклика стимулированного фотонного эха. Считая, что 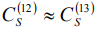 и Γ=1,26 (схема возбуждения на рисунке 1) максимум интенсивности наблюдается при отношении градиентов
и Γ=1,26 (схема возбуждения на рисунке 1) максимум интенсивности наблюдается при отношении градиентов  . Отметим, что для двухуровневой системы максимум интенсивности наблюдается при отношении градиентов
. Отметим, что для двухуровневой системы максимум интенсивности наблюдается при отношении градиентов 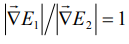 .
.
References
Kalachev A.A., Samartsev V.V., Coherent phenomena in optics. Kazan State University, Kazan. 2003. 280 pp.
Fleischhauer M., Lukin M.D. Entanglement of Atomic Ensembles by Trapping Correlated Photon States // Phys.Rev.Lett. 2000. V. 84. p. 4232 – 4235.
Tittel W., Afzelius M., Chaneliere Th., Cone R., Kroll S., Moiseev S.A., Sellars M. Photon-echo quantum memory in solid state systems // Laser & Photon. Rev., 2010. № 2. p. 244–267.
Нефедьев Л.А., Самарцев В.В. Цветная эхо-голография // Оптика и спектроскопия. 1987. Т. 62. № 3. С. 701-703.
Nefediev L.A., Rusanova I.A. Copying quantum information in a three-level medium with a phase memory // Laser physics. 2002. V.12. № 3. P. 1-5.
Нефедьев Л.А., Низамова Э.И., Тактаева С.В. Влияние некоррелированности неоднородного уширения на формирование переходных оптических процессов в многоуровневых системах // Оптика и спектроскопия. 2012. Т. 113. №2. C. 156-161.
Нефедьев Л.А., Гарнаева (Хакимзянова) Г.И. Корреляция неоднородного уширения и эффективность запирания информации в оптических эхо-процессор // Оптика и спектроскопия. 2005. Т. 98. №1. С. 41-45.
Нефедьев Л.А., Гарнаева (Хакимзянова) Г.И. Эффект «запирания» сигналов фотонного эха при многоканальной записи информации // Оптика и спектроскопия. 2008. Т. 105. № 6. С. 1007-1012.
Нефедьев Л.А., Гарнаева Г.И., Усманов Р.Г. Многоканальная запись информации на основе эффекта «запирания» сигналов фотонного эха // Оптический журнал. 2010. Т. 77. № 2. С. 27-29.
Нефедьев Л.А., Гарнаева (Хакимзянова) Г.И. Эффект «запирания» информации в оптических запоминающих устройствах на основе фотонного эха // Вестник ЧелГу. 2009. Выпуск 6 (физика). №25 (163). С. 13-22.
Mitsunaga M., Yano R., Uesugi N. Time- and frequency-domain hybrid optical memory: 1.6-kbit data storage in Eu3+:Y2SiO5 // Optics Letters. 1991. V. 16. P. 1890-1892.
Nefediev L.A., Sakhbieva A.R., Nizamova E.I. Determination of optimum conditions for reproducing information in optical echo processors // Journal of Russian laser research. 2013. V. 34. № 4. P. 355-359.
