ДИНАМИЧЕСКИЕ РЕАКЦИИ ПОДШИПНИКОВ БЫСТРО ВРАЩАЮЩЕГОСЯ ОСЕССИММЕТРИЧНОГО ТЕЛА, ЗАКРЕПЛЁННОГО С ПЕРЕКОСОМ

Баранов М.А.¹, Мухопад К.А.², Щербаков В.М.³;

¹ доктор физико-математических наук, профессор, Алтайский государственный технический университет; ² старший преподаватель, Алтайский государственный технический университет; ³ старший преподаватель, Алтайский государственный технический университет;

ДИНАМИЧЕСКИЕ РЕАКЦИИ ПОДШИПНИКОВ БЫСТРО ВРАЩАЮЩЕГОСЯ ОСЕССИММЕТРИЧНОГО ТЕЛА, ЗАКРЕПЛЁННОГО С ПЕРЕКОСОМ

Аннотация

Анализируются динамические реакции подшипников, на оси которых вращается тело произвольной осесимметричной формы, закреплённое так, что его ось симметрии образует произвольный угол с осью вращения.

Ключевые слова: осевая симметрия, вращение, силы инерции.

Baranov M. A.¹, Mukhopad K.A.², Shcherbakov V, M.³;

¹ PhD in Physics and mathematics, professor, Altay State Technical University; ² senior teacher, Altay State Technical University; ³ senior teacher, Altay State Technical University;

DYNAMIC CONSTRAINT FORSES OF BEARINGS OF QUICKLY ROTATING AXIS-SYMMETRICAL ASKEW FIXED BODY

Abstract

Dynamic constraint forces  of bearings, on axis of which rotate axis-symmetrical body are analyzed. Corner between symmetrical axis and rotation axis can be arbitrary.

Keywords: axial symmetry, rotation, inertia forces.

Работа современных механизмов и машин основана на вращении деталей, большинство из которых имеют осесимметричную или близкую к ней форму. Это колёса, шестерни, маховики, роторы, крыльчатки, турбины и многое другое. Технологии изготовления подобных деталей (токарные и карусельные станки, точное литьё, штамповка) вполне отработаны и обеспечивают их необходимую точность. При совпадении оси симметрии детали с осью её вращения реакции подшипников во время вращения остаются такими же, как и в статическом состоянии, то есть, компенсирующими лишь силу тяжести. Однако даже самое незначительное несовпадение этих осей приводит к возникновению дополнительных динамических реакций подшипников, обусловленных вращением. При больших угловых скоростях абсолютная величина этих сил может значительно превышать вес вращающейся детали и, в конечном счёте, стать причиной выхода из строя подшипников или механизма в целом. В этой связи предвидение динамических реакций подшипников в зависимости от формы и размеров детали, а также параметров её установки остаётся крайне актуальным. Смещение центра масс произвольного вращающегося тела на Δr_C относительно оси вращения приводит к возникновению главного вектора центробежных сил инерции 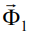. Выражение для модуля этого вектора является классическим

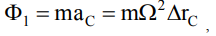                                          (1)

где m – масса вращающегося тела, а_С – модуль ускорения центра масс, Ω – угловая скорость. Произвольное осесимметричное тело представимо в виде следа, заметаемого одним из главных сечений тела (плоской фигурой) при его вращении вокруг некоторой оси z (оси симметрии), лежащей в плоскости сечения и не пересекающей его (рисунок 1).

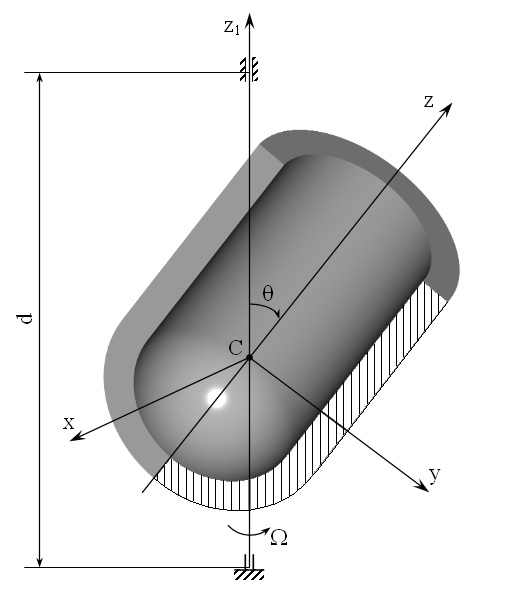
Рисунок 1. Разрез вдоль одного из главных сечений (показано штриховкой) осесимметричного тела, установленного на оси вращения z₁ с перекосом. θ – угол перекоса; Cz – ось симметрии; Cx – ось поворота тела на угол θ .

Рассмотрим случай, когда центр масс С тела находится на оси вращения z₁, а его ось симметрии z образует с ней угол θ. Ось z формально может быть совмещена с осью z₁ путём обратного поворота тела на угол θ вокруг оси Cx, проходящей через центр масс перпендикулярно выбранному главному сечению. Ось y проведём из центра масс перпендикулярно оси z в плоскости сечения. Полученная система координат Cxyz жёстко связана с вращающимся телом. Главный вектор сил инерции в этом случае равен нулю, а главный момент сил инерции отличен от нуля и направлен параллельно оси x. Точное аналитическое выражение проекции главного момента сил инерции на ось x имеет вид

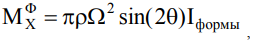                                          (2)

где ρ – плотность материала, Ω – угловая скорость, I_формы – интеграл формы, зависящий только от формы и размеров главного сечения:

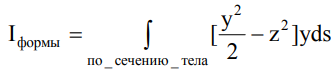  .                             (3)

Интегрирование в (3) проводится по площади сечения. ds – элемент площади. Строгий вывод этих соотношений приводится в [1, 2]. Реакции подшипников, обусловленные 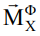 образуют пару сил, величины которых равны

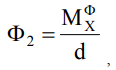                                                      (4)

где d – расстояние между подшипниками. Замечательно то, что влияние внешних (угловая скорость, угол перекоса) и внутренних (плотность материала, форма и размер тела) факторов на динамические реакции в (2) и, следовательно, в (4) представлено в виде независимых сомножителей, что существенно упрощает анализ и возможное предвидение этих сил. Характерной особенностью интеграла формы (3) является то, что он пропорционален пятой степени размеров тела. Это означает, что при сохранении плотности материала и внешних параметров вращения пропорциональное увеличение размеров тела, например, в 2 раза приведёт к увеличению динамических реакций в 32 раза.

       Допустимый интервал изменения угла θ от 0 (оси симметрии и вращения совпадают) до π/2 (оси перпендикулярны). В этом интервале углов sin(2θ) положителен. Поэтому знак проекции вращающего момента 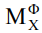 на ось x совпадает со знаком интеграла формы. При внимательном рассмотрении (3) видно, что если в сечении превалирует координата y то 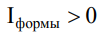, что характерно для сплюснутых тел. В этом случае возникает восстанавливающий момент сил инерции (М_восст), направленный вдоль оси x и, следовательно, стремящийся совместить ось симметрии с осью вращения. В сечении вытянутых тел превалирует координата z. Интеграл формы таких тел отрицателен. Возникающий при этом момент сил инерции направлен против оси x и стремится расположить ось симметрии перпендикулярно оси вращения. Такой момент является опрокидывающим (М_опр). Наиболее наглядно это на примере однородного цилиндра, показанного на рисунке 2.

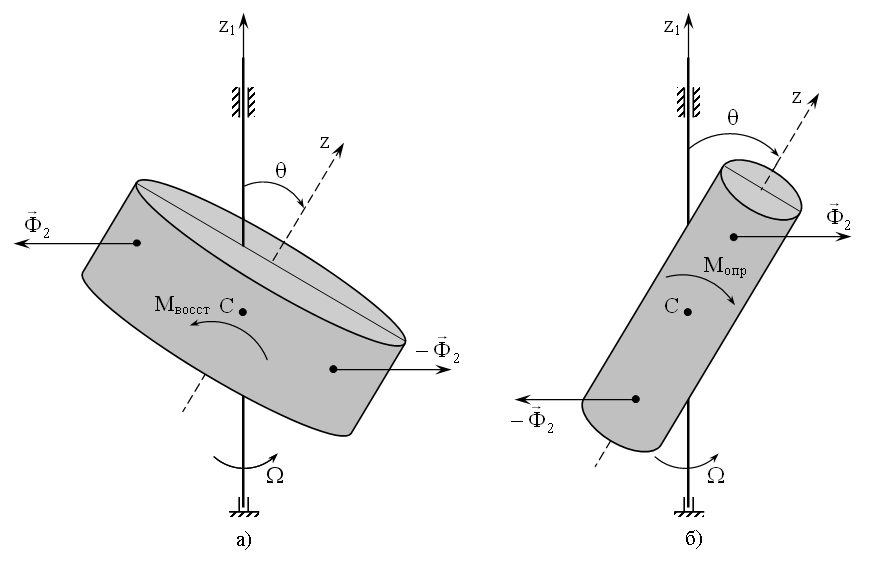
Рисунок 2. Восстанавливающий момент сил инерции (М_восст), действующий на сплюснутый (а) цилиндр и опрокидывающий момент (М_опр), действующий на вытянутый (б) цилиндр при их вращении вокруг оси z₁. 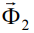 и -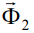 – главные векторы сил инерции, действующие на одну из половинок цилиндра.

 

       В соответствии с (3) пропорции размеров главного сечения можно подобрать так, что интеграл формы окажется нулевым. В этом случае, как момент сил инерции 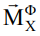, так и динамические реакции  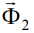останутся нулевыми при любых углах перекоса. Тело вращения с такими пропорциями правомерно назвать телом нейтральной формы. Тривиальным примером тела нейтральной формы является сферически симметричное тело.

Пример.

Из тонкостенной трубы диаметра D требуется изготовить маховик. Определить такую длину h заготовки трубы, чтобы при случайном перекосе осей маховика, допущенном при его изготовлении дополнительные динамические реакции подшипников не возникали. Массой спиц, связывающих маховик с осью пренебречь.

Для решения данной задачи получим выражение для интеграла формы и приравняем его к нулю. Начало координат необходимо совместить с центром масс маховика, который совпадает с его геометрическим центром. Элемент площади сечения удобнее всего выбрать в виде ds=dydz.

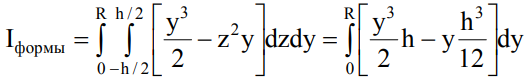              (5)

Пусть ΔR - малая, но не нулевая толщина трубы. Поскольку труба тонкая, то интегрирование по y имеет смысл заменить одним слагаемым при y=R

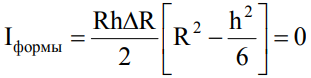                                    (6)

отсюда 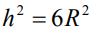 или .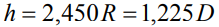

Момент сил инерции тел скомбинированных из материалов различной плотности представляется в виде суммы соответствующих моментов от их однородных частей. Для тел, имеющих выборки материала – диски с вырезами, крыльчатки, шестерни, колёса турбин и т.п. в выражениях (2) – (4) необходимо использовать значение плотности, усреднённой по заметаемому объёму. Естественно, что из-за отсутствия материала в выбранных объёмах усреднённая плотность окажется ниже плотности сплошного материала. В наиболее общем случае, когда ось вращения и ось симметрии являются скрещивающимися прямыми, реакции подшипников вынуждены компенсировать как главный вектор, так и главный момент сил инерции. При этом на одном из подшипников действие этих факторов компенсируется, а на другом усиливается.

Почти всегда динамические реакции подшипников являются вредными. При этом основная опасность заключается вовсе не в их большой величине, которая может в десятки и даже сотни раз превышать вес тела, а в том, что они знакопеременные. Меняя своё направление вместе с вращающимся телом Ω раз каждые π секунд, они приводят к эффекту отбойного молотка. Единственный способ борьбы этими силами заключается в точном изготовлении вращающихся деталей и в их точной установке.

В отличие от уже рассмотренных сил, от динамических реакций, обусловленных гироскопическим эффектом, невозможно избавиться никаким точным изготовлением деталей или их точной установкой. Но это и не страшно, поскольку таковые пропорциональны лишь первой степени угловой скорости и не знакопеременные.