ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ТЕМПЕРАТУРНЫХ ПАРАМЕТРОВ УДАРНОВОЛНОГО ТЕЧЕНИЯ В ГАЗОВЗВЕСИ В КАНАЛЕ С РАЗЛИЧНЫМИ ГРАНИЧНЫМИ УСЛОВИЯМИ
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ТЕМПЕРАТУРНЫХ ПАРАМЕТРОВ УДАРНОВОЛНОГО ТЕЧЕНИЯ В ГАЗОВЗВЕСИ В КАНАЛЕ С РАЗЛИЧНЫМИ ГРАНИЧНЫМИ УСЛОВИЯМИ
Аннотация
В статье представлена численная модель распространения ударной волны в канале из однородного газа в газовзвесь — взвесь дисперсных частиц в газе. Данная тематика является актуальной в связи с различными приложениями в технике. Несущая среда моделируется на основе системы уравнений Навье-Стокса. Математическая модель реализует континуальную методику моделирования динамики неоднородных сред — для каждой из компонент смеси решалась полная гидродинамическая система уравнений движения, учитывался обмен импульсом и теплообмен между компонентами смеси. Система уравнений динамики несущей среды и дисперсной фазы включает в себя уравнения непрерывности плотности, уравнения сохранения пространственных составляющих импульса несущей и дисперсной фазы, уравнения сохранения энергии. Уравнения математической модели решались явным конечно-разностным методом.
1. Введение
Так как математические модели процессов механики жидкости и газа являются нелинейными, для решения уравнений применяются численные методы. Среди гидродинамических процессов отдельно выделяют гидродинамические процессы с движением дисперсных сред. В отличие от гидро-газодинамики однородных сред , в неоднородной гидродинамике , , потоки сопровождаются взаимодействием компонент смеси , . В публикации разрабатываются трехмерные численные модели течений изотермальной вязкой ньютоновской многофазной. В работе с помощью методов гидродинамики неоднородных сред исследованы процессы взаимодействия ударных волн с газодисперсной взвесью. В статье также исследуется взаимодействие газа и дисперсных частиц. Рассматривались различные распределения концентрации дисперсных. В работе с помощью континуальной методики динамики неоднородных сред исследуются процессы взаимодействия газа и слоя дисперсных частиц. В исследовании рассматривались различные дисперсности частиц газовзвеси при взаимодействии газа и дисперсной завесы. В работе получены математические модели распространения ударных волн в газовзвеси в плане исследования технологических процессов горной промышленности. В статье численно моделируется ударно-волновые течения дисперсных сред.
Анализ работ, посвященных динамике неоднородных сред, демонстрирует, что в связи с проблемами горных и аэрокосмических технологий представляет интерес математическое моделирование ударноволновых течений газовзвесей.
2. Методы исследования
Для моделирования динамики газовзвесей на данный момент существует несколько подходов . Преимуществом математических моделей, разработанных в рамках континуальной концепции течений неоднородных сред является то, что такие математические модели могут более точно описывать динамику смесей с близкими массовыми долями компонент смеси, также такие модели позволяют моделировать течения с неоднородным распределением дисперсной фазы. В данной работе рассматривается течение, в котором происходит взаимодействие ударной волны, движущейся из однородного газа, с газовзвесью, дисперсная фаза которой имеет массовую долю близкую по значению с массовой долей несущей среды.
В данной работе моделируются процессы работы ударной трубы, заполненной однородным газом и газовзвесью, рассматриваются температурные поля несущей среды и дисперсной фазы для различных граничных условий скорости компонент смеси при моделировании течения газовзвеси в рамках континуальной модели динамики неоднородных сред. Математическая модель разработана на основе континуального подхода . Моделирование течения газа осуществлялось с двухмерным нестационарным уравнением Навье-Стокса для сжимаемой теплопроводной среды с учетом взаимодействия с дисперсной фазой, математическая модель описана в работе . Решение системы уравнений осуществлялось с помощью метода конечных разностей , .
Для улучшения численного решения применялась методика , .
Задавались два типа граничных условий. Для всех параметров несущей среды и дисперсной фазы задавались однородные граничные условия Неймана, для составляющих скорости газа и дисперсной фазы на границах расчетной области задавались либо однородные граничные условия Неймана, либо однородные граничные условия Дирихле. Такой выбор граничных условий связан с тем, что влияние граничных условий скорости на динамику потока может иметь существенное значение .
Для того чтобы определить работоспособность компьютерной программы, реализующей численную модель, было проведено сопоставление численных расчетов с физическим экспериментом . На рисунке 1 представлены сопоставления численных и экспериментальных результатов ударно-волновой динамики запыленных сред, изображены зависимости числа Маха фронта ударной волны от начального перепада давления. Сопоставляются данные, полученные в физическом эксперименте, проведенном в работе , c численными расчетами, проведенными в работе . Кривые 1 и 2 являются интерполяций экспериментальных и численных данных сплайном второго порядка . Результаты физического эксперимента хорошо согласуются с результатами расчетов численной модели, что демонстрирует её работоспособность.
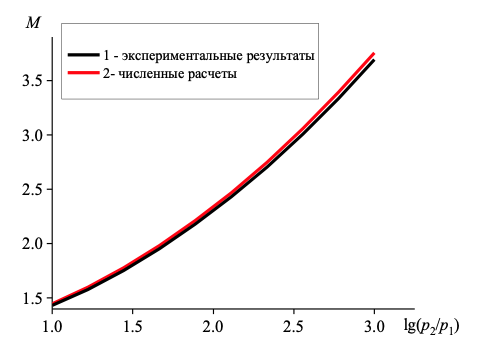
Рисунок 1 - Сопоставление числа Маха фронта ударной волны в газовзвеси
Примечание: кривая 1 построена обработкой экспериментов в работе [17], кривая 2 – результат численных расчетов
3. Результаты расчетов
В расчетах моделировалось течение в запыленной среде — воздухе с взвешенными твердыми частицами имеющими физическую плотность кварцевого песка. Параметры дисперсной фазы, физическая плотность материала — ρ10=2500 кг/м3, размер дисперсных включений — d=2 мкм, начальная объемная доля дисперсной фазы α0=0,001. Продольная длина канала — L= 1 м, размер канала в поперечном направлении — h=0,1 м. Количество узлов в х направлении — Nx=300, количество узлов в направлении у — Ny=60. Давление газа в камере высокого давления — р2=200 кПа, давление газа в камере низкого давления — р1=100 кПа – рисунок 2.
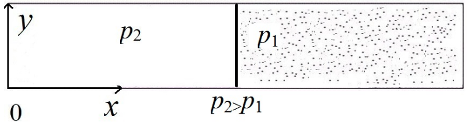
Рисунок 2 - Общая схема ударной трубы с газовзвесью
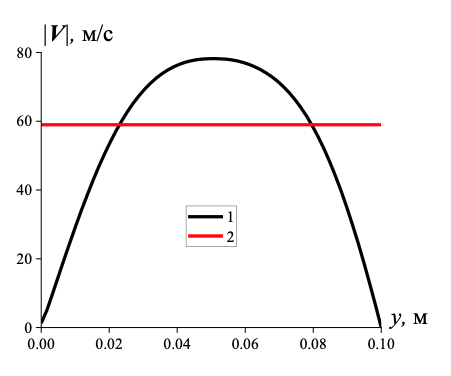
Рисунок 3 - Поперечное распределение модуля скорости газа для граничных условий Дирихле – 1, граничных условий Неймана – 2
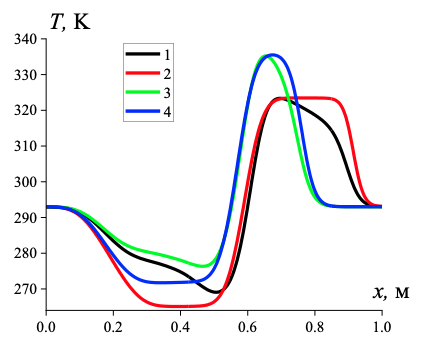
Рисунок 4 - Распределение температуры газа и несущей среды для различных граничных условий в трубе
Примечание: 1 − граничные условия Дирихле, однородный газ; 2 − граничные условия Неймана, однородный газ; 3 − граничные условия Дирихле, несущая среда газовзвеси; 4 − граничные условия Неймана, несущая среда газовзвеси
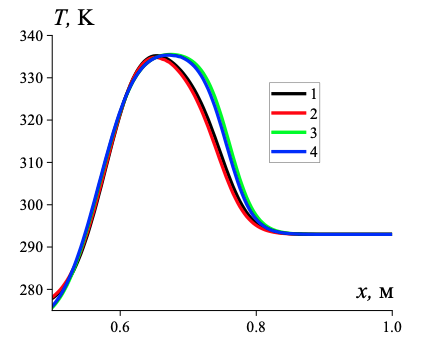
Рисунок 5 - Распределение температуры несущей среды газовзвеси и дисперсной фазы для различных граничных условий в трубе
Примечание: граничные условия Дирихле: 1 − несущая среда; 2 − дисперсная фаза, однородный газ; граничные условия Неймана: 3 − несущая среда; 4 − дисперсная фаза
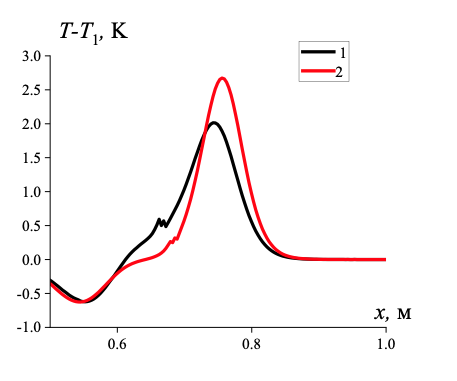
Рисунок 6 - Распределение разности температур несущей среды и дисперсной фазы
Примечание: 1 − граничные условия Дирихле; 2 − граничные условия Неймана
При задании граничных условий Неймана скорость распространения возмущения выше, разность температур несущей и дисперсной фазы отличается в большей степени, чем при граничных условий Дирихле — рисунок 6.
При моделировании распространения ударной волны с граничными условиями Неймана в однородном газе наблюдается большая скорость распространения ударной волны, чем при моделировании течения с граничными условиями Дирихле.
4. Заключение
В статье рассмотрены ударноволновые течения однородного газа и газовзвеси в канале. Математическая модель течения однородного газа и газовзвеси учитывала вязкость газа. При этом математическая модель позволяла учесть воздействие дисперсной фазы на течение газа. Целью работы было определить влияние выбора граничных условий на процесс моделирования работы ударно-волновой трубы. Выявлено, что для однородных граничных условий Дирихле, которые в большей степени соответствуют процессу движения ударной волны в канале, наблюдается меньшая скорость распространения ударной волны, а также меньшая величина параметров «температурного скольжения» фаз неоднородной среды. Результаты могут быть применены при моделировании ударноволновых течений газовзвесей в каналах и трубах.
