ДЕЦЕНТРАЛИЗОВАННОЕ УПРАВЛЕНИЕ ХАРАКТЕРИСТИЧЕСКИМИ ПОКАЗАТЕЛЯМИ ЛЯПУНОВА ВЗАИМОДЕЙСТВУЮЩИХ ХИМИЧЕСКИХ РЕАКТОРОВ

Технологическим процессам в химической промышленности, включая и процессы в системах химических реакторов, присущ ряд специфических свойств: многомерность (высокая размерность вектора состояния); много связность (наличие взаимодействия между подсистемами); нелинейный характер динамики и неконтролируемые параметрические возмущения

При исследовании процессов, протекающих в химических реакторах, и синтезе управляющих воздействий широкое распространение получили методы на основе пространства состояний, использующих описание динамики в виде многомерных систем дифференциальных уравнений в форме Коши

При управлении химическими реакторами исторически первыми были пропорционально-интегрально-дифференцирующие (ПИД) регуляторы

Цель исследования состоит в уменьшении затрат на вычисление параметров регулятора и увеличение устойчивости (робастности) системы взаимосвязанных химических реакторов. Для уменьшения затрат на синтез и реализацию регулятора, по сравнению с централизованной структурой управления

В качестве исходной принимается модель процессов в химическом реакторе, построенная при следующих допущениях: все реагенты образуют однофазную систему; поступающие элементы реагирующей смеси мгновенно перемешиваются с содержимым реактора и состояние смеси (концентрация, температура реагентов) в каждый момент времени будет иметь одинаковые значения во всём объеме реактора; теплоотвод от реакторов осуществляется через рубашку и все реакторы неизотермические (теплоотвод через стенку реактора осуществляется не мгновенно); реакторы проточного типа. В системе осуществляется экзотермическая реакция первого порядка, скорость реакции повышается с ростом температуры и подчиняется закону Аррениуса.

Структурная схема взаимодействующих химических реакторов. Схема взаимосвязей химических реакторов имеет следующий вид (см.рис. 1).

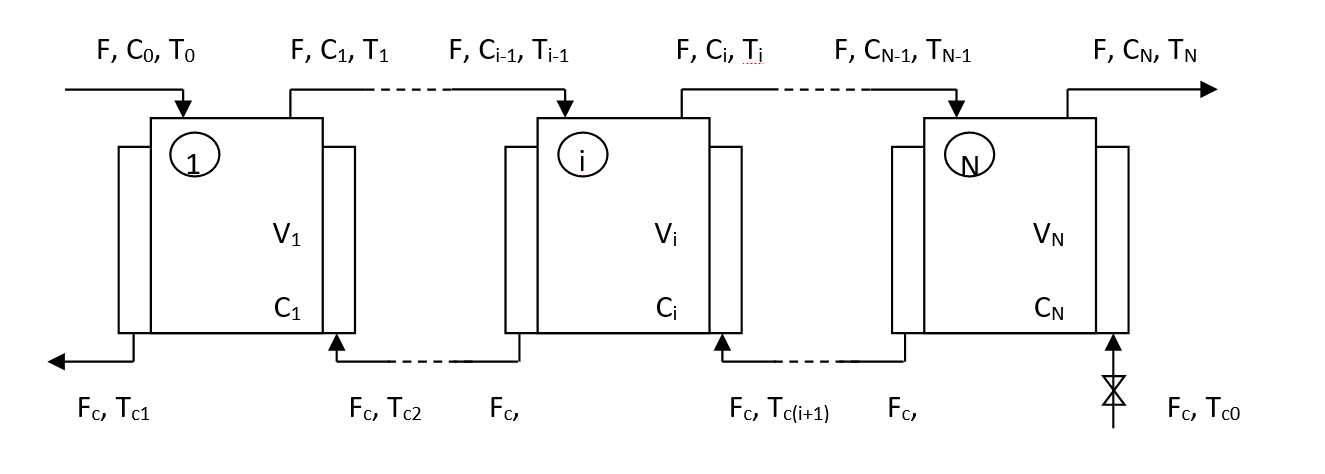
Рисунок 1 - Структурная схема взаимодействия химических реакторов

DOI:10.60797/IRJ.2024.147.11.1

На структурной схеме Fi – объемная скорость подачи вещества в i-й реактор; Ci-1, Ci – начальная и конечная концентрация вещества в i-м реакторе; Ti-1, Ti – температура на входе и выходе i-ого реактора; FC – объемная скорость подачи хладоагента в реакторы; TCi –температура хладагента в i-м реакторе.

Модель одиночного реактора. При принятых допущениях из закона сохранения массы следует дифференциальное уравнение, определяющее скорость изменения концентрации реагента в i-м реакторе

(1)

где Vi – рабочий объём i-ого реактора; K – множитель в законе Аррениуса; Ei – энергия активации реакции в i-м реакторе; R – универсальная газовая константа; здесь и далее  – производная по времени.

Из закона сохранения энергии получаем дифференциальное уравнение, определяющее скорость изменения температуры в i -м реакторе

(2)

где ΔHi – тепловой эффект реакции; ρi – удельная массовая теплоемкость реагента; γi – плотность реагента; Li – коэффициент теплопередачи; Si – площадь поверхности теплообмена.

Аналогично, для скорости изменения температуры хладагента в i-м реакторе справедливо

(3)

где ρС – удельная массовая теплоемкость хладоагента; γC – плотность хладоагента.

Если ввести вектор состояний

и вектор-функцию

,

где

(4)

тогда уравнения (1)-(4), описывающие динамику i-го реактора, можно представить в векторной форме

(5)

Модель системы взаимосвязанных реакторов. Для химических реакторов, соединенных последовательно, существует взаимное влияние реакторов друг на друга. По основному реагенту (i-1) -й реактор воздействует на i-й реактор, а по хладоагенту (i+1) реактор влияет на i-й. Векторная функция hi(z):Rn→Rn_i, определяющая степень влияния на i-й реактор (i-1)-го и (i+1)-го реакторов равна

(6)

Здесь

(7)

(8)

а z=(z1,z2,...,zN)T∈Rn – вектор состояний. Уравнения (5)-(8) определяют переходный процесс в i-м реакторе с учётом взаимодействия в форме системы нелинейных дифференциальных уравнений в нормальной форме Коши

(9)

Модель системы, состоящей из цепочки N последовательно соединенных реакторов, путем объединения уравнений (9), может быть представлена в векторной форме

(10)

где – вектор-функция, описывающая динамические свойства исследуемой системы химических реакторов.

Одна из особенностей нелинейных систем, включая и химические реакторы, состоит в возможности возникновения процессов, характеризующихся неустойчивостью особых точек, которые определяют режимы оборудования, вплоть до появления хаотической динамики.

Количественной мерой этой неустойчивости являются характеристический показатель Ляпунова, который вводится следующим образом. Характеристическим показателем функции z(t) называется число (или символ ±∞), определенное как

Среди всего набора характеристических показателей Ляпунова наиболее важен наибольший (старший) показатель χ1=χmax. Набор характеристических показателей, упорядоченных по убыванию χ1≥χ2≥ ...≥χn, определяет спектр Ляпунова нелинейной динамической системы.

Пусть нелинейная система химических реакторов совместно с управляющим воздействием описываются автономным векторным дифференциальным уравнением

(11)

где z(t)∈Rn – вектор состояния; u(t)∈Rm – вектор управления, m≤n; F(z(t))=(fi(z(t)))ni=1 – векторная функция, удовлетворяющая условиям существования решений уравнения (11); fi(z(t)) – вещественные функции, определенные и непрерывные по совокупности аргументов.

Задача стабилизации (увеличение степени устойчивости) состояния равновесия (рабочего режима системы химических реакторов) заключается в преобразовании сигнатуры спектра Ляпунова вида

в сигнатуру вида

(12)

или иными словами – смещение спектра вида (12) в открытой левой полуплоскости на расстояние α>0 от мнимой оси. В данном случае коэффициент α определяет степень устойчивости нелинейной системы.

Для решения этой задачи будем искать управление в виде обратной связи по вектору состояния нелинейной системы (11)

(13)

которое обеспечит в замкнутой системе спектр характеристических показателей Ляпунова

с сигнатурой вида (12).

Для уменьшения вычислительных затрат на синтез управление нелинейной системой (11) необходимо реализовать с учетом структурных ограничений в виде регулятора (13) с децентрализованной структурой

(14)

Децентрализованный регулятор – совокупность локальных регуляторов (14), реализующих обратную связь по фазовому вектору подсистем (11).

Спектр характеристических показателей Ляпунова нелинейной системы зависит от собственных значений матрицы Якоби линеаризованной системы. Изменение собственных чисел матрицы Якоби влечёт за собой изменение характеристических показателей Ляпунова нелинейной системы. Задать желаемые собственные числа матрице Якоби можно с помощью методики синтеза модального управления на основе решения линейных матричных неравенств.

Правомочность такого подхода обосновывается теоремами о структурной устойчивости (грубости) нелинейных динамических систем и топологической эквивалентности нелинейной системы и гиперболической линеаризованной модели

Линеаризация нелинейной системы. Пусть уравнение (11) описывает отклонения фазовых координат нелинейной системы взаимосвязанных химических реакторов от некоторой особой точки, в которой она удерживается с помощью управляющего воздействия. Используя формулу Тейлора в предположении дифференцируемости компонент функции F(z(t))=(fi (z(t)))ni=1 в окрестности особой точки, преобразуем уравнение (11) к квазилинейному виду

(15)

В уравнении (15) A(z*) – матрица Якоби нелинейной системы (11), равна

(16)

Если для отклонений значений фазовых координат нелинейной системы от номинальных значений

выполняются оценки

а матрица Якоби (16) не имеет собственных чисел на мнимой оси, тогда для синтеза управления, стабилизирующего нелинейную систему (11), в силу теоремы Гробмана-Хартмана, может быть использовано линеаризованное уравнение

(17)

Синтез централизованного регулятора. С помощью методики синтеза на основе линейных матричных неравенств

В соответствии с вторым методом Ляпунова система (17) будет асимптотически устойчивой если у неё существует положительно определённая функция Ляпунова

с ,

производная которой в силу системы (17) является отрицательно определённой функцией

(18)

С учётом (17) неравенство (18) имеет вид

(19)

умножая которое слева и справа на матрицу P-1 и обозначая G=P-1, имеем

(20)

Таким образом, синтез стабилизирующего управления сводится к вычислению пары матриц (G, K), удовлетворяющих матричным неравенствам (20). Введём новую матричную переменную L=KG и запишем неравенства (20) в виде

(21)

Параметры искомой обратной связи вычисляются по формуле

(22)

где матрицы L и G решения матричных неравенств (21).

Система (17) будет иметь степень устойчивости α, если область корней характеристического уравнения замкнутой системы на комплексной плоскости ограничивается областью, расположенной строго левее вертикальной линии, которая отстоит от мнимой оси на расстоянии -α. Это требование будет выполнено если полная производная квадратичной функции Ляпунова удовлетворяет условию

из которого следует необходимость выполнения условия

(23)

Параметры обратной связи также вычисляются по формуле (22).

Синтез децентрализованного управления. Для построения децентрализованного управления и уменьшения вычислительных затрат при проектировании матрица Р в неравенстве (19) должна иметь диагональную структуру. Выполним тождественное преобразование неравенства (19), приводящее к диагональной структуре его решения. В силу представления матриц A в виде суммы двух матриц – блочной диагональной AD и блочной недиагональной AO, равенства B=BD и выполнения структурного ограничения K=KD, неравенство (19) преобразуется к двум неравенствам следующего вида

(24)

(25)

умножая неравенство (24) слева и справа на матрицу P-1 и обозначая G=P-1, имеем

(26)

Неравенство (25) накладывает ограничения на интенсивность взаимного влияния подсистем.

Так как матрицы AD, BD, KD имеют блочную диагональную структуру, то матрица G также будет иметь аналогичную структуру и неравенство (26) эквивалентно N «расщепленным» неравенствам меньшей размерности, которые соответствуют изолированным подсистемам,

(27)

Таким образом, синтез стабилизирующего управления сводится к вычислению пары матриц (Gii, Kii), удовлетворяющих матричным неравенствам (27). Введя новую матричную переменную Lii=KiiGii, запишем неравенства (27) в виде

(28)

Стабилизирующее управление принимает искомую децентрализованную структуру

(29)

Из условия обеспечения степени устойчивости α_ii, следует необходимость выполнения условия

(30)

И стабилизирующее управление вычисляется по формуле (28).

В особой точке нелинейной системы взаимосвязанных химических реакторов (10)

при постоянных параметрах Vi=0,08см3, K=2000с-1, Ei=42290Дж/моль, ρi=4190000Дж/кгК, R=8,314Дж/моль, ΔHi=-146538Дж/моль, Si=0,09м2, γi=0,001кг/м3, Li=167,472Дж/м2с, ρC=4190Дж/кгК, γC=0,001кг/см3, F=0,0025 м3/с, Fc=0,002 м3/с и начальных условиях Ci(0)=6 моль/м3, Ti(0)=302 К, Tci(0)=298 К матрица Якоби (16) имеет вид

Спектр характеристических показателей Ляпунова равен

Близость старшего характеристического показателя Ляпунова к мнимой оси свидетельствует о возможности потери устойчивости при незначительных изменениях параметров системы. Степень устойчивости может быть увеличена сдвигом спектра Ляпунова влево путем введения управляющего воздействия в виде обратной связи по вектору состояния.

Централизованное управление. Задавшись степенью устойчивости α=-5 и решая линейные матричные неравенства (23), находим матрицы

и по формуле (22) коэффициент обратной связи

Для системы химических реакторов (11), замкнутой централизованным регулятором с найденным коэффициентом обратной связи, спектр Ляпунова смещается влево. Последнее свидетельствует об увеличении степени устойчивости замкнутой системы на заданную величину.

Децентрализованное управление. Матрицы Якоби, соответствующие изолированным реакторам (5), имеют вид

, ,

Задавшись степенью устойчивости αi=-5 для каждого химического реактора и решая линейные матричные неравенства (30), находим матрицы

и по формуле (29) коэффициент обратной связи децентрализованного регулятора

Для системы химических реакторов (11), замкнутой децентрализованным регулятором с найденным коэффициентом обратной связи, спектр Ляпунова равен

Значения характеристических показателей Ляпунова свидетельствует: о регулярной динамике химических реакторов; об увеличении степени устойчивости замкнутой синтезированным управлением системы на заданную величину; об уменьшении времени переходного процесса в системе.

На рис. 2, для примера, представлены временные диаграммы переходных процессов по концентрации реагента в первом реакторе без управляющего воздействия, с централизованным и децентрализованным управлением. Графики 2б и 2в иллюстрируют уменьшение длительности переходного процесса по концентрации реагента в одном из трех химических реакторов при централизованном и децентрализованном управлении. Затухание переходного процесса свидетельствует об устойчивости по Ляпунову исследуемой системы. Сравнение централизованного и децентрализованного управления по длительности переходного процесса для всех трех компонент фазового вектор и трех химических реакторов приведено в табл. 1. Величины, приведенные в табл. 1 и полученные на основе расчетов по значениям характеристических показателей, говорят об уменьшении длительности переходных процессов при децентрализованном управлении примерно в 100 раз.

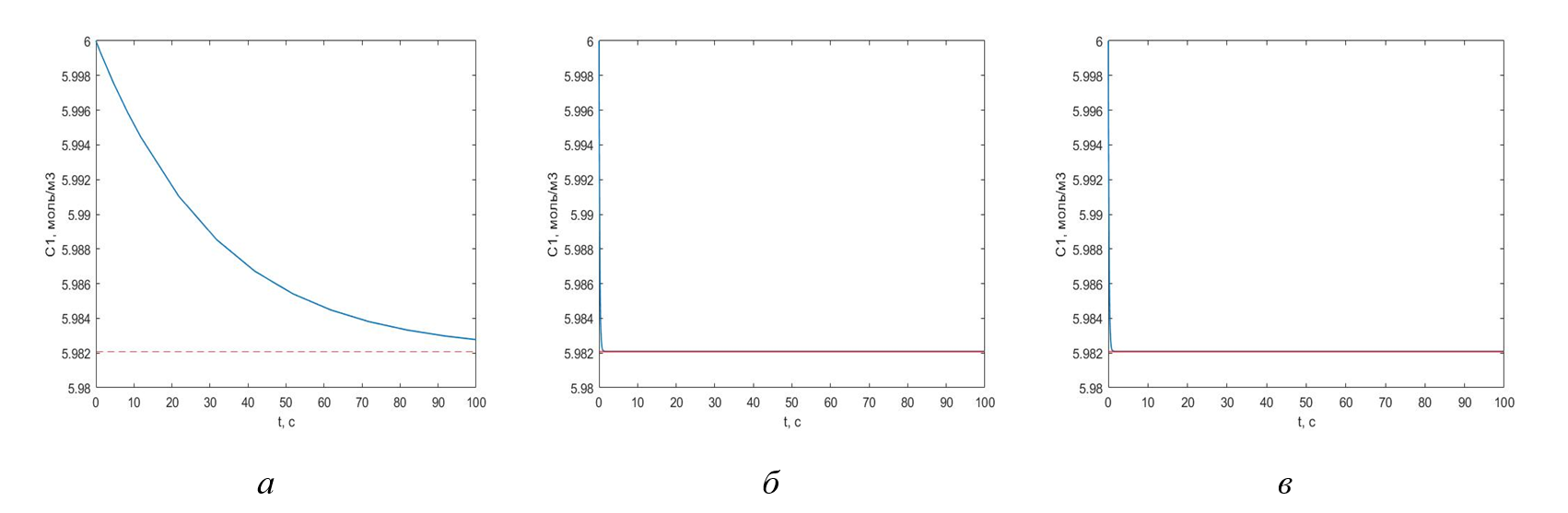
Рисунок 2 - Переходные процессы по концентрации реагента в первом реакторе:

а - без управления; б - с централизованным управлением; в - с децентрализованным управлением

DOI:10.60797/IRJ.2024.147.11.2

где:

Ci – концентрация вещества в i -м реакторе, моль/м2

Ti – температура на выходе i -ого реактора, К

TC_i – температура хладагента в i -м реакторе, К.

Цель работы, состоящая в уменьшении затрат на синтез и увеличение робастности по отношению к параметрическим возмущениям, достигнута, что подтверждается выполненными аналитическими расчетами и математическим моделированием взаимодействующих химических реакторов с синтезированным децентрализованного управлением. Синтез децентрализованного регулятора осуществлен на основе декомпозиции исходного линейного матричного неравенства размерности n на систему неравенств меньшей размерности ni (n> ni). Увеличение устойчивости, и как следствие робастности, замкнутой системы достигнуто смещением спектра характеристических показателей Ляпунова влево по вещественной оси путем введения обратной связи, параметры которой рассчитаны методом модального управления, обобщенного на нелинейный случай.