Наши журналы
Опубликовать статью Вход и регистрация
Расширенный поиск
Разделы статьи

ВЕЙВЛЕТ АНАЛИЗ МНОГОЛЕТНЕГО СМЕЩЕНИЯ СЕВЕРНОГО ПОЛЮСА ЗЕМЛИ

Научная статья
Курбасова Г.С.
Рыхлова Л.В.
DOI:
https://doi.org/10.23670/IRJ.2021.9.111.021
Выпуск: № 9 (111), 2021
Опубликована:
2021/09/17
PDF

ВЕЙВЛЕТ АНАЛИЗ МНОГОЛЕТНЕГО СМЕЩЕНИЯ СЕВЕРНОГО ПОЛЮСА ЗЕМЛИ

Научная статья

Курбасова Г.С.1, *, Рыхлова Л.В.2

1 Крымская астрофизическая обсерватория РАН, Крым, Россия;

2 Институт астрономии РАН, Москва, Россия

* Корреспондирующий автор (gskurb[at]gmail.com)

Аннотация

В настоящей работе используются данные EOP (IERS) C 01 — это серия параметров ориентации Земли, заданных с интервалом 0,1 год за период (1846 - 1889) и 0,05 года на интервале с 1890 года по настоящее время. В условиях недостаточной наблюдательной информации в прошлом, анализ долговременных серий координат полюса основан на широком использовании модельных представлений о реальном его смещении, учитывающих свойственные вращению Земли внутренние связи.

Целью настоящей работы является анализ неоднородных серий координат полюса EOP (IERS) C 01 с помощью сравнительно нового математического аппарата вейвлетов. Этим методом для данных за период с 1846 по настоящее время получены пространственно-временная спектральная структура и долговременный тренд.

Разложив временные ряды на частотно-временное пространство, нами определены как доминирующие колебания с периодами 85.5 ± 0.5, 56 ± 0.5, 33 и 21год, так и то, как эти колебания меняются во времени.

Ключевые слова: полюс, системы координат, вейвлет, масштаб, долговременный тренд.

WAVELET ANALYSIS OF THE LONG-TERM DISPLACEMENT OF THE EARTH'S NORTH POLE

Research article

Kurbasova G.S.1, *, Rykhlova L.V.2

1 Crimean Astrophysical Observatory, Crimea, Russia;

2 Institute of Astronomy of the Russian Academy of Sciences, Moscow, Russia

* Corresponding author (gskurb[at]gmail.com)

Abstract

The current article uses the EOP (IERS) C 01, which is a series of Earth orientation parameters set at an interval of 0.1 years for the period from 1846 to 1889 and 0.05 years for the interval from 1890 to the present. In the conditions of insufficient observational data in the past, the analysis of long-term series of pole coordinates is based on the extensive use of model representations of its real displacement, taking into account the internal connections inherent in the rotation of the Earth.

The purpose of this study is to analyze the inhomogeneous series of coordinates of EOP (IERS) C 01 using a relatively new mathematical apparatus of wavelets. Using this method, a spatiotemporal spectral structure and a long-term trend are obtained for the data for the period from 1846 to the present.

Decomposing the time series into the time-frequency space, the article determines both the dominant fluctuations with periods of 85.5 ± 0.5, 56 ± 0.5, 33 and 21 years, and how these fluctuations change over time.

Keywords: pole, coordinate systems, wavelet, scale, long-term trend.

Развитие методов измерений, уточнение моделей природных процессов на основе высокоточных наблюдений изменили концепции системы Земля.

В прошлом наблюдения за вращением Земли относительно звезд проводились астрономическими методами на соответствующем астрономическом оборудовании. В настоящее время, вместо использования вращения Земли и движения Луны/планет для определения и реализации времени, в частности Всемирного Времени (Universal Time, UT), можно изучать вращение Земли и движение планет как функцию атомного времени или Универсального скоординированного времени (Coordinated Universal Time, UTC), которое сегодня получено однозначно из атомного времени. Этот аспект имеет особое значение для проблем, связанных с изучением и мониторингом вращения Земли.

В современной науке о Космосе существует большое число проблем связанных с пониманием явлений, с под­тверждением различных гипотез о структуре и эволюции небесных тел, их объединении в скопления или связанных с реальными фи­зическими законами во Вселенной. В основе изучения этих проблем лежат реальные наблюдения. При этом достоверность информации о наблюдаемых небесных объектах зависит от точности определения координат в соответствующей системе отсчёта.

Для материализации надежной и доступной системы отсчета необходимо построить систему координат, которая должна реализовываться во времени на высокоточной информации о параметрах ориентации Земли (ПОЗ). Знание параметров вращения Земли даёт нам основу для определения координат точек на земной поверхности: положение оси вращения Земли определяет систему широт и долгот. Кроме того, период вращения Земли даёт естественную единицу и естественный стандарт времени.

Параметры ориентации Земли постоянно изменяются. Так, ось вращения Земли не сохраняет своего положения ни в пространстве, ни по отношению к телу Земли. Первое явление, объясняемое прецессией и нутацией земной оси, известно давно и в настоящее время хорошо изучено [1], [2], [3]. Колебание полюсов, смещающих положение оси вращения относительно самой Земли, не смотря на большое практическое значение, изучено недостаточно. Вследствие колебания полюсов широты всех точек земной поверхности периодически изменяются на несколько сотых долей секунды дуги, что в линейной мере соответствует двум-трём десяткам метров. Кроме того, в настоящее время в ряде работ обсуждается возможность векового движении полюса [4], что могло бы повлиять на распределение климатических зон Земли. Ещё более серьёзные последствия вызывает недостаточно изученная неравномерность вращения Земли, которая проявляется в вековом замедлении вращения (сутки увеличиваются, примерно, на 0,015 сек в столетие). Наблюдаются небольшие сезонные изменения скорости вращения Земли: максимальные в августе, медленные в марте и доходящие до 0.034 сек. неправильные скачкообразные изменения [5].

Движение Северного полюса Земли

В первые годы деятельности Международной службы широты (МСШ) движение полюса определялось по непрерывным рядам наблюдений широты на станциях Мицузава (Япония), Китаб (Узбекистан), Карлофорте (Италия), Юкайя и Гейтерсберг (США), расположенных на «международной» параллели 39 с. Международным условным началом (МУН). Реальное положение МУН задавалось назначением широт станций МСШ.

Международная служба вращения Земли (The International Earth Rotation and Reference Systems Service, IERS) [6] была основана в 1987 году Международным астрономическим союзом и Международным союзом геодезии и геофизики. Она начала функционировать с 1 января 1988 года и заменила Международную службу по движению полюса (IPMS) и секцию вращения Земли Бюро Международного времени (BIH); деятельность BIH в настоящее время продолжается в Бюро Международного времени (International des Poids et Mesures, BIPM) [7], [8].

В основные задачи IERS входит обслуживание астрономических, геодезических и геофизических сообществ.

Более полные сведения о долговременных и периодических изменениях положения Северного полюса можно получить из публикаций в разделе анализа наблюдений IERS [6].

Непредсказуемые воздействия экзогенных и эндогенных факторов на кинематику и динамику Земли создают необходимость постоянной поддержки модели движения её полюса с помощью наблюдений. Поскольку неравномерности вращения Земли вызваны движением гидросферы и атмосферы, ни одна детерминированная модель не может описать их с точностью, сопоставимой с точностью наблюдений. Вращение Земли постоянно контролируется наблюдениями космической геодезии.

Анализ спектральной структуры данных о долговременном смещении Северного полюса по поверхности Земли, выявление физической информации о закономерностях этого движения необходимы для установления точной системы отсчёта, долговременных закономерных геофизических и солнечных связей в системе Земля.

Исходные данные

Центр ориентации Земли, расположенный в Парижской обсерватории, публикует в настоящее время два основных временных ряда координат смещения полюса по поверхности Земли: долгосрочное решение (IERSC01) с 1846 года до конца предыдущего года и бюллетень B / C04, выпускаемый с однодневными интервалами, который публикуется ежемесячно с 30-дневной задержкой [13].

В настоящей работе используются данные EOP (IERS) C 01 — это серия параметров ориентации земли, заданных с интервалом 0,1 год за период (1846 - 1889) и 0,05 года на интервале с 1890 года по настоящее время. Эта серия является основой системы долгосрочных исследований IERS, обновляемой регулярно один раз в месяц. Комбинированный временной ряд основан на следующих данных:•1846 - 1899: решение, полученное Л.В. Рихловой из трех серий программ абсолютного склонения в Пулково, Гринвиче, Вашингтоне [14].• 1900-1961: Решение Вондрака и др. (1995), полученное с помощью серий оптической астрометрии [15]. • 1962 – по настоящее время: в результате следующих астрометрических измерений:• 1993 - н.в.: космическая техника VLBI, LLR, SLR и GNSS.• 1989 - 1992: космическая техника VLBI, LLR, SLR• 1962 - 1979: оптическая астрометрия (решения BIH); космическая техника, начиная с 1969 года (LLR, UT) и с 1972 г. – Доплер, движение полюса.В настоящее время проведено полное обновление данных по CO1 за период 1900–1906 гг. Обновлённые координаты полюса лучше согласуются с данными условного международного начала (CIO). Прежняя версия представляла ложный сдвиг в интервале 1900-1962 гг. [16]. Более подробную информацию об этапах решения проблемы стыковки различных серий данных в долговременных временных рядах параметров смещения Северного полюса можно найти в публикациях IERS [6].

О методе вейвлет анализа

Долговременные серии координат движения полюса Земли получены из неравноточных серий наблюдений на конечных интервалах времени. Поэтому возникает задача достоверности пространственно временного представления этих данных.

В последние десятилетия современные методы спектрального анализа дополняет вейвлет анализ. Вейвлет обработка цифровых сигналов и изображений сформировались в целое научное направление [17], [18], [19], [20]. Идеи теории вейвлетов возникли, когда появилось достаточное количество рядов экспериментальных данных, обработка которых стандартным и хорошо развитым методом преобразования Фурье показала его ограниченность для поиска закономерностей в них [21]. Метод вейвлет преобразования применяется в настоящее время для анализа локализованных изменений мощности во временном ряду. Разложив временной ряд на частотно-временное пространство, можно определить как доминирующие режимы изменчивости, так и то, как эти режимы меняются во времени.

«Вейвлет преобразование одномерного сигнала состоит в его разложении по базису, сконструированному из обладающей определёнными свойствами функции (вейвлета) посредством масштабных изменений и переносов. Каждая из функций этого базиса характеризует как определённую (временную) частоту, так и её локализацию в физическом пространстве» [17, С. 1145].

Существует два подхода к анализу нестационарных временных рядов, какими являются анализируемые в настоящей работе серии данных. Первый, оконное преобразование Фурье (Windowed Fourier transform, WFT), основан на локальном преобразовании Фурье (short-time Fourier transform) [20], [22].

Оконное преобразование Фурье представляет собой неточный и неэффективный метод частотно-временной локализации. Неточность возникает из-за наложения спектров высокочастотных и низкочастотных компонентов, которые не попадают в частотный диапазон окна. Неэффективность возникает из-за частот, которые необходимо анализировать на каждом временном шаге, независимо от размера окна или присутствующих доминирующих частот.

Второй подход заключается в использовании вейвлет преобразования. Вейвлеты непосредственно связаны с многомасштабным анализом и обработкой сигналов различной природы. Вейвлет анализ при каждом масштабе позволяет увидеть те особенности сигнала, которые характерны для данного масштаба, эффективно отфильтровывая влияние других масштабов.

Вейвлет преобразование можно использовать для анализа временных рядов, содержащих нестационарную мощность на многих разных частотах. Предположим, что имеется временной ряд 03-10-2021 11-34-18 с одинаковым интервалом отсчёта времени 03-10-2021 11-34-28. Предположим также, что имеется волновая функция 03-10-2021 11-34-36, которая зависит от безразмерного параметра времени η. Чтобы быть «допустимой» в качестве вейвлета, эта функция должна иметь нулевое среднее значение и быть локализованной как во временном, так и в частотном пространстве [17], [23]. Примером может служить вейвлет Морле, состоящий из плоской волны, модулированной гауссианом [23]:

03-10-2021 11-35-06    (1) где 03-10-2021 11-35-27 - безразмерная частота, принимаемая здесь равной 6, чтобы удовлетворять условию допустимости.

Непрерывное вейвлет преобразование дискретной последовательности x определяется как свертка x с масштабированной и транслированной версией 03-10-2021 11-36-16:

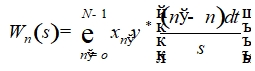03-10-2021 11-36-24     (2) где символ * обозначает комплексное сопряжение. Изменяя масштаб вейвлета s и перемещая по локализованному временному индексу n можно построить картину, показывающую как амплитуду любых характеристик в зависимости от масштаба, так и то, как эта амплитуда изменяется со временем. Чтобы аппроксимировать непрерывное вейвлет преобразование, свертка (2) должна выполняться N раз для каждого масштаба, где N - количество точек во временных рядах [24].

Выбирая N - точек, теорема о свертке позволяет нам выполнять все N сверток одновременно в пространстве Фурье, используя дискретное преобразование Фурье (ДПФ).

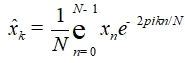03-10-2021 11-40-32    (3) где 03-10-2021 11-40-40 – индексы частоты. В непрерывном представлении преобразование Фурье функции 03-10-2021 11-40-48 дается выражением 03-10-2021 11-41-02.

По теореме о свертке вейвлет - преобразование является обратным преобразованием Фурье произведения:

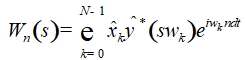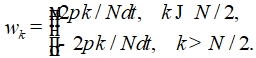03-10-2021 11-41-11    (4) где угловая частота определяется как 03-10-2021 11-41-24      (5) Используя (4) и стандартную процедуру преобразования Фурье, можно вычислить непрерывное вейвлет-преобразование (для данного s) для всех n одновременно и эффективно. Вейвлет преобразование можно использовать для анализа временных рядов, содержащих нестационарную мощность на многих разных частотах [25].

Вейвлет анализ серий координат среднего полюса Земли1. Непрерывное вейвлет преобразование серий данных xp и yp.

Непрерывное вейвлет преобразование используется в случае анализа локальной дифференцируемости функции, а также для обнаружения и характеристики ее возможных особенностей [23].

В непрерывном вейвлет преобразовании данных анализирующей функцией является вейвлет . При этом сжатая или растянутая версия вейвлета  сравнивается с последовательностью данных. Растяжение или сжатие функции в совокупности называется расширением или масштабированием и соответствует физическому понятию масштаба. Сравнивая последовательность серий дискретных данных с вейвлетом в различных масштабах a и параметра смещения b, мы получаем функцию двух переменных. Для параметра масштаба 03-10-2021 11-47-43 и параметра смещения b непрерывное вейвлет преобразование имеет вид

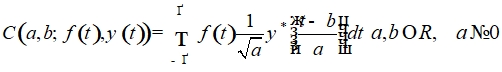03-10-2021 11-47-58    (6)

где 03-10-2021 11-48-05 – анализируемая функция, символ  ⃰ обозначает комплексное сопряжение. Коэффициенты вейвлет преобразования 03-10-2021 11-48-14 содержат комбинированную информацию об анализируемом сигнале и об используемом вейвлете. Изменяя масштаб вейвлета  и перемещая по локализованному временному индексу , можно построить картину, показывающую как амплитуду любых характеристик в зависимости от масштаба, так и то, как эта амплитуда изменяется со временем.

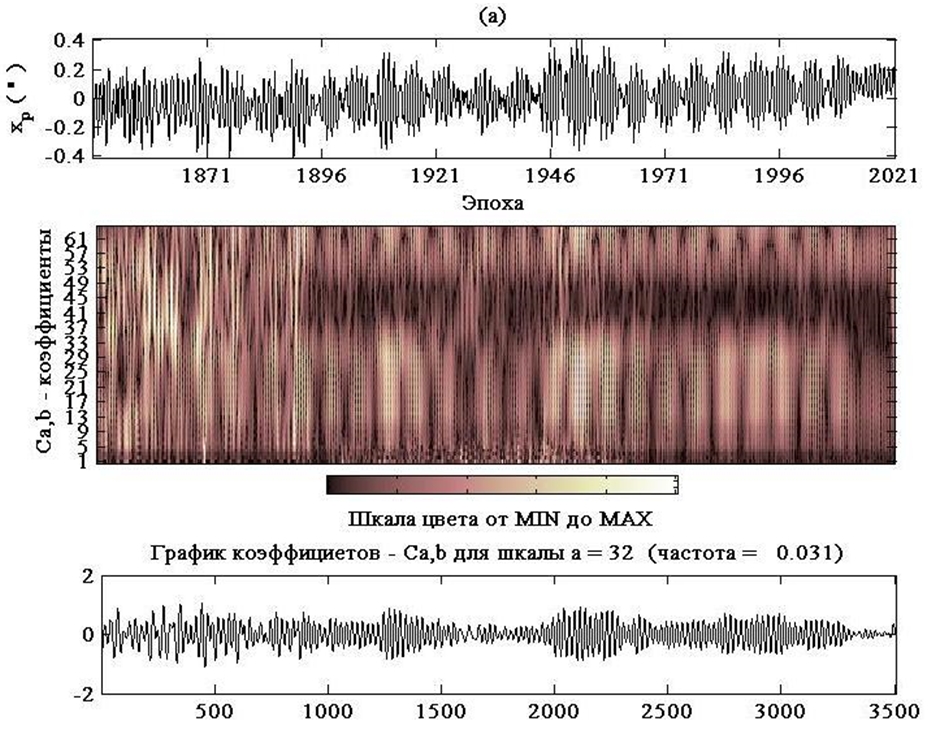
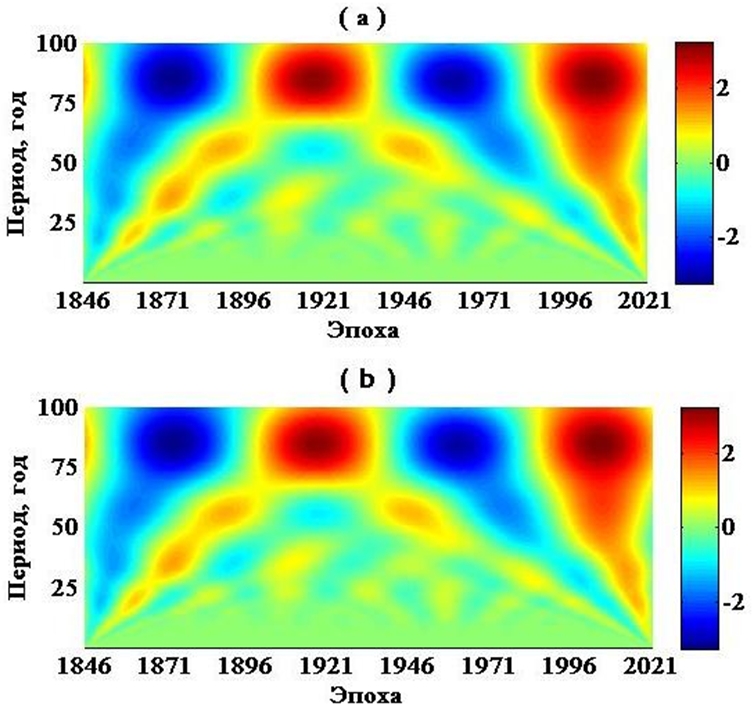
Непрерывное вейвлет преобразование серий координат  03-10-2021 11-48-25, заданных на интервале с 1846 по настоящее время демонстрирует рисунок 1.

03-10-2021 11-59-21

Рис. 1 – Непрерывное вейвлет преобразоание данных о координатах Северного полюса Земли за период с 1846 года по настоящее время (EOP C 01, IERS):а – координаты 03-10-2021 11-52-47 в угловых секундах, коэффициенты 03-10-2021 11-52-56 для шкалы масштабов a от 1 до 61 , график коэффициентов 03-10-2021 11-52-56 для шкалы 03-10-2021 11-53-24 соответствующий частоте 0.031 (1/ масштаб); b – координаты  03-10-2021 11-53-46 в угловых секундах, коэффициенты 03-10-2021 11-52-56 для шкалы масштабов a от 1 до 61 , график коэффициентов  03-10-2021 11-52-56 для шкалы 03-10-2021 11-53-24  соответствующий частоте 0,031 (1/ масштаб)Примечание: большим величинам  шкалы масштабов соответствуют более низкие частоты и наоборот; для вейвлет преобразования использовались вейвлеты 'bior 2.2'

 

Информативность вейвлет преобразования данных зависит от свойств используемых вейвлетов. В работах Дебуши И. [25], [26] приведены характеристики основных «семейств» вейвлетов.

Картина на рисунке 1 получена нами путём вейвлет преобразования данных с использованием биортогональных сплайн-вейвлетов (сокращённое имя 'bior2.2'). Использование биортогональных вейвлетов представляет собой новый подход, первоначально предложенный в контексте прерывного вейвлет-преобразования. Сущность его состоит в замене вейвлета  на два вейвлета, один из которых используется для анализа, а другой – для реконструкции. В таком виде биортогональные вейвлеты очень перспективны, потому что они имеют гораздо большую гибкость в выборе вейвлета, чем ортогональные вейвлеты. Мы можем, например, выбрать свойства обоих вейвлетов как дополнительные, с сокращениями высокого порядка для анализирующего вейвлета и хорошей регулярностью для синтезирующего вейвлета [23].

Основные характеристики этих вейвлетов: биортогональные сплайн-вейвлеты, для которых возможны симметрия и точная реконструкция с FIR-фильтрами. В ортогональном случае это невозможно, кроме вейвлетов Хаара [26].Цветовой индикатор позволяет оценить изменение энергии колебаний в пространстве (времени) для различных масштабов (частот). На рисунке 1 выделяется диапазон масштабов, в котором уровень энергии колебаний сравнительно низкий после 1899 года, что, очевидно, связано с фильтрацией соответствующего диапазона частот.

2. Выделение нелинейных долговременных трендов

Bейвлет – преобразование является инструментом кратно масштабного анализа, который позволяет рассматривать исследуемый сигнал с различными масштабами. Такой анализ позволяет, с одной стороны, выделять кратковременные локальные особенности сигнала, незаметные на фоне его глобальных изменений. С другой стороны, можно «отфильтровать» высокочастотные изменения сигнала, сосредоточившись на изучении его глобальных, долговременных эволюций, что было использовано нами для выделения долговременного тренда.

С этой целью был проведен выбор подходящего семейства вейвлетов как эмпирически так и с учётом свойств вейвлетов, обеспечивающих наилучшую аппроксимацию долговременных изменений анализируемых временных рядов. В результате выбраны вейвлеты из семейства «DMeyer» ("Discrete" Meyer Wavelet), сокращённое название 'dmey’.

Перечислим основные свойства этих вейвлетов: обеспечивают ортогональный и биортогональный анализы, допускают непрерывное и дискретное вейвлет преобразования.

Соответствующая этим вейвлетам вейвлет функция представлена в виде [27]:

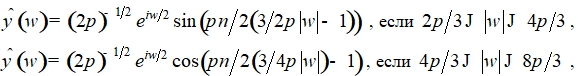03-10-2021 12-04-13   (7)

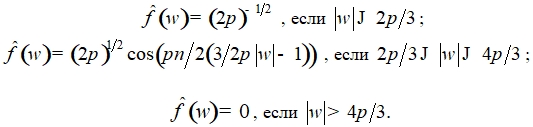где 03-10-2021 12-03-46 а функция шкалы представлена выражениями: 03-10-2021 12-04-33    (8)

В приведенных математических описаниях (2) и (3) a – масштаб, n – вспомогательная функция, изменяя которую получаем различные вейвлеты семейства.

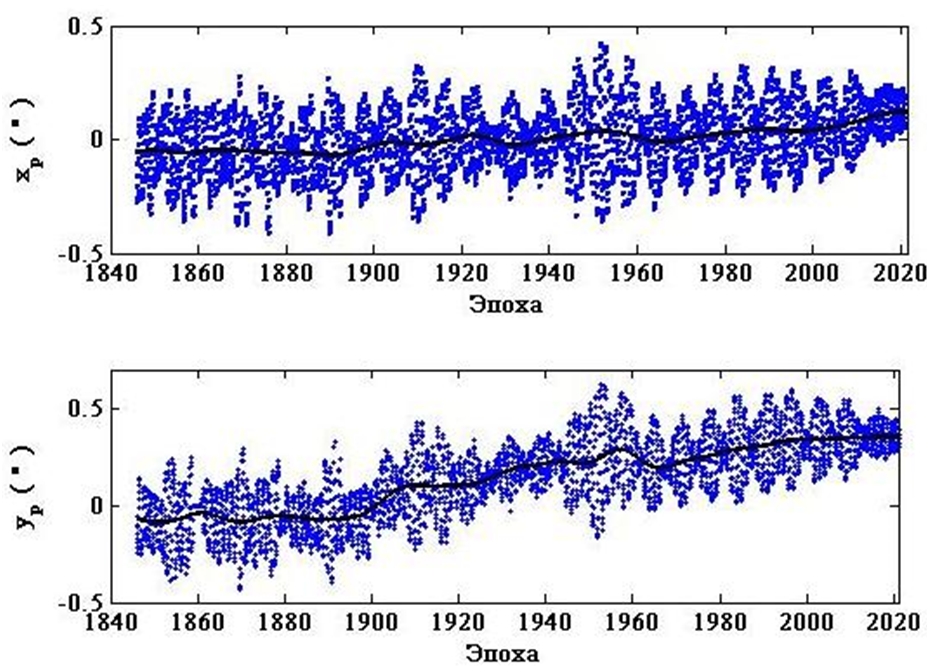
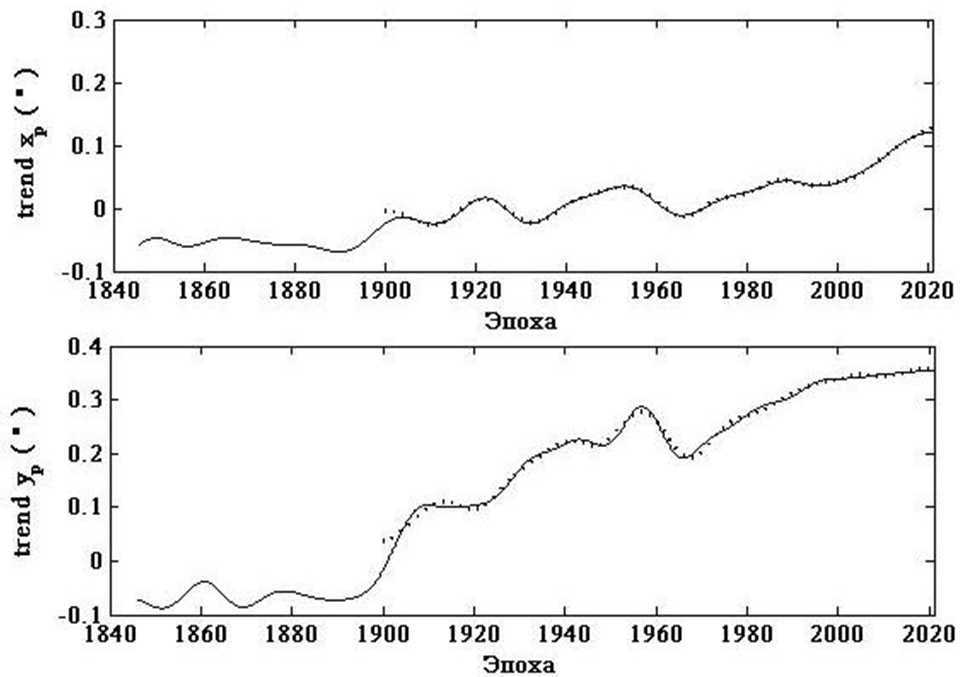
Процедура выделения нелинейных трендов в настоящей работе состояла в последовательном вейвлет преобразовании серий данных на различных уровнях детализации и статистической проверке результатов аппроксимации. Графики на рисунке 2 демонстрируют выделеные долговременные тренды.

На рисунке 3, приведены графики долговременных трендов в сериях данных на интервалах с 1846 года и с 1900 года по настоящее время. Сравнение графиков на рисунке 3 выявляет видимые расхождения на интервале порядка 2 лет с 1900 года.

03-10-2021 12-07-11

Рис. 2 – Нелинейные треды в данных 03-10-2021 11-48-25: серии данных с 1846 года по настоящее время (звёздочки), нелинейные тренды (непрерывные кривые)

03-10-2021 12-07-45

Рис. 3 – Графики нелинейных трендов выделенных в данных  03-10-2021 11-48-25 на различных интервалах времени: сплошная линия – на интервале с 1846 года; пунктирная – с 1900 года по настоящее время

 

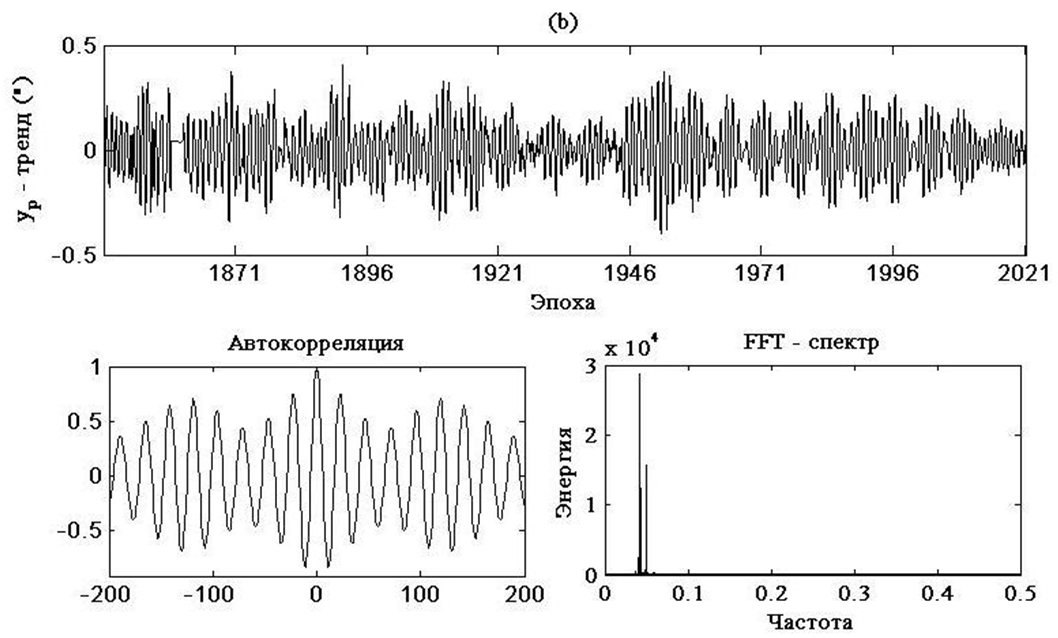
Выполним статистический анализ разностей между сериями данных 03-10-2021 11-48-25,  за период с 1846 года по настоящее время и долговременными нелинейными трендами (см. Рис. 2). Результаты статистического анализа приведены на рисунке 4 и в Таблице 1.

03-10-2021 12-09-58

Рис. 4 – Статистический анализ разностей после удаления из серий  03-10-2021 11-48-25 долговременных трендов

Графики автокорреляций и FFT – спектров на рисунке 4 обнаруживают в анализируемых разностях два наиболее мощных систематических колебания не принадлежащих к области выделенных нами низких частот. Дискретные статистики разностей в Таблице 1 демонстрируют значимость этих колебаний.

Таблица 1 – Дискретные статистики серий координат хр, yp после удаления трендов

Среднее Медиана Мода R Std
хр ('') -6,48х10-5 1,93х10-5 0,015 0,78 0,13
yp ('') 5,28х10-5 0,0017 0,043 0,80 0,13

Для анализа спектральной структуры долговременных трендов (см. Рис. 3) установим связь между преобразованием Фурье и вейвлет представлениями анализируемых временных рядов.

Взаимосвязь между частотой и длительностью

Прямого соответствия между длиной волны Фурье и масштабом нет. Однако мы можем найти коэффициенты преобразования для выбранных вейвлетов, которые дают приблизительное соответствие масштаб-частота (период).

Изменение масштаба a вейвлета приводит к пропорциональному изменению его центральной частоты:

03-10-2021 12-13-27    (9)

где 03-10-2021 12-13-47, – частота на масштабе a, 03-10-2021 12-13-54– центральная частота вейвлета на масштабе 1, Δ – период дискретизации. Таким образом, изменяя масштаб вейвлет преобразования, можно перекрыть весь частотный диапазон исследуемого сигнала. Кроме того, за счет хорошей временной локализации вейвлет преобразования можно получить информацию о спектре буквально в каждой точке сигнала. При анализе периодов колебаний в приведенных нами частотно-временных разложениях сигнала использовались вейвлеты Морле. 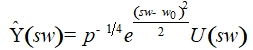Аналитический вейвлет Морле определяется в области Фурье следующим образом [28]: 03-10-2021 12-14-52     (10) где 03-10-2021 12-15-06 – функция Хевисайда. 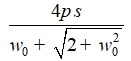Масштабный коэффициент Фурье для вейвлета Морле равен [28]:   03-10-2021 12-15-18   (11)

Спектральный состав долговременных трендов в сериях xp и yp

03-10-2021 12-21-12

Рис. 5 – Частотно временная локализация колебаний в долговременных трендах серий данных 03-10-2021 11-48-25

Установленная нами линейная связь между шкалой коэффициентов и периодами синусоидальных колебаний позволила определить величины основных трёх периодических колебаний в данных о долговременных трендах.

Самым мощным (см. шкалу цвета справа) оказалось колебание с периодом 85.5 ± 0.5 года. Следующее, достаточно регулярное на интервале с 1846 года по настоящее время, – с периодом 56.5 ± 0.5 года. Мощность третьего и четвёртого колебания с периодами 33 года и 21 год существенно убывает после 1900 года.

Выводы

В условиях недостаточной наблюдательной информации в прошлом, анализ долговременных серий координат полюса основан на широком использовании модельных представлений о реальном его смещении учитывающих свойственные вращению Земли внутренние связи. Модельные представления дополняют математические методы анализа.

С целью анализа серий координат среднего полюса Земли за период с 1846 года по настоящее время, нами предложен метод вейвлет анализа, позволяющий анализировать данные в пространственно-временном разложении (см. Рис. 1). Картина вейвлет разложения, приведенная на рисунке 1, демонстрирует неоднородность обработки наблюдений и ширину полосы масштабов (с1900 года), в которой величина энергии колебаний подавлена.

Так как длительность ряда существенно влияет на достоверность определения долговременного тренда, нами использовались серии данных с 1846 года по настоящее время.

В результате непрерывного частотно временного вейвлет анализа в спектральной структуре долговременного тренда установлены колебания с периодами 85.5, 56.5, 33 и 21 год.

Конфликт интересов Не указан. Conflict of Interest None declared.

 

Список литературы / References

  1. Жаров В. Е. Сферическая астрономия / В. Е. Жаров. — Фрязино, 2006. — 480 с. ISBN 5–85099–168–9
  2. Жаров В.Е. Теория нутации неупругой Земли / В.Е. Жаров, С.Л. Пасынок // Астрономический журнал. 2001, том 78, №11, стр.1034-1048.
  3. Молоденский М. С. Земные приливы и нутация Земли / М. С. Молоденский, М. В. Крамер. [Сб. ст.], М., 1961.
  4. Schuh, H. Linear drift and periodoc variations observed in long time series of polar motion / H. Schuh, S. Nagel, T. Seitz // Journal of Geodesy, 74; pp. 701-710.
  5. Манк У. Макдональд. Вращение Земли / Манк У. Макдональд. – М.: Мир, 1964. – 384 с.
  6. International Earth Rotation and Reference Systems Service (IERS), Earth Orientation Parameters, EOP (IERS) 08 C04. [Electronic resource] URL: https://datdcenter.iers.org./eop/. (accessed: 12.06.2021)
  7. CIPM, 1971, 59th session o f the Comitt International des Poids et Mesures, BIPM, Sevres.
  8. IERS, Ann. Reports, [Electronic resource] URL: http://www.iers.org/iers/publications/reports/ (accessed: 12.06.2021)
  9. Dickman, S.R. Investigation of controvertial polar motion features using homogeneous ILS data / S.R. Dickman // J. Geophys. Res. 86, pp.4904-4912.
  10. Gross, R.S. A determination an Analysis of polar motion / R.S. Gross. Ph.D. dissert.; University of Colorado. 1982.
  11. MacCarthy D. D. Path of the mean rotational pole from 1899 to 1994 / D. D. MacCarthy, B. J. Luzum // Geophys. J. International, 125, pp. 623-629.
  12. Wahr John M. Deformation induced by polar motion / M. Wahr John // Featured in Journal of Geophysical Research: Solid Earth. Volume 90, Issue B11. 30 September 1985 P. 9363–9368.
  13. Bizouard C. The IERS EOP 14C04 solution for Earth orientation parameters consistent with ITRF 2014 / C. Bizouard, S. Lambert, C. Gattano et al. // J. of Geodesy, doi:10.1007/s00190-018-1186-3
  14. Рыхлова Л.В. Движение полюса Земли в 1846.0 - 1891.5 по наблюдениям в Пулково, Гринвиче и Вашингтоне / Л.В. Рыхлова // А.Ж., Т. 45 № 5, 1968 г. С. 1132 -1133.
  15. Vondrak J. Earth orientation parameters based on EOP-C4 Astrometric catalog / J. Vondrak, C. Ron, V. Stefka // Acta Geodyn. Geomat.
  16. IERS Annual reports EOP (IERS) C 01.
  17. Астафьева Н.М. Вейвлет анализ: основы теории и примеры применения / Н.М. Астафьева // УФН. 1998. Т.166. Вып.11. С.1145-1170
  18. Бурнаев Е.В. Применение вейвлет преобразования для анализа сигналов: Учебно-методическое пособие / Е.В. Бурнаев. – М.: МФТИ, 2007. – 138 с.
  19. Вейвлеты в астрономии. [Электронный ресурс] URL: https://clck.ru/XDYt3 (дата обращения: 12.06.2021)
  20. Добеши И. Десять лекций по вейвлетам / И. Добеши. М.: НИЦ “Регулярная и хаотическая динамика”, 2004, 464 с.
  21. Марпл-мл. С.Л. Цифровой спектральный анализ и его приложения / С.Л. Марпл-мл.: Пер. с англ. -М.: Мир, 1990. .–584 с.
  22. Duhamel P. "Fast Fourier Transforms: A Tutorial Review and a State of the Art / P. Duhamel, M. Vetterli // Signal Processing, Vol. 19, April 1990, pp. 259-299.
  23. Farge M. Wavelet transforms and their applications to turbulence / M. Farge // Annu. Rev. Fluid Mech., 24, 395-457.
  24. Kaiser G. A Friendly Guide to Wavelets / G. Kaiser. Birkhauser, 300 pp.
  25. Daubechies, I. The wavelet transform time-frequency localization and signal analysis / I. Daubechies // IEEE Trans. Inform. Theory, 36, 961-1004.
  26. Daubechies I. Ten Lectures on Wavelets / I. Daubechies // Society for Industrial and Applied Mathematics, 357 pp.
  27. Abry P. Ondelettes et turbulence / P. Abry: Diderot ed., Paris, 1997, p. 268.
  28. Torrence, C. A Practical Guide to Wavelet Analysis. / C. Torrence, G.P. Compo // Bulletin of the American Meteorological Society Vol. 79, No. 1, 61-78.

Список литературы на английском языке / References in English

  1. Zharov V. E. Sfericheskaja astronomija [Spherical astronomy] / V. E. Zharov. - Fryazino, 2006. - 480 p. ISBN 5-85099-168-9 [in Russian]
  2. Zharov V. E. Teorija nutacii neuprugoj Zemli [Theory of nutation of the inelastic Earth] / V. E. Zharov, S. L. Pasynok // Astronomicheskij zhurnal [Astronomical Journal]. 2001, volume 78, No. 11, pp. 1034-1048. [in Russian]
  3. Molodensky M. S. Zemnye prilivy i nutacija Zemli [Earth tides and nutation of the Earth] / M. S. Molodensky, M. V. Kramer. [Collection of articles], M., 1961. [in Russian]
  4. Schuh, H. Linear drift and periodoc variations observed in long time series of polar motion / H. Schuh, S. Nagel, T. Seitz // Journal of Geodesy, 74; pp. 701-710.
  5. Monk W. McDonald. Vrashhenie Zemli [The rotation of the Earth] / Monk W. McDonald. - Moscow: Mir, 1964 – - 384 p. [in Russian]
  6. International Earth Rotation and Reference Systems Service (IERS), Earth Orientation Parameters, EOP (IERS) 08 C04. [Electronic resource] URL: https://datdcenter.iers.org./eop/. (accessed: 12.06.2021)
  7. CIPM, 1971, 59th session o f the Comitt International des Poids et Mesures, BIPM, Sevres.
  8. IERS, Ann. Reports, [Electronic resource] URL: http://www.iers.org/iers/publications/reports/ (accessed: 12.06.2021)
  9. Dickman, S.R. Investigation of controvertial polar motion features using homogeneous ILS data / S.R. Dickman // J. Geophys. Res. 86, pp.4904-4912.
  10. Gross, R.S. A determination an Analysis of polar motion / R.S. Gross. Ph.D. dissert.; University of Colorado. 1982.
  11. MacCarthy D. D. Path of the mean rotational pole from 1899 to 1994 / D. D. MacCarthy, B. J. Luzum // Geophys. J. International, 125, pp. 623-629.
  12. Wahr John M. Deformation induced by polar motion / M. Wahr John // Featured in Journal of Geophysical Research: Solid Earth. Volume 90, Issue B11. 30 September 1985 P. 9363–9368.
  13. Bizouard C. The IERS EOP 14C04 solution for Earth orientation parameters consistent with ITRF 2014 / C. Bizouard, S. Lambert, C. Gattano et al. // J. of Geodesy, doi:10.1007/s00190-018-1186-3
  14. Rykhlova L. V. Dvizhenie poljusa Zemli v 1846.0 - 1891.5 po nabljudenijam v Pulkovo, Grinviche i Vashingtone [The movement of the Earth's pole in 1846.0-1891.5 according to observations in Pulkovo, Greenwich and Washington] / L. V. Rykhlova // A. Zh., Vol. 45 No. 5, 1968, pp. 1132 -1133.
  15. Vondrak J. Earth orientation parameters based on EOP-C4 Astrometric catalog / J. Vondrak, C. Ron, V. Stefka // Acta Geodyn. Geomat.
  16. IERS Annual reports EOP (IERS) C 01.
  17. Astaf'eva N. M. Vejvlet analiz: osnovy teorii i primery primenenija [Wavelet analysis: basic theory and applications] / N. M. Astafieva // UFN. 1998. Vol. 166. Issue.11. P. 1145-1170
  18. Burnaev E. V. Primenenie vejvlet preobrazovanija dlja analiza signalov [Application of wavelet transform for signal analysis]: textbook / E. V. Burnaev. – M.: MFTI, 2007. – 138 p.
  19. Vejvlety v astronomii [Wavelets in astronomy]. [Electronic resource] URL: https://clck.ru/XDYt3 (accessed: 12.06.2021)
  20. Dobeshi I. Desjat' lekcij po vejvletam [Ten lectures on wavelets] / I. Dobeshi. M.: SIC "Regular and chaotic dynamics", 2004, 464 p.
  21. Marple-ml. S. L. Cifrovoj spektral'nyj analiz i ego prilozhenija [Digital spectral analysis and its applications] / S. L. Marple-ml.: Trans. from English-M.: Mir, 1990. .-584 p.
  22. Duhamel P. "Fast Fourier Transforms: A Tutorial Review and a State of the Art / P. Duhamel, M. Vetterli // Signal Processing, Vol. 19, April 1990, pp. 259-299.
  23. Farge M. Wavelet transforms and their applications to turbulence / M. Farge // Annu. Rev. Fluid Mech., 24, 395-457.
  24. Kaiser G. A Friendly Guide to Wavelets / G. Kaiser. Birkhauser, 300 pp.
  25. Daubechies, I. The wavelet transform time-frequency localization and signal analysis / I. Daubechies // IEEE Trans. Inform. Theory, 36, 961-1004.
  26. Daubechies I. Ten Lectures on Wavelets / I. Daubechies // Society for Industrial and Applied Mathematics, 357 pp.
  27. Abry P. Ondelettes et turbulence / P. Abry: Diderot ed., Paris, 1997, p. 268.
  28. Torrence, C. A Practical Guide to Wavelet Analysis. / C. Torrence, G.P. Compo // Bulletin of the American Meteorological Society Vol. 79, No. 1, 61-78.