АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ НА ОСНОВЕ ПОКОМПОНЕНТНОГО СОПОСТАВЛЕНИЯ ЗНАКОВ РЕШЕНИЯ, ПЕРВОЙ И ВТОРОЙ ПРОИЗВОДНОЙ РЕШЕНИЯ

АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ  НА ОСНОВЕ ПОКОМПОНЕНТНОГО СОПОСТАВЛЕНИЯ ЗНАКОВ РЕШЕНИЯ,  ПЕРВОЙ И ВТОРОЙ ПРОИЗВОДНОЙ РЕШЕНИЯ

Научная статья

Буланов С.Г.*

ORCID: 0000-0002-8532-4172,

Таганрогский институт имени А.П. Чехова (филиал) РГЭУ (РИНХ), Таганрог, Россия

* Корреспондирующий автор (bulanovtgpi[at]mail.ru)

Аннотация

Предложен подход к анализу устойчивости в смысле Ляпунова систем линейных обыкновенных дифференциальных уравнений. Подход основан на покомпонентном сопоставлении знаков решения, первой и второй производной решения. Установлены комбинации знаков, которые являются достаточными условиями устойчивости, асимптотической устойчивости и неустойчивости. Отличительной особенностью предложенного подхода является то, что не используются методы качественной теории. Теоретические положения доведены до практической программной реализации. Приближенные значения решения, первой и второй производной решения находятся на основе разностных методов. Проведен программный и численный эксперимент в условиях меняющихся систем линейных обыкновенных дифференциальных уравнений, длины промежутка решения, разностных методов решения.

Ключевые слова: устойчивость по Ляпунову, компьютерный анализ устойчивости, численное моделирование устойчивости.

AN ANALYSIS OF THE STABILITY OF SYSTEMS OF LINEAR DIFFERENTIAL EQUATIONS BASED ON A COMPONENT-BY-COMPONENT COMPARISON OF THE SIGNS OF THE SOLUTION, THE FIRST AND SECOND DERIVATIVES OF THE SOLUTION

Research article

Bulanov S.G.*

ORCID: 0000-0002-8532-4172,

A.P. Chekhov Taganrog Institute (branch) of Rostov State University of Economics, Taganrog, Russia

* Corresponding author (bulanovtgpi[at]mail.ru)

Abstract

The current article proposes an approach to the analysis of stability in the sense of Lyapunov systems of linear ordinary differential equations. The approach is based on a component-by-component comparison of the signs of the solution, the first and second derivatives of the solution. Combinations of signs that are sufficient conditions for stability, asymptotic stability and instability are established. A distinctive feature of the proposed approach is that the methods of qualitative theory are not used. The theoretical provisions have been brought towards practical program implementation. Approximate values of the solution, the first and second derivatives of the solution are found on the basis of difference methods. A program and numerical experiment are carried out under the conditions of changing systems of linear ordinary differential equations, the length of the solution interval, and difference methods of solution.

Keywords: Lyapunov stability, computer analysis of stability, numerical modeling of stability.

Введение

Методы анализа устойчивости в смысле Ляпунова систем линейных обыкновенных дифференциальных уравнений (ОДУ) находят применение в различных областях науки и техники [1], [2]. Вместе с тем отмечается недостаток внедрения компьютерных технологий в области анализа устойчивости, включая задачи устойчивости систем линейных ОДУ с переменной матрицей коэффициентов. Такое внедрение представляется важным для приложений и теории, поскольку к системам линейных ОДУ с помощью линеаризации сводится анализ устойчивости некоторых общих методов качественной теории дифференциальных уравнений и методов, основанных на векторно-матричных мультипликативных и аддитивных преобразованиях разностных схем численного интегрирования [3], [4]. Прикладная значимость разработки компьютерного анализа устойчивости особо актуальна для исследования устойчивости систем линейных ОДУ при моделировании работы генераторов в энергетических системах большой мощности [5].

Рассмотрим задачу Коши для системы линейных ОДУ вида

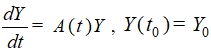     (1)

Ниже используется норма вектора  понимается значение k-й компоненты решения, первой и второй производной решения в точке .

Предполагается, что , такое, что для (1) выполнены все условия существования и единственности решения ,  на  и для каждого его возмущения с начальным вектором, удовлетворяющим условию . Элементы матрицы , размерности , определены, непрерывны и непрерывно дифференцируемы.

Ставится задача разработать подход к анализу устойчивости системы (1) в смысле Ляпунова. Подход строится в предположении, что ограниченность компонентов  может определяться знаком компонентов  – знаком компонентов . Покомпонентное сопоставление знаков решения, первой и второй производной решения приводит к достаточным условиям устойчивости, асимптотической устойчивости и неустойчивости системы (1).

Методы и принципы исследования

Всюду ниже на устойчивость исследуется нулевое решение системы (1). Величина возмущения нулевого решения обозначается . Формулируемые ниже утверждения следуют из представленных в [6] для нелинейных автономных систем с учетом свойств систем линейных ОДУ:

1. Если 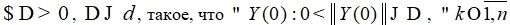, верны неравенства 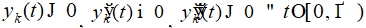, то решение системы (1) устойчиво.

В данных условиях функция  не возрастает, поэтому . Следовательно для .

2. Если 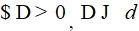 такое, что 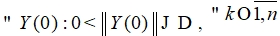, верны неравенства 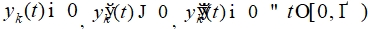, то решение системы (1) устойчиво.

Утверждение доказывается по аналогии с п.1.

3. Если для некоторых 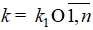 выполнены условия п.1, а для всех остальных  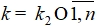– условия п.2, то решение системы (1) устойчиво.

Теорема 1. Если решение задачи (1) устойчиво и  ,  выполняется пара неравенств , и при этом , то решение системы (1) асимптотически устойчиво.

Доказательство. Для  произвольно зафиксируем  и выберем , при котором выполняется . Предположение, что , окажется в противоречии с устойчивостью. При этом предположении, , такое что, начиная с некоторого , выполняется неравенство:

Тогда 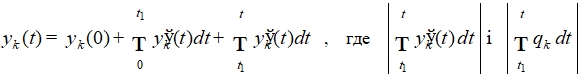, 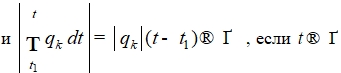. Отсюда.

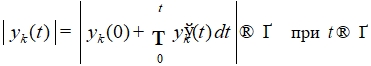Последнее свидетельствует о неустойчивость нулевого решения, что противоречит условию. Предположение неверно, поэтому в рассматриваемых условиях выполняется . Поскольку , с учетом произвольности выбора , соотношение . Поэтому решение системы асимптотически устойчиво. Аналогично выполняется доказательство для случая .

Теорема 2. Пусть решение системы (1) устойчиво. Если , выполняется пара неравенств , то решение системы (1) асимптотически устойчиво.

Доказательство. Пусть зафиксировано . При выполнении первой пары неравенств функция  убывает и ограничена снизу. Поэтому . Если предположить, что , возникнет противоречие.

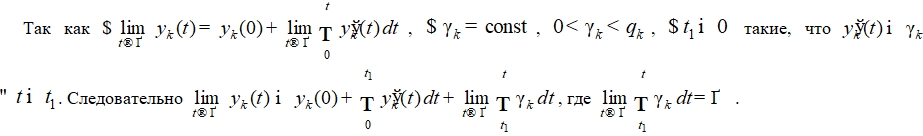
Поэтому  вопреки устойчивости. Предположение неверно, следовательно . С учетом произвольности выбора  возможно только, если . Отсюда следует асимптотическая устойчивость решения системы (1). Аналогично выполняется доказательство для случая .

Теорема 3. Если для задачи (1)  такие, что выполняется пара неравенств , при этом выполняется , то решение системы (1) неустойчиво.

Доказательство. Пусть для определенности выполняются неравенства . Если функция . При этом  с учетом возрастания . Если в этом случае предположить, что решение устойчиво и , то необходимо . Следовательно , что противоречит . Если предположить, что решение устойчиво и , то функция  ограничена, не убывает, следовательно, имеет предел , что противоречит устойчивости. Остается предположить, что  не ограничено сверху, но это также означает, что решение неустойчиво. Случай ,  доказывается аналогично.

Численный и программный эксперимент

Эксперимент проводился с помощью ПК на базе процессора Intel(R) Core(TM) i5-4460 в среде программирования Delphi. Написаны программы, на основе которых находятся приближенные значения решения системы (1), первой и второй производной решения. Требуемые приближения ниже находятся на основе метода Рунге-Кутта. Системы исследуются при значении шага разностной схемы , величина возмущения начальных данных , промежуток решения . Использование метода Батчера 6-го и Дормана-Принса 8-го порядков требует больших временных затрат при неизменной трактовке характера устойчивости исследуемых систем.

Пример 1. Исследуется на устойчивость система [7]

   (2)

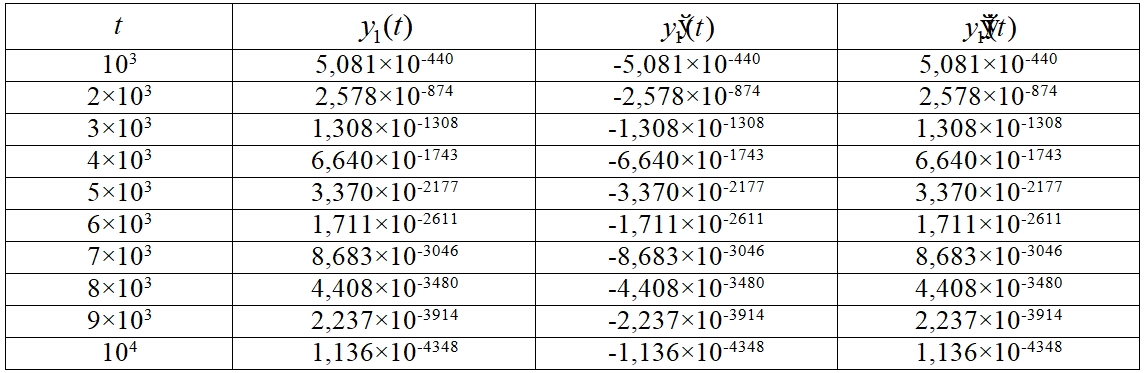
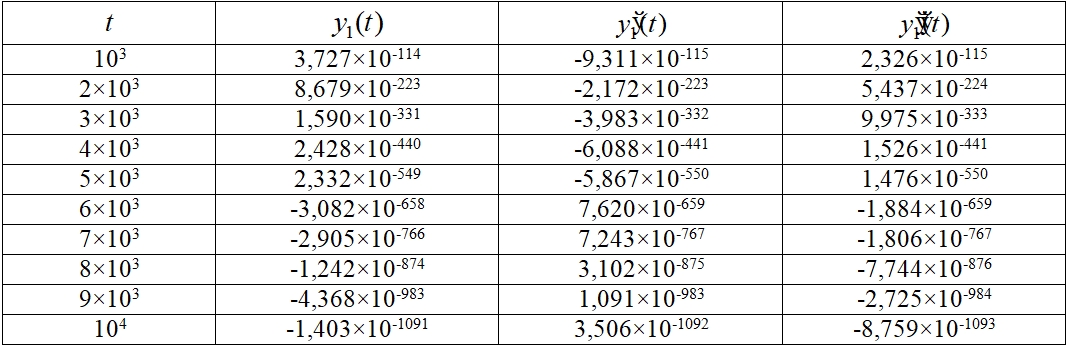
В [7] выполнялся анализ устойчивости системы (2) на основе матричных мультипликативных критериев и было установлено, что система асимптотически устойчива. В табл. 1 и табл. 2 приводятся численные значения решения, первой и второй производной решения системы (1) в десяти узловых точках.

 

Таблица 1 – Численные значения  системы (2)

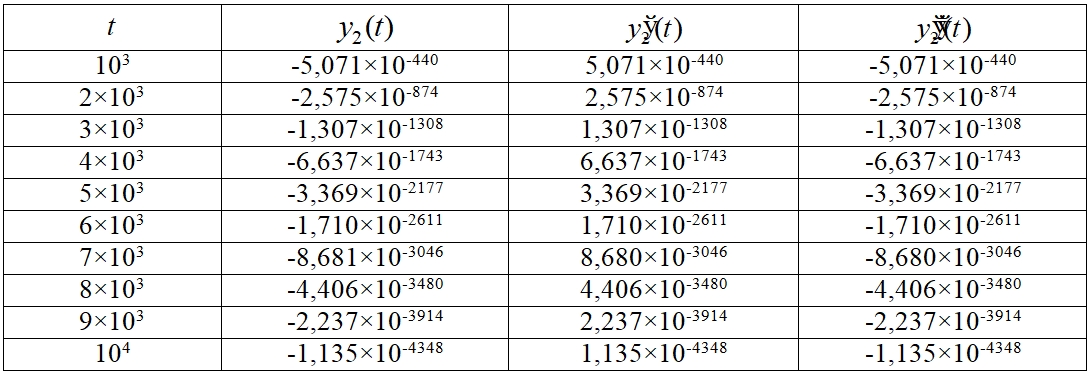
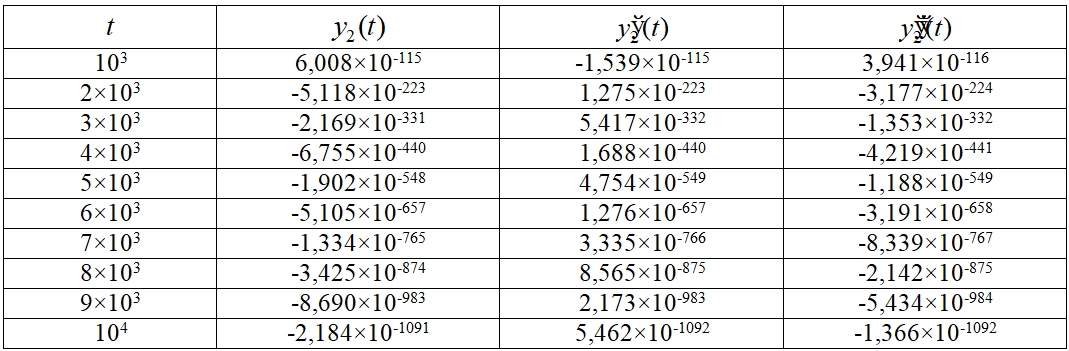
Таблица 2 – Численные значения  системы (2)

В целом программа позволяет находить отрезки, на которых сохраняется определенная комбинация знаков решения, первой и второй производной решения. На основе численного эксперимента было установлено, что комбинация знаков  сохраняется при , а комбинация . В соответствии с теоремой 1 и теоремой 2 это свидетельствует об асимптотической устойчивости системы (2).

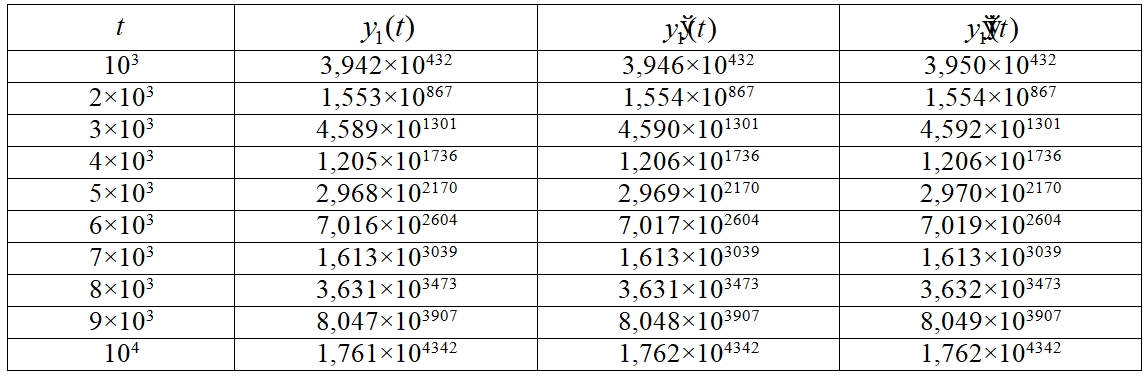
Пример 2. Исследуется на устойчивость система

    (3)  

Таблица 3 – Численные значения  системы (3)

Для первой компоненты решения, первой и второй производной решения на всем промежутке выполняется комбинация знаков .

 

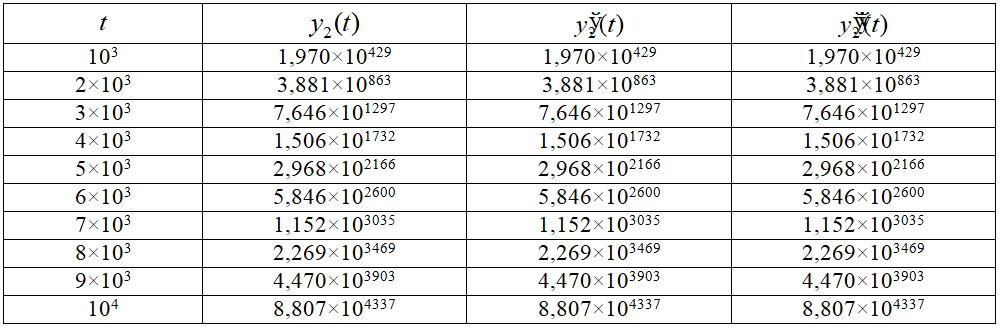
Таблица 4 – Численные значения  системы (3)

Аналогичный результат имеет место для второй компоненты. В соответствии с теоремой 3 это свидетельствует о неустойчивости системы (3).

Пример 3. Исследуется на устойчивость нулевое решение нелинейной системы

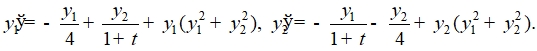    (4)

В табл. 5 и табл. 6 представлены численные значения решения, первой и второй производной решения системы (4). Согласно представленным выше условиям, полученные комбинации знаков свидетельствуют об асимптотической устойчивости нулевого решения системы (4). При этом в отличие от предыдущих случаев для первой компоненты решения и ее производных наблюдается переход от комбинации знаков  к комбинации . Аналогичный результат имеет место для второй компоненты решения и ее первой и второй производной.

 

Таблица 5 – Численные значения  системы (4)

Таблица 6 – Численные значения   системы (4)

Так как нелинейные добавки , стремятся к нулю при стремлении к нулю  то анализ устойчивости системы (4), согласно теореме Ляпунова об устойчивости по первому приближению, может быть сведен к анализу линеаризованной системы

   (5)

При анализе устойчивости системы (5) комбинации знаков решения, первой и второй производной решения для обоих компонент получились тождественными представленным в табл. 5, 6. Численные значения решения, первой и второй производной решения линеаризованной системы, с точностью не менее трех знаков после запятой совпадают с соответствующими им значениями нелинейной системы (4). Таким образом, результаты анализа устойчивости нелинейной системы и линеаризованной системы оказались в полном соответствии и свидетельствуют об асимптотической устойчивости нулевого решения системы (4).

Предложенный подход наряду с методом на основе матричных мультипликативных критериев [8], [9] может служить основой для разработки компьютерной технологии анализа устойчивости. Для нахождения приближенного значения решения систем линейных ОДУ с более высокой степенью точности, чем на основе разностных методов целесообразно применять метод варьируемого кусочно-интерполяционного приближения [10]. В результате помимо достигаемой точности решения, сокращается время на исследование, как следствие появляется возможность определять асимптотические свойства решения.

Заключение

Предложен подход к анализу устойчивости систем линейных ОДУ на основе покомпонентного сопоставления знаков решения, первой и второй производной решения. Отличительной особенностью подхода является, в частности, то, что при анализе устойчивости не требуется информация о характеристических числах и характеристических показателях. Подход доведен до компьютерной реализации. По результатам программного и численного эксперимента в режиме реального времени делается однозначный вывод о характере устойчивости исследуемых систем линейных ОДУ.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Giesl P. Computation of Lyapunov functions for nonlinear discrete time systems by linear programming / P. Giesl, S. Hafstein // J. Difference Equ. Appl. – 2014. – V. 20. – I. 4. – P. 610–640.
2. Zhaolu T. A numerical algorithm for Lyapunov equations / Zhaolu, G. Chuanqing // J. Appl. Math. Comput. – 2008. – V. 202. – I. 1. – P. 44–53.
3. Bulanov S.G. Differential systems stability analysis based on matrix multiplicative criteria / S.G. Bulanov // Journal of Physics: Conference Series. – Applied Mathematics, Computational Science and Mechanics: Current Problems. – 2020. – 012103.
4. Bulanov S.G. Computer analysis of differential systems stability based on linearization and matrix multiplicative criteria / S.G. Bulanov // Journal of Physics: Conference Series. – Applied Mathematics, Computational Science and Mechanics: Current Problems. – 2021. – P. 012101.
5. РоммЯ.Е. Компьютерный анализ устойчивости систем линейных дифференциальных уравнений с приложением к оценке устойчивости синхронного генератора / Я.Е.Ромм, С.Г. Буланов // Известия ЮФУ. Технические науки. – 2009. – №5 (94). – С. 52–59.
6. РоммЯ.Е. Компьютерно-ориентированный анализ устойчивости решений дифференциальных систем / Я.Е.Ромм // Современные наукоемкие технологии. – 2020. – № 4. – С. 42–63.
7. РоммЯ.Е. Метод компьютерного анализа устойчивости систем линейных дифференциальных уравнений / Я.Е.Ромм, С.Г. Буланов // Деп. в ВИНИТИ. – 30.04.2009. – №  – 119 с.
8. РоммЯ.Е. Численный эксперимент по компьютерному анализу устойчивости линеаризованных систем нелинейных дифференциальных уравнений / Я.Е.Ромм, С.Г. Буланов // Деп. в ВИНИТИ. – 14.07.2016. – №  – 18 с.
9. РоммЯ.Е. Численный эксперимент по компьютерному анализу устойчивости решений обыкновенных дифференциальных уравнений на основе критериев матричного вида / Я.Е.Ромм, С.Г. Буланов // Деп. в ВИНИТИ. – 14.08.2017. – № 89. – 20 с.
10. БулановС.Г. Программный анализ устойчивости систем обыкновенных дифференциальных уравнений на основе мультипликативных преобразований разностных схем и кусочно-полиномиальных приближений решения / С.Г.Буланов, Г.А. Джанунц // Промышленные АСУ и контроллеры. – 2015. – № 2. – С. 10–20.

Список литературы на английском языке / References in English

1. Giesl P. Computation of Lyapunov functions for nonlinear discrete time systems by linear programming / P. Giesl, S. Hafstein // J. Difference Equ. Appl. – 2014. – V. 20. – I. 4. – P. 610–640.
2. Zhaolu T. A numerical algorithm for Lyapunov equations / Zhaolu, G. Chuanqing // J. Appl. Math. Comput. – 2008. – V. 202. – I. 1. – P. 44–53.
3. Bulanov S.G. Differential systems stability analysis based on matrix multiplicative criteria / S.G. Bulanov // Journal of Physics: Conference Series. – Applied Mathematics, Computational Science and Mechanics: Current Problems. – 2020. – 012103.
4. Bulanov S.G. Computer analysis of differential systems stability based on linearization and matrix multiplicative criteria / S.G. Bulanov // Journal of Physics: Conference Series. – Applied Mathematics, Computational Science and Mechanics: Current Problems. – 2021. – P. 012101.
5. Romm Ya.E. Komp'juternyj analiz ustojchivosti sistem linejnyh differencial'nyh uravnenij s prilozheniem k ocenke ustojchivosti sinhronnogo generatora / Ya.E. Romm, S.G. Bulanov [The computer analysis of a stability of systems of linear differential equations with application to an estimation stabilities of the synchronous generator] // Izvestija JuFU. Tehnicheskie nauki [Izvestiya SFedU. Engineering sciences] – 2009. – №5 (94). – P. 52–59. [in Russian]
6. Romm Ya.E. Komp'juterno-orientirovannyj analiz ustojchivosti reshenij differencial'nyh sistem [Computer-oriented stability analysis of solutions of differential systems] / Ya.E. Romm // Sovremennye naukoemkie tehnologii [Modern high technologies]. – 2020. – № 4. – P. 42–63. [in Russian]
7. Romm Ya.E. Metod komp'juternogo analiza ustojchivosti sistem linejnyh differencial'nyh uravnenij [Method of computer analysis of stability of systems of linear differential equations] / Ya.E. Romm, S.G. Bulanov // Dep. v VINITI [Dep. in VINITI]. – 30.04.2009. – № 268. – 119 p. [in Russian]
8. Romm Ya.E. Chislennyj jeksperiment po komp'juternomu analizu ustojchivosti linearizovannyh sistem nelinejnyh differencial'nyh uravnenij [Numerical experiment on computer analysis of stability of linearized systems of nonlinear differential equations] / Ya.E. Romm, S.G. Bulanov // Dep. v VINITI [Dep. in VINITI]. – 14.07.2016. – № 102. – 18 p. [in Russian]
9. Romm Ya.E. Chislennyj jeksperiment po komp'juternomu analizu ustojchivosti reshenij obyknovennyh differencial'nyh uravnenij na osnove kriteriev matrichnogo vida [Numerical experiment on computer analysis of solutions stability of ordinary differential equations based on criteria of matrix form] / Ya.E. Romm, S.G. Bulanov // Dep. v VINITI [ in VINITI]. – 14.08.2017. – № 89. – 20 p. [in Russian]
10. Bulanov S.G. Programmnyj analiz ustojchivosti sistem obyknovennyh differencial'nyh uravnenij na osnove mul'tiplikativnyh preobrazovanij raznostnyh shem i kusochno-polinomial'nyh priblizhenij reshenija [Program analysis of stability of ordinary differential equations systems on the basis of multiplicative transformations of difference schemes and piecewise polynomial approximations of the solution] / S.G. Bulanov, G.A. Dzhanunts // Promyshlennye ASU i kontrollery [Industrial Automatic Control Systems and Controllers]. – 2015. – № 2. – P. 10–20. [in Russian]