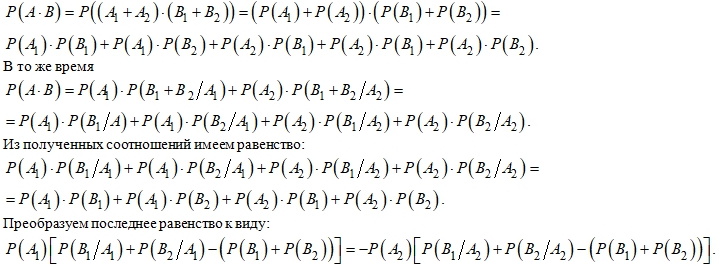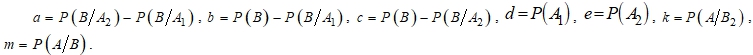CТОХАСТИЧЕСКАЯ НЕЗАВИСИМОСТЬ СЛОЖНЫХ СОБЫТИЙ

CТОХАСТИЧЕСКАЯ НЕЗАВИСИМОСТЬ СЛОЖНЫХ СОБЫТИЙ

Обзорная статья

Ганичева А.В.¹, Ганичев А.В.^2, *

¹ ORCID: 0000-0002-0224-8945;

² ORCID: 0000-0003-3389-7582;

¹ Тверская государственная сельскохозяйственная академия, Тверь, Россия;

² Тверской государственный технический университет, Тверь, Россия,

* Корреспондирующий автор (alexej.ganichev[at]yandex.ru)

Аннотация

Проблема независимости случайных событий является одной из самых важных и недостаточно изученных в теории вероятностей. Важность проблемы вызвана массовым применением в практических приложениях допущения о независимости факторов. В статье показаны формулы для вычисления условных вероятностей суммы, произведения событий и противоположного события. Установлены два необходимых и достаточных условия независимости событий. Полученные результаты могут использоваться в интеллектуальных системах принятия решений.

Ключевые слова: событие, условная вероятность, произведение, сумма событий, критерий независимости, фактор, равенство, утверждение.

STOCHASTIC INDEPENDENCE OF COMPLEX EVENTS

Review article

Ganicheva A.V.¹, Ganichev A.V. ^2, *

¹ ORCID: 0000-0002-0224-8945;

² ORCID: 0000-0003-3389-7582;

¹ Tver State Agricultural Academy, Tver, Russia;

² Tver State Technical University, Tver, Russia,

* Corresponding author (alexej.ganichev[at]yandex.ru)

Abstract

The problem of independence of random events is one of the most important and insufficiently studied in probability theory. The importance of the problem is caused by the mass application of the assumption of independence of factors in practical provisions. The article shows formulas for calculating the conditional probabilities of a sum, the product of events and the opposite event. Two necessary and sufficient conditions for the independence of events have been determined. The obtained results can be used in intelligent decision-making systems.

Keyword: event, conditional probability, product, sum of events, independence criterion, factor, equality, statement.

Введение

Многие вероятностно-статистические модели основываются на использовании независимых событий в качестве результатов измерений, наблюдений, испытаний, опытов, анализа данных. Например, в системах распознавания объектов предполагают независимость их характерных признаков, в системах диагностики говорят о независимости появления одного вида дефектов изделий от других видов, при выпуске продукции используют понятие независимости факторных переменных и т.д. Причиной частого использования независимости случайных событий является существенное упрощение математических выкладок по сравнению с зависимыми событиями. Понятие независимости событий носит философски-методологический характер [5]. При этом следует учитывать субъективный и объективный подходы к данному вопросу [3]. Как отмечается в работе [7, С. 463], вероятностный подход является ключевым в современном научном мировоззрении. В научной литературе недостаточно рассмотрены вопросы условных вероятностей и независимости событий.

При использовании основ теории вероятностей возникают две задачи:

1) нахождение условных вероятностей произведения и суммы событий, а также условной вероятности противоположного события;

2) установление критерия независимости событий.

Эти две задачи определяют цель данной статьи.

Постановка задачи

Как отмечается в [4, С. 132], понятие условной вероятности является основным элементом теории вероятностей. А.Н. Колмогоров полагал, что идея независимости является центральной в статистике [10]. В статье [9] описан способ построения вероятностных мер посредством условных относительных мер, относящихся ко всей совокупности наблюдаемых событий.

Условной вероятностью события A при наличии B называется вероятность события A, вычисленная при условии, что событие B произошло. Принято обозначение .

Приведем определение независимых событий, данное в [1], [2], [4]. Событие A называется независимым от B, если его вероятность не зависит от того, произошло событие B или нет, т.е.. В противном случае, если , событие A зависит от B. Сформулируем основные свойства условных вероятностей и докажем критерий независимости сложных событий.

Теоремы об условных вероятностях

Важной задачей, возникающей при работе с условными вероятностями, является нахождение условных вероятностей произведения и суммы событий, а также вероятности противоположного события. Из приведенных ниже соотношений (1)-(8) формулы (1)-(5), (7) отражены в литературе, (6) и (8) не нашли должного отражения.

Теорема 1. Для любых событий  справедливы следующие соотношения:

Доказательство. Соотношения 1 и 2 очевидны; соотношение 3 следует из 1; соотношение 7 вытекает из 1, 8 – из 6.

Доказательство соотношения 6 вытекает из следующей цепочки равенств:

Докажем соотношения 4 и 5. Имеем:

Для несовместных событий:

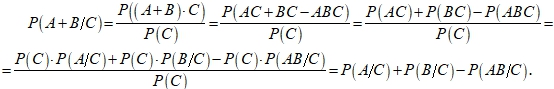
Утверждения 4, 5 доказаны.

Необходимые и достаточные условия независимости

Другая важнейшая задача теории вероятностей – установление критерия независимости событий. Для иллюстрации доказательства независимости воспользуемся определением, что независимые события А и В не имеют попарно общих элементов, а в сумме составляют все пространство элементарных событий [4].

Теорема 2. Первое необходимое и достаточное условие независимости двух событий.

Пусть  (невозможное событие),

Тогда для независимости событий A и B необходимо и достаточно, чтобы либо событие A не зависело от B₁ и B₂, либо событие B не зависело от событий  .

Доказательство. Пусть A не зависит от  .

Следовательно, . А это и означает независимость событий A и B.

Докажем утверждение в обратную сторону. Пусть A и B - независимые события. Найдем

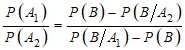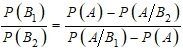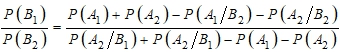Отсюда получаем:     (9) Аналогично получаем равенство:     (10) Предположим, что . Получаем     (11) Представим A  в виде , тогда равенство (12) преобразуется к виду:     (12) Представим A в виде , тогда равенство (12) преобразуется к виду:     (13)

Выразим  из (11) и, подставив в последнее равенство, после преобразования получим

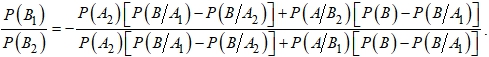
Аналогично, выразим  из (11) и, подставив в (13), после преобразования будем иметь

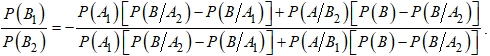
Положим

Тогда, сравнивая правые части выражения , получим

Отсюда: . Преобразуем последнее выражение: .

Отсюда следует, что либо .

В первом случае получаем, что , но это и означает независимость A от B₁ и B₂. Для второго случая имеем:

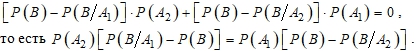
Отсюда с применением равенства (9) получаем, что . Это противоречит условию.

Если , то тогда из условия  следует, что , т.е. B зависит от . Аналогично рассматривается случай, когда . Независимость B от    доказывается таким же способом.

Теорема 2 доказана.

Теорема 3. Второе необходимое и достаточное условие независимости двух событий.

Пусть  (невозможное событие),

Тогда для независимости A и B необходимо  достаточно, чтобы  и  были независимы от  .

Доказательство. Пусть,  не зависят от  . Докажем, что тогда A не зависит от B.

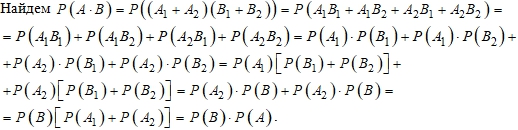
Следовательно, , а это означает независимость событий A и B.

Докажем утверждение в обратную сторону. Пусть A и B - независимые события. Докажем, например, что A₁ не зависит от  .

Поскольку любое событие  связано с действием некоторого фактора G, то это действие можно заменить действием двух факторов  таких, что результаты действия  есть события , соответственно, и такие, что . При этом можно считать действия  независимыми, а поэтому события    также будут независимы.

По условию ,  совместно с , а поэтому действия соответствующих факторов , связанные с этими событиями, также могут произойти вместе. Но тогда L может произойти одновременно с факторами , а в этом случае  может произойти совместно с событиями  . Аналогично доказывается, что  совместно с .

Кроме того, по условию , и можно доказать, что .

В самом деле, поскольку .

Поэтому если , а это возможно только в том случае, когда , а этого не может быть, так как тогда   - противоречит условию.

Нетрудно видеть, что мы оказываемся в рамках предыдущей теоремы. А именно: B не зависит от A₁. Кроме того, совместны с  , т.е. если ; кроме того  .

Отсюда следует, что A₁  не зависит от  . Совершенно аналогично доказываем независимость A₂ от  .

Теорема 3 доказана.

Заключение

На основе условных вероятностей событий строятся Байесовские сети доверия, которые используются для принятия и обоснования решений в системах искусственного интеллекта. Практическое применение полученных результатов заключается в возможности организации корректной обработки больших массивов статистических данных, на основе доказанных в работе теорем. Сложность вычисления вероятностей сложных событий вызывает необходимость их приближенного вычисления.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Ганичева А. В. Теория вероятностей / А. В Ганичева. ‑ Санкт-Петербург: Лань, 2017. – 144 с.
2. Вентцель Е.С. Теория вероятностей / Е.С. Вентцель. – М.: КноРус, 2010. – 664 с.
3. Зепнова Н.Н. Субъективный и объективный подходы к решению задач теории вероятностей и дискретной математики / Н.Н.Зепнова, О.В. Кузьмин // Вестник Бурятского государственного университета. ‑ 2017. ‑ № 7. ‑ С. 196-204.
4. Орлов А.И. Математика случая. Вероятность и статистика – основные факты / А.И. Орлов, М.: МЗ-Пресс, 2004. ‑ 170 с.
5. Резников В.М. Философско-методологический анализ понятия независимости в вероятностной теории причинности и в теории вероятностей / В.М. Резников // Философия науки. ‑ 1998. ‑ № 1.‑ С. 6.
6. Солодухин А. Приближенное вычисление вероятности сложного события в условиях объективной недостаточности статистических опытов / А.Солодухин // Труды Второй Российской конференции молодых ученых по информационному поиску. – Таганрог: Изд-во ТТИ ЮФУ, 2008. – C. 79-89.
7. Татаринов В.В. Замечание об основаниях теории вероятностей /В.В. Татаринов // Вестник Тамбовского университета. Серия: Естественные и технические науки. ‑ 2003. ‑ Т. 8. № 3. ‑ С. 462-464.
8. Феллер В. Введение в теорию вероятностей и её приложения. В 2-х томах. Том 1 / В. Феллер, М.: Мир, 1984. –528 с.
9. Чечулин В. Л. Статьи разных лет: сборник / В.Л. Чечулин; Перм. гос. нац. исслед. ун-т. – Пермь, 2017. — Вып. 4. – 136 с.
10. Cartwright N. False idealizations: A probabilistic threatm to scientific method / N. Cartwright // Philos. Studies, 1995. ‑ V. 77. ‑ N. 3. ‑ P. 339 - 352.

Список литературы на английском языке / References in English

1. Ganicheva A. V. Teorija verojatnostej [Probability theory] / A. V Ganicheva. – Sankt-Peterburg : Lan’, 2017. – 144 p. [in Russian]
2. Ventcel E. S. Teorija verojatnostej [Probability theory] / E. S. Ventcel. – M. : KnoRus, 2010. – 664 p. [in Russian]
3. Zepnova N. N. Subjektivnyj i objektivnyj podhody k resheniju zadach teorii verojatnostej i diskretnoj matematiki [Subjective and objective approaches to solving the problems of probability theory and discrete mathematics] / N. N. Zepnova, O. V. Kuzmin // Vestnik Burjatskogo gosudarstvennogo universiteta [Bulletin of Buryat State University]. –2017. – № 7. – P. 196-204. [in Russian]
4. Orlov A. I. Matematika sluchaja. Verojatnost' i statistika – osnovnye fakty [Mathematical variants. Probability and statistics – the main facts] / A. I. Orlov, M. : MZ-Press, 2004. – 170 p. [in Russian]
5. Reznikov V. M. Filosofsko-metodologicheskij analiz ponjatija nezavisimosti v verojatnostnoj teorii prichinnosti i v teorii verojatnostej [Philosophical and methodological analysis of the concept of independence in the probabilistic theory of causality and in the theory of probabilities] / V. M. Reznikov // Filosofija nauki [The philosophy of Science]. – 1998. – № 1. – P. 6. [in Russian]
6. Soloduhin A. Priblizhennoe vychislenie verojatnosti slozhnogo sobytija v uslovijah objektivnoj nedostatochnosti statisticheskih opytov [The approximate calculation of the probability of a complex event in the conditions of objective insufficiency of statistical experiments] / Soloduhin A. // Trudy Vtoroj Rossijskoj konferencii molodyh uchenyh po informacionnomu poisku [The Materials of the Second Russian Conference of Young Scientists on Information Search] – Taganrog : TTI JuFU, 2008. – pp. 79-89. [in Russian]
7. Tatarinov V. V. Zamechanie ob osnovanijah teorii verojatnostej [The remark on the foundations of probability theory] / V. V. Tatarinov // Vestnik Tambovskogo universiteta. Serija: Estestvennye i tehnicheskie nauki [Bulletin of the University of Tambov. Series: Natural and technical sciences]. – 2003. – Vol. 8. № 3. P. 462-464. [in Russian]
8. Feller V. Vvedenie v teoriju verojatnostej i ejo prilozhenija. V 2 tomah. Tom 1 [Introduction to probability theory and its applications. In two volumes. Vol. 1] / V. Feller, M. : Mir, – 1984. – 528 p. [in Russian]
9. Chechulin V. L. Stat'i raznyh let: sbornik [The collection of articles of different years] / V. L. Chechulin; Perm. gos. nac. issled. un-t [Perm State National Research University]. – Perm', 2017. – Issue. 4. – 136 p. [in Russian]
10. Cartwright N. False idealizations: A probabilistic threat to scientific method / N. Cartwright // Philos. Studies, 1995.  – V. 77. –  N. 3. –  P. 339 - 352.