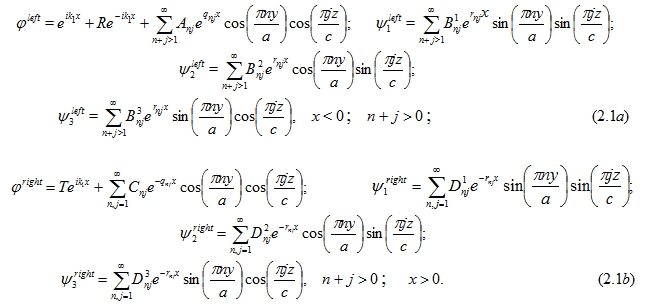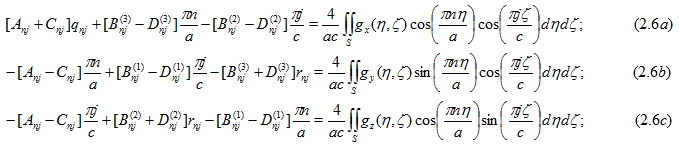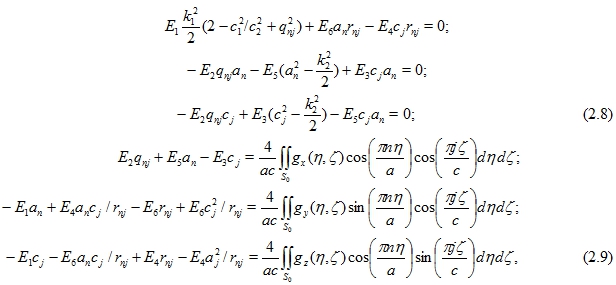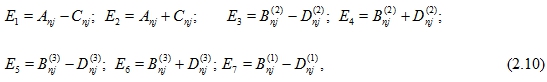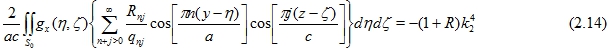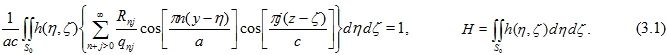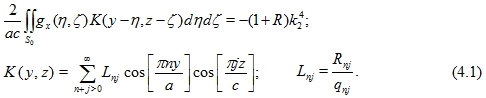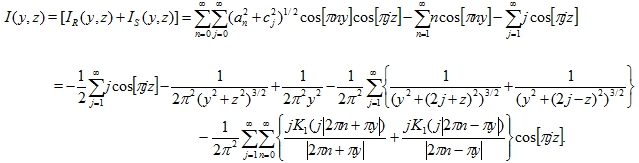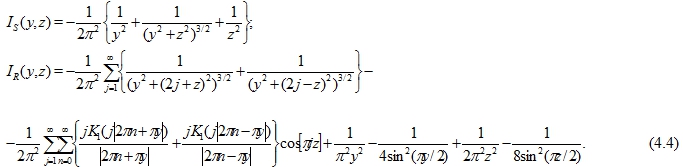НИЗКОЧАСТОТНОЕ ПРОХОЖДЕНИЕ УПРУГИХ ВОЛН ЧЕРЕЗ ДВОЯКОПЕРИОДИЧЕСКУЮ СИСТЕМУ ТРЕЩИН В ТРЕХМЕРНОЙ ПОСТАНОВКЕ
Ремизов М.Ю.
ORCID: 0000-0001-5078-9941 Кандидат физико-математических наук, Ростовский государственный строительный университет
НИЗКОЧАСТОТНОЕ ПРОХОЖДЕНИЕ УПРУГИХ ВОЛН ЧЕРЕЗ ДВОЯКОПЕРИОДИЧЕСКУЮ СИСТЕМУ ТРЕЩИН В ТРЕХМЕРНОЙ ПОСТАНОВКЕ
Аннотация
Данная работа посвящена выводу аналитических выражений для коэффициентов отражения и прохождения, когда плоская волна падает на двумерную решетку с периодическим массивом прямоугольных щелей в упругой изотропной среде в трехмерной постановке. В режиме частотного диапазона одной моды задача сводится к гиперсингулярному интегральному уравнению. Показано, что кроме свойства гиперсингулярности интегрального уравнения обнаружены новые сингулярности по каждой из координат двумерной решетки.
Ключевые слова: коэффициенты отражения и прохождения, двумерная решетка, гиперсингулярное интегральное уравнение.
Remizov M.Yu.
ORCID: 0000-0001-5078-9941, PhD in Physics and Mathematics, Rostov-on-Don State University of Civil Engineering
3D LOW-FREQUENSY PENETRATION OF ELASTIC WAVES THROUGH A DOUBLY PERIODIC ARRAY OF CRACKS
Abstract
The paper is devoted to the calculation of the reflection and transmission coefficients, when a plane wave is incident on a two-dimensional grating with a periodic array of rectangular cracks in the elastic material in 3-D. In the one-mode frequency range the problem is reduced to a single hipersingular integral equation, which leads to an explicit representation of the wave characteristics for various sizes of the cracks. New singularities along each coordinate of two-dimensional grating have been revealed for the obtained hipersingular integral equation of double singularity.
Keywords: the reflection and transmission coefficients, a two-dimensional grating, hipersingular integral equation.
1.Введение. Исследование проникновения упругих волн через периодические решетки является важной проблемой в области ультразвуковой количественной оценки материалов, распространении звука и для электромагнитных волноводов с диафрагмами. Различные численные методы были применены в двумерных задачах с периодическими отверстиями произвольной формы [1-2]. Несмотря на высокую точность компьютерных результатов, существует только несколько аналитических теорий. На практике аналитические результаты могут быть получены в предположении режима низких частот при слабом взаимодействии волн, где некоторые приближенные результаты можно установить в аналитической форме. Таким образом, аналитические методы, обеспечивающие явные формулы для соответствующих параметров рассеяния, задают только определенный низко-частотный предел.
В работах [3-6] получены явные аналитические формулы для параметров отражения и преломления в режиме одной моды для акустической волны, проникающие сквозь двояко-(трояко)-периодические массивы отверстий и объемных препятствий произвольной формы, а также для плоских задач распространения волн через периодический массив экранов в упругих твердых телах. Влияние вязкости на отражение и прохождение акустических волн на периодической решетке экранов для 3-D проблем было рассмотрено в [7].
В настоящей работе мы продолжаем исследование двояко-периодической структуры, расположенной в бесконечной плоскости в 3-D случае. Так же, как в [1-6], мы предполагаем, что при нормальном падении волны имеет место режим распространения одной моды, т.е. ![]() где
где ![]() - волновое число продольной падающей волны
- волновое число продольной падающей волны ![]() . Целью настоящей работы является получение новых аналитических выражений для коэффициентов отражения и прохождения в случае трехмерного распространения и описание новых свойств ядра полученного гиперсингулярного интегрального уравнения.
. Целью настоящей работы является получение новых аналитических выражений для коэффициентов отражения и прохождения в случае трехмерного распространения и описание новых свойств ядра полученного гиперсингулярного интегрального уравнения.
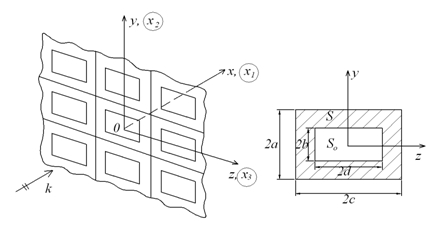
2. Математическая постановка задачи. Рассмотрим среду, которая состоит из бесконечной плоскости x=0, содержащую двумерный бесконечный периодический массив трещин, с периодами по осям y и z 2a и 2c соответственно. Если мы изучаем падение плоской волны на решетку вдоль положительного направления оси x, то в силу симметрии вопрос сводится к рассмотрению волновода ширины 2a вдоль оси y и 2c вдоль оси z, (рис.1). Следовательно, если падающая волна единичной амплитуды, как предполагается, распространяются нормально к плоскости x=0, то потенциалами Ламэ, удовлетворяющие уравнению Гельмгольца, являются следующие функции:
Рис.1 Распространение падающей волны через периодический массив просветов.
Заглавные буквы здесь являются неизвестными константами и
гармонической временной множитель берется в виде ![]() , являются продольным и поперечным волновыми числами, а R,T - коэффициенты отражения и прохождения, соответственно. Далее возьмем компоненты тензора напряжений
, являются продольным и поперечным волновыми числами, а R,T - коэффициенты отражения и прохождения, соответственно. Далее возьмем компоненты тензора напряжений ![]() и вектора перемещений в терминах потенциалов, используя стандартные формулы Грина-Ламэ.
и вектора перемещений в терминах потенциалов, используя стандартные формулы Грина-Ламэ.
Потенциалы ![]() должны удовлетворять дополнительному условию
должны удовлетворять дополнительному условию
![]()
В рассматриваемой задаче плоская продольная волна с потенциалами
приходит из ![]() , и порождает отраженное поле. Предполагая непрерывность поля перемещений
, и порождает отраженное поле. Предполагая непрерывность поля перемещений ![]() вне трещин, введем следующий вектор неизвестных функций
вне трещин, введем следующий вектор неизвестных функций ![]()
Используя (2.1),(2.3), получим все необходимых постоянные, входящие в потенциалы (2.1) в терминах ![]() . Интегрируя уравнения (2.4) по области
. Интегрируя уравнения (2.4) по области ![]() , имеем
, имеем
Свойство ортогональности тригонометрических функций приводит уравнения (2.4),(2.5) к соотношениям
Условия непрерывности напряжений на на границе, имеют место в виде
После применения для (2.7) аналогичной процедуры интегрирования по области ![]() и, принимая во внимание свойство ортогональности тригонометрический функций, получим с учетом (2.6) систему
и, принимая во внимание свойство ортогональности тригонометрический функций, получим с учетом (2.6) систему
и обозначено ![]() . Линейная алгебраическая система шестого порядка относительно
. Линейная алгебраическая система шестого порядка относительно ![]() (2.9) учитывает условие (2.3b) в виде
(2.9) учитывает условие (2.3b) в виде
Решение этой системы определяет постоянные ![]() , три из которых для
, три из которых для ![]() , используемых ниже, принимают вид
, используемых ниже, принимают вид
Теперь мы можем получить все неизвестные константы, взятые из (2.8)-(2.12) и использовать эти значения в условиях равенства нулю компонент напряжений (2.7) на трещине. Здесь мы должны принять во внимание, что в задаче остается только одна нетривиальная функция раскрытия ![]() , входящая в соотношение
, входящая в соотношение
Опуская некоторые рутинные математические преобразования окончательно получаем следующее интегральное уравнение для этой функции ![]() :
:
где числитель выражения ядра принимает форму функции Рэлея
3. Аналитические выражения волновых характеристик. Так же как и в [3], рассмотрим вспомогательное уравнение
В терминах четной функции из (2.5) и (2.14) получаем:
где было обозначено
После интегрирования уравнения (3.2) по области ![]() получаем линейное алгебраическое уравнение, решив которое имеем
получаем линейное алгебраическое уравнение, решив которое имеем
Как только ![]() определены находим все необходимые параметры и волновые характеристики. Коэффициенты отражения и преломления будут выражаться так
определены находим все необходимые параметры и волновые характеристики. Коэффициенты отражения и преломления будут выражаться так
4. Свойства интегрального уравнения. Начнем с рассмотрения символа ядра полученного интегрального уравнения ![]()
Заметим, что ![]() Тогда, сумма составляющая ядро преобразуется к виду
Тогда, сумма составляющая ядро преобразуется к виду
Сейчас первая сумма ядра есть некоторая регулярная функция. Вторая имеет как регулярную, так и и сингулярную части. В результате выделения регулярной и сингулярной части при ![]() и, опустив далее знак тильды, приходим к представлению
и, опустив далее знак тильды, приходим к представлению
где ![]() преобразуется к виду, используя формулу суммирования Пуассона
преобразуется к виду, используя формулу суммирования Пуассона
Здесь ![]() функция Макдональда (первого рода). В итоге получаем сингулярную и регулярную части соответственно
функция Макдональда (первого рода). В итоге получаем сингулярную и регулярную части соответственно
В заключение необходимо отметить, что полученная двойная сингулярность имеет место наряду с сингулярностью по каждой из переменной в отдельности. Для анализируемой задачи такая особенность была обнаружена впервые. Стабильность при двумерной сингулярности гиперсингулярных интегральных уравнений доказана, тогда как стабильность всей ![]() с учетом сингулярности по каждой из координат пока доказанной не является. Сейчас мы проводим расчетные эксперименты для выявления сути новой комбинированной сингулярности.
с учетом сингулярности по каждой из координат пока доказанной не является. Сейчас мы проводим расчетные эксперименты для выявления сути новой комбинированной сингулярности.
Литература
- Ахенбах Дж. Ди., Ли З.Л. Отражени е и передача скалярных волн периодической системой экранов, Движение волны.-1986.-№8.,-225-234.
- Майл Дж.. Релеевское рассеяние решеткой. Движение Волны.-1982-№4.- 285-292.
- Скарпетта Э., Сумбатян М. А. Явные аналитические результаты для одно-модового режима проникновения в периодической систему экранов, Журнал ИМА прикладной математики.-1996. -№56. -109-120.
- Скарпетта Э., Сумбатян М. А. Низкочастотные проникновения акустических волн через периодические решетки произвольные формы: трехмерная задача, Движение волны.-1995.-№22.- 133-144.
- Скарпетта Э., Сумбатян М. А. О распространении волн в упругих средах через массив щелей двойной периодический, Движение волны.-1997.- №25, 61-72.
- Скарпетта Э., Тибуло В. Трехмерное распространение волн через каскадные экраны с периодической системой произвольных отверстий, Инт. Дж. Англ. ТСМ.-2008. -№46, 105-111.
- Хоментковши Д., Майлз Р.Н. Влияние вязкости дифракции звука на периодической системе экранов. Общие 3-д проблемы, Дж. журнал. Соц. Я.- 2005.- № 117(5), 2761-2771.
References
- Achenbach J.D. , Li Z.L. Reflexion and transmission of scalar waves by a periodic array of screens, Wave Motion.-1986.-№ 8.-, 225-234.
- Miles J.W. On Rayleigh scattering by a grating. Wave Motion.-1982-№4.- 285-292.
- Scarpetta E., Sumbatyan M.A. Explicit analytical results for one-mode oblique penetration into a periodic array of screens, IMA Journal of Applied Mathematics.-1996.-№56.- 109-120.
- Scarpetta E., Sumbatyan M.A. Low-frequency penetration of acoustic waves through a periodic arbitrary-shaped grating: the three-dimensional problem, Wave Motion.-1995.-№22.- 133-144.
- Scarpetta E., Sumbatyan M.A. On wave propagation in elastic solids with a doubly periodic array of cracks, Wave Motion.-1997.- №25, 61-72.
- Scarpetta E., Tibullo V. On the three-dimensionl wave propagation through cascading screens having a periodic system of arbitrary openings, Int. J. Eng. Sci.-2008.-№46, 105-111.
- Homentcovschi D., Miles R.N. Influence of viscosity on the diffraction of sound by a periodic array of screens. The general 3-D problem, J. Acoust. Soc. Am.- 2005.- № 117(5), 2761-2771.