КОЭФФИЦИЕНТ ЭФФЕКТИВНОСТИ ОКОННОГО СПЕКТРАЛЬНО-СТАТИСТИЧЕСКОГО МЕТОДА ДЕТЕКТИРОВАНИЯ СИГНАЛОВ В ШУМЕ

Останин С.А.¹, Семёнов Г.А.²_, Шайдук А.М.³

¹Кандидат физико-математических наук, Алтайский государственный университет, ООО "АГФЗ", ²Кандидат физико-математических наук, Санкт-Петербургский государственный аграрный университет, ³Доктор физико-математических наук, Алтайский государственный медицинский университет

КОЭФФИЦИЕНТ ЭФФЕКТИВНОСТИ ОКОННОГО СПЕКТРАЛЬНО-СТАТИСТИЧЕСКОГО МЕТОДА ДЕТЕКТИРОВАНИЯ СИГНАЛОВ В ШУМЕ

Аннотация

Описан способ увеличения чувствительности детектирования коротких периодических сигналов в гауссовском шуме, основанный на разделении исследуемой аддитивной смеси сигнала и шума на фрагменты с использованием временного окна. Получена функциональная зависимость значения универсального спектрального критерия детектирования от количества участков разделения исследуемого временного ряда. Введён коэффициент эффективности оконного спектрально-статистического метода, позволяющий определить оптимальное количество участков разделения аддитивной смеси сигнала и шума, необходимое для успешного детектирования сигнала.

Ключевые слова: оконный спектрально-статистический метод, детектирование сигналов в шуме.

Ostanin S.A.¹, Semenov G.A.², Shayduk A.M.³

¹PhD in Physics and Mathematics, Altai state University, ²PhD in Physics and Mathematics, Saint-Petersburg state agrarian University, ³PhD in Physics and Mathematics, Altai state medical university

EFFICIENCY RATIO OF WINDOW SPECTRAL-STATISTICAL METHOD FOR DETECTION SIGNAL IN NOISE

Abstract

The described method of increasing the sensitivity of the detection of short periodic signals in Gaussian noise based on separation of the additive mixture of signal and noise into fragments using a time window. The obtained function of the spectral values a universal criterion for the detection of the number of sections separating the studied time array. Introduced the efficiency factor of the window a spectral-statistical method to determine the optimal number of segments separating an additive mixture of signal and noise necessary for successful signal detection.

Keywords: spectral-statistical window method, detection signal in noise.

С целью повышения чувствительности спектрального детектирования квазипериодических сигналов в гауссовском шуме необходимо исследование возможностей расширения границ его применимости, для чего рассмотрим этапы создания оконного спектрально-статистического метода, основанного на статистическом методе спектрального детектирования [1‑2].

Рассмотрим аддитивную смесь:

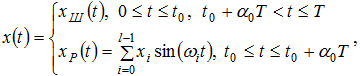 (1)

где среднее квадратическое отклонение шумовой компоненты _Ш(t) равно σ_Ш, относительная длительность квазипериодического сигнала равна α₀. Временной ряд, полученный из (1) – числовая последовательность , представляющая собой сигнал (t), измеренный в точках . Число элементов N этой последовательности будем считать достаточно большим, то есть N» 1. Число членов временного ряда, соответствующего квазипериодической части сигнала равно . Из анализа критерия обнаружения квазипериодического сигнала статистическим методом спектрального детектирования [2]:

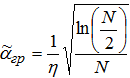 (2)

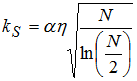и выражения для универсального спектрального критерия [3]:  (3)

можно увидеть, что допустимая относительная длительность квазипериодической части сигнала  линейно убывает с увеличением его относительной мощности  при неизменном объёме выборки N и пропорциональна величине 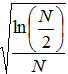 при изменении объёма выборки. Ясно, что если шумовой участок суммарного сигнала статистически однороден на всей временной области его существования, то значение величины η  не зависит от временного интервала, на котором производилось её вычисление.

С учётом того, что величина относительной длительности квазипериодической части зависит от длительности случайной компоненты сигнала, рассмотрим возможные пути увеличения параметра α посредством разбиения исследуемого суммарного сигнала (1) с помощью временного окна на фрагменты (подмассивы в дискретном случае) и последующего построения их спектров и дальнейшего анализа.

В связи с тем, что разбиение сигнала на фрагменты является линейной операцией, рост величины α также будет линейным. Так как при этом уменьшается объём временного ряда, будет увеличиваться граничное значение относительной длительности квазипериодического сигнала  α_гр пропорционально множителю 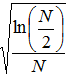, что частично ухудшит возможности детектирования, однако общая тенденция повышения чувствительности при этом сохранится. Разбиение рассматриваемого временного ряда на подмассивы следует проводить таким образом, чтобы величина шага сдвига временного окна равнялась половине размера окна. Это требуется для того, чтобы в процессе разбиения временного ряда квазипериодическая компонента полностью содержалась бы в одном из подмассивов и при детектировании учитывалась вся её энергия.

Для определения возможностей оконного спектрального подхода далее проведём оценку его эффективности по сравнению со статистическим методом спектрального детектирования.

Разделим массив Χ_i на (2n-1) подмассивов так, чтобы сдвиг временного окна составлял половину его ширины (объём подмассивов равен размеру временного окна):

 (4)

где Y_jk – k-тый член j-того подмассива. Значения индексов меняются в диапазонах: . Величина   – размер временного окна. При разбиении временного ряда по правилу (4) каждый подмассив представляет собой j-тую строку матрицы:

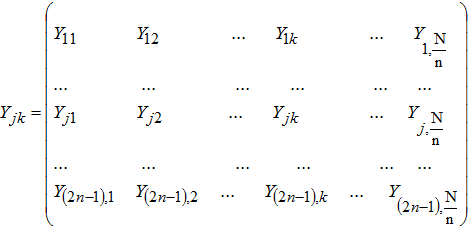 (5)

С учётом гипотезы о соотношении длительности квазипериодической компоненты и размера временного окна, принятой ранее, будем считать, что квазипериодический участок сигнала полностью содержится в одном из подмассивов рассматриваемого временного ряда после разделения. То есть теперь для некоторой строки Y_j будет проверяться критерий спектрального детектирования статистическим способом, который ранее применялся ко всему временному ряду Χ_i. Запишем результаты, полученные для статистического метода спектрального детектирования применительно к некоторому единственному подмассиву Y_j.

Объём фрагмента сигнала Y_j равен, с учётом чего относительная длительность квазипериодического сигнала α_Y для временного ряда Y_j запишется теперь как

 (6)

то есть получаем линейный рост α_Y пропорционально увеличению количества участков разбиения (параметра n). Пороговое значение длительности квазипериодической компоненты , при котором теперь реализуемо его успешное обнаружение в нормальном шуме в пределах временного окна, с учётом (1) равно:

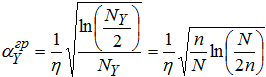 (7)

Значение относительной мощности квазипериодической части сигнала  сохраняется при этом неизменным. Условие успешного детектирования квазипериодической компоненты теперь выражается соотношением:

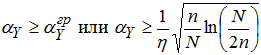  (8)

Переходя от (8) к условию для α₀ с учётом (6), получаем:

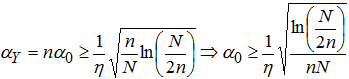  (9)

то есть пороговое значение относительной длительности квазипериодической части сигнала при его детектировании в нормальном шуме оконным спектральным методом по отношению ко всему сигналу (1) равно:

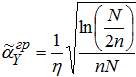  (10)

Универсальный спектральный критерий оценки квазипериодического сигнала на предмет возможности его обнаружения в нормальном шуме примет вид:

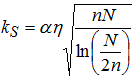  (11)

Отношение ξ величин пороговых значений относительной длительности квазипериодической компоненты, требуемых для их успешного обнаружения, соответствующих статистическому методу спектрального детектирования (2) и оконному спектральному методу (11) определим как коэффициент эффективности оконного метода:

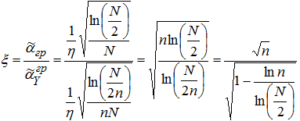 (12)

Коэффициент эффективности ξ определяет число фрагментов разбиения рассматриваемого временного ряда, при котором реализуемо успешное детектирование квазипериодической компоненты в одном из участков. Определим из (12) значение параметра n при фиксированных значениях ξ:

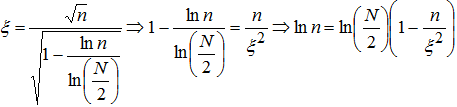  (13)

Численно решаем уравнение (13) относительно n, находим значение n₀, число фрагментов разбиения сигнала при этом определяется как:

   (14)

С целью поиска оптимального значения параметра , соответствующего наиболее эффективному для успешного детектирования квазипериодического сигнала количеству разбиений временного ряда Χ_i, проведём исследование функции ξ(n) на наличие экстремумов.

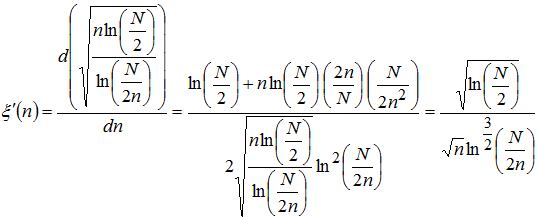 (15)

Из (15) видно, что на рассматриваемом интервале производная ξ(n)  нулей не имеет, всюду положительна, то есть функция ξ(n) возрастает на всей её области определения. При этом ξ(n) имеет область значений:

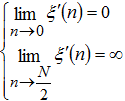  (16)

Понятно, что значение параметра  практически не реализуемо, так как ширина временного окна при этом должна составлять всего два элемента; однако, на всей практически осуществимой области изменения параметра n эффективность оконного метода растёт при увеличении числа фрагментов разбиения сигнала. Верхняя граница параметра n определяется минимальным количеством членов временного ряда, требуемым для корректного задания квазипериодической части и возможностью обнаружения этого сигнала посредством построения его спектра. Также она определяется длительностью квазипериодической компоненты: при завышенном числе фрагментов разбиения сразу несколько подмассивов временного ряда будут составлять квазипериодический участок, что не является необходимым и, более того, потребует выполнения некоторого количества лишних вычислительных операций. Таким образом, применение оконного спектрального метода детектирования при уменьшении относительной длительности квазипериодической компоненты α₀ требует увеличения коэффициента эффективности ξ, что в свою очередь требует увеличения числа фрагментов разбиения сигнала.

Главным препятствием здесь является то, что при большом увеличении числа фрагментов разбиения сигнала несколько повышается вероятность ошибочного детектирования, то есть эффективность оконного метода в вероятностном смысле несколько снижается.

Литература

1. Семёнов Г.А. Поиск сигнала в нормальном шуме методом анализа статистики спектра / Г.А. Семёнов // Известия Алтайского госуниверситета. – 2011. – Ч.1(69) – С. 189 191.
2. Семёнов Г.А. Выявление порога чувствительности спектрального метода к поиску периодического сигнала в нормальном шуме / Г.А. Семёнов // Известия Алтайского госуниверситета. – 2011. – Ч.1(69) – С.192 196.
3. Семёнов Г.А. Универсальный спектральный критерий возможности детектирования периодических сигналов в нормальном шуме / С.А. Останин, Г.А. Семёнов, А.М. Шайдук // Труды конференции "Лазеры. Измерения. Информация". – СПб: Изд-во СПб государственного политехнического университета. – 2011. – С.4 5.

References

1. Semjonov G.A. Poisk signala v normal'nom shume metodom analiza statistiki spektra / G.A. Semjonov // Izvestija Altajskogo gosuniversiteta. – 2011. – Ch.1(69) – S. 189 191.
2. Semjonov G.A. Vyjavlenie poroga chuvstvitel'nosti spektral'nogo metoda k poisku periodicheskogo signala v normal'nom shume / G.A. Semjonov // Izvestija Altajskogo gosuniversiteta. – 2011. – Ch.1(69) – S.192 196.
3. Semjonov G.A. Universal'nyj spektral'nyj kriterij vozmozhnosti detektirovanija periodicheskih signalov v normal'nom shume / S.A. Ostanin, G.A. Semjonov, A.M. Shajduk // Trudy konferencii "Lazery. Izmerenija. Informacija". – SPb: Izd-vo SPb gosudarstvennogo politehnicheskogo universiteta. – 2011. – S.4 5.