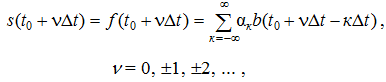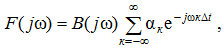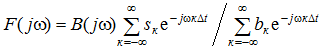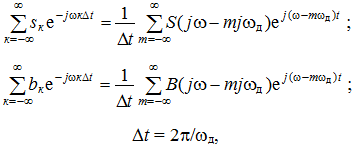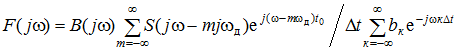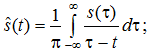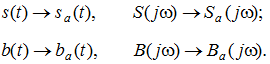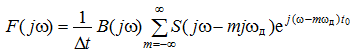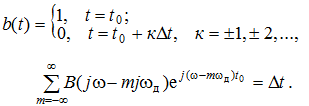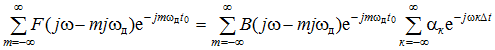РАВНОМЕРНАЯ ИНТЕРПОЛЯЦИЯ ПРИ ВОССТАНОВЛЕНИИ СИГНАЛОВ

Захарченко Н.В. ¹, Бектурсунов Д.Н. ², Севастеев Е.А. ³, Гавель С.Н. ⁴

¹Доктор технических наук, ²Аспирант, ³Аспирант, ⁴Аспирант, Одесская национальная академия связи

РАВНОМЕРНАЯ ИНТЕРПОЛЯЦИЯ ПРИ ВОССТАНОВЛЕНИИ СИГНАЛОВ

Аннотация

Рассматриваются различные вопросы интерполяции сигналов при приближенных представлениях их: интерполяция аналитических сигналов и сигналов с ограниченным спектром.

Ключевые слова: интерполяция, аналитические сигналы, сигналы с ограниченным спектром.

Zakharchenko N.V. ¹, Bektursunov D.N. ², Sevasteev E.A. ³, Gavel S.N. ⁴

¹Ph.D., ²Graduate, ³Graduate, ⁴ Graduate, Odessa National Academy of Telecommunications;

UNIFORM INTERPOLATION AT RESTORATION OF SIGNALS

Abstract

Various questions of interpolation of signals at their approximate representations are considered: interpolation of analytical signals and signals with a limited range.

Keywords: interpolation, analytical signals, signals with a limited range.

Постановка задач и решение. Пусть s(t) и b(t) – произвольные (вещественные либо комплексные) сигналы со спектрами s(jw) и В(jw)  соответственно. Приблизим s(t) суммой

               (1)

так, чтобы строго выполнялось равенство

               (2)

где Δt – произвольный заданный шаг интерполяции,  t₀ – произвольный начальный момент отсчета.

Согласно (2), необходимо интерполировать сигнал s(t) суммой f(t) на бесконечной равномерной сетке узлов t₀ + νΔt  (n = 0, ±1, ±2, ...).

Допустим, что равенство (2) выполняется и, исходя из этого, определим погрешность приближения s(t) суммой f(t) на бесконечной непрерывной оси времени.

Перепишем равенство (2) в форме

               (3)

где  s_ν = s(t₀ + νΔt),   b_ν–к  = b(t₀ + ννΔt – кΔt). С использованием двустороннего

z-преобразования это равенство запишем в виде

               (4)

где z^–1 = е^–рΔt – оператор задержки,  р = σ + jw – комплексная частота;

Здесь В (z^–1) и S (z^–1) – z-преобразования сигналов b(t) и s(t).

Прямое преобразование Фурье равенства (1) дает

               (5)

где F(jw) – спектр f(t).

В плоскости z на окружности единичного радиуса (z = e^–jwΔt), согласно (3) или (4),

               (6)

С учетом этого равенства выражение для F(jw) (5) принимает вид

Согласно формуле суммирования Пуассона [1], справедливы равенства

поэтому окончательно

               (7)

Если b(t) – конечная или бесконечная (по длительности) функция с небольшим количеством ненулевых значений b_к = b(t₀ + кΔt) (например, b(t) – сигнал конечной длительности, сплайн-функция невысокого порядка, парциально- кодированный сигнал и т. д.), то F(jw) удобно представлять в виде

               (8)

Полученные выражения (7) и (8) дают спектр интерполирующей суммы f(t). Погрешность интерполяции определяется

Аналитические сигналы. Как подчеркивалось выше, на сигналы s(t) и b(t) никакие ограничения не накладываются. Считаем, что s(t) и b(t) – вещественные сигналы и образуем на их основе аналитические (комплексные) сигналы

с односторонними спектрами s_а(jw) = 2S₊(jw) и В_а(jw) = 2В₊(jw) соответственно. Здесь ŝ(t) и ̂ b(t) – преобразования Гильберта [2] сигналов s(t) и b(t),

ĝ(t) определяется аналогично. Нижние индексы + указывают, что используются части спектров, расположенные в области положительных частот.

Все вышеприведенные рассуждения остаются в силе, если в выражениях (1) … (8) проделать замены

 

Сигналы с ограниченным спектром. Допустим, что s(t) и b(t) – низкочастотные сигналы с ограниченным частотой w_с спектрами [3],

Выберем w_д≥2w_с (w_д = 2π/Δt). Из выражения (7) вытекает, что если |B(jw)| не обращается в нуль на тех частотах, на которых |S(jw)| не равен нулю, то E(jw)=0 для всех частот. Если же |B(jw)| и |S(jw)| обращаются в нуль на некоторых частотах, то их необходимо считать малыми величинами одного порядка малости. С учетом этих оговорок справедлив вывод о том, что один заданный сигнал с ограниченным спектром можно интерпoлировать с нулевой погреш­ностью взвешенной суммой запаздывающих сигналов, полученных из дру­го­го заданного сигнала с той же, что и у исходного сигнала, шириной спектра.

Определение весовых коэффициентов интерполирующего ряда. Укажем различные приемы нахождения коэффициентов α_к с учетом выполнения равенства (2).

1. На основе решения бесконечной системы линейных уравнений (3).
2. Как следует из (6), коэффициенты α_к – это коэффициенты Фурье функции

               (9)

либо равной ей функции

               (10)

раскладываемой в ряд Фурье на отрезке [–1/2(w_д);  1/2(w_д)], w_д = 2π/Δt.

Возможные случаи упрощения определения α_к:

1. Сигнал b(t) – конечный по длительности,

тогда, согласно (6), α_к = s_к/b₀. В этом случае выражения (7) и (8) упрощаются:

               (11)

2. Сигнал b(t) является сигналом Найквиста,

               (12)

В этом случае

               (13)

а F(jw) определяется согласно (11).

Представляет интерес случай, когда значения α_к выбираются по формуле (13) при произвольном заданном сигнале b(t), не удовлетворяющем перечисленным случаям 1 и 2. В этом случае сумма f(t) (1) не является интерполирующей, однако ее спектр F(jw) находится по выражению (11).

Условия совпадения линейных преобразований сигналов на бесконечной дискретной равномерной сетке времени. Пусть s(t) и х(t) – произвольные сигналы со спектрами s(jw) и Х(jw). Эти сигналы совпадают на бесконечной равномерной сетке времени

только в том случае, если их спектры удовлетворяют равенству [3]

               (14)

Это равенство может быть использовано для вывода выражения (7). Действительно, если выполняется (2), то выполняется, согласно (14), и равенство

С учетом (5),

Определив из последних равенств сумму  и подставив ее в (5), приходим окончательно к (7), что и требовалось показать.

Литература

1. Кисель В.А. Восстановление сигналов по преобразованным отсчетам // Труды УНИИРТ – Одесса: изд. УНИИРТ. 1995. Вып.1. С. 24-25.
2. Сукачев Э.А. Новая форма представления селективных сигналов для телекоммуникационных систем // Працi УНДIРТ. – Одеса: вид. УНДIРТ. – 1998. № 2 (14). – С. 98-102.
3. Галлагер Р. Теория информации и надежная связь: Пер. с англ. / Под ред. М.С. Пинскера и Б.С. Цыбакова. – М.: Сов. Радио, 1974. – 304 с.

References

1. Kisel V.A. Restoration of signals on the transformed counting // Works UNIIRT – Odessa: prod. UNIIRT. 1995. Publ.1. Page 24-25.
2. Sukachev E.A. A new form of representation of selective signals for telecommunication systems // Pratsi of UNDIRT. – Odessa: look. UNDIRT. – 1998. No. 2 (14). – Page 98-102.
3. Gallager R. Theory of information and reliable communication: The lane with English / Under the editorship of M.S. Pinsker and B.S. Tsybakov. – M.: Owls. Radio, 1974. – 304 pages.