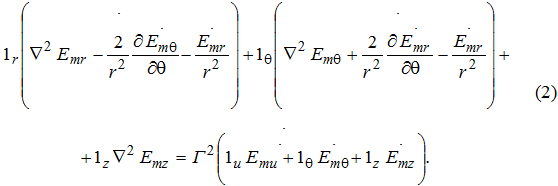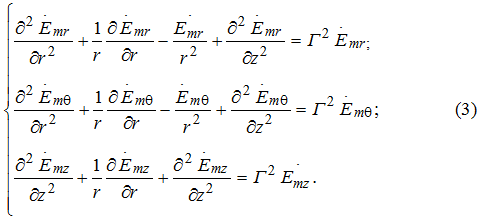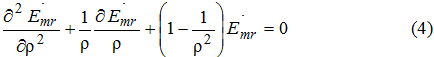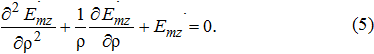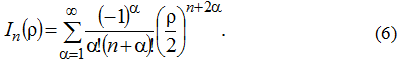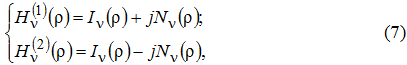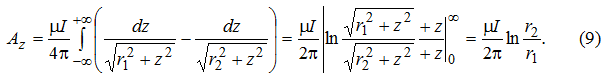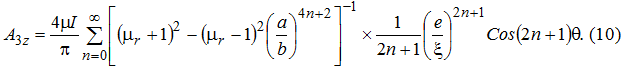ОПРЕДЕЛЕНИЕ ВИДА ПОВРЕЖДЕНИЯ СИЛОВОГО КАБЕЛЯ ПО КОНФИГУРАЦИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

Султанов Георгий Ахмедович¹, Сазыкин Василий Георгиевич², Кудряков Александр Георгиевич³

¹Доктор технических наук, профессор, ²Доктор технических наук, профессор, ³кандидат технических наук, доцент, Кубанский государственный аграрный университет

ОПРЕДЕЛЕНИЕ ВИДА ПОВРЕЖДЕНИЯ СИЛОВОГО КАБЕЛЯ ПО КОНФИГУРАЦИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

Аннотация

Рассматриваются аналитические выражения для определения информационных признаков видов повреждений силовых кабелей. Получены графические образы конфигурации электромагнитного поля, позволяющие однозначно определить место и классифицировать причину повреждения.

Ключевые слова: силовой кабель, электромагнитное поле, информационный признак вида повреждения, графический образ.

Sultanov Georgy Achmedovich¹, Sazykin Vasily Georgievich², Kudryakov Alexander Georgievich³

¹PhD in Engineering, Professor, ²PhD in Engineering, Professor, ³PhD in Engineering, Associate Professor, Kuban State Agrarian University

DETERMINATION OF THE FORM OF DAMAGE TO THE POWER CABLE ON THE CONFIGURATION OF THE ELECTROMAGNETIC FIELD

Abstract

Several analytical expressions to determine the information signs types of damage power cables. Obtained graphic images of the configuration of the electromagnetic field that uniquely define a place and classify the cause of the damage.

Keywords: power cable, electromagnetic field, information is a sign of the damage, graphic means.

В электроснабжении промышленных, городских и сельскохозяйственных объектов напряжением 6–10 кВ, выполненных силовыми кабелями, наблюдается устойчивая тенденция к увеличению их протяженности в связи с концентрацией предприятий в крупных населенных пунктах и городах, для которых кабельные линии (КЛ) являются основным видом распределительных электрических сетей. Кроме того, воздушные линии электропередачи из-за использования больших земельных площадей постепенно замещаются КЛ. По статистическим данным 1980–1990 гг., удельная повреждаемость КЛ 6–10 кВ в СССР составляла в среднем 3,5–7 на 100 км. В настоящее время большая часть имеющихся силовых КЛ эксплуатируются уже более 25 лет и характеризуются повышенной степенью технологических нарушений. Удельное количество повреждений, связанных с последующим ремонтом КЛ, составляет порядка 32/100 км в год, что превышает справочный показатель 7,5/100 км в год более чем в 4 раза [1–3]. В этих условиях возрастает роль технической диагностики при обслуживании и ремонтах КЛ.

Оценка технического состояния изоляции КЛ с применением современных диагностических методов может быть выполнена различными способами [4]. Тем не менее, продолжается разработка новых методов и устройств диагностики. В связи с развитием компьютерной техники, позволяющей быстро выполнять сложные вычисления, появилась возможность непосредственного использования графической модели из классического математического аппарата теории электромагнитного поля (ЭМП) [5–7] для идентификации места и вида повреждения силового кабеля. Кроме того, схемы электроснабжения имеют определенные значения параметров, за счет управления которыми [8] можно выделять и усиливать диагностические признаки для однозначного распознавания повреждений.

В статье приводится один из вариантов способа распознавания отказа по конфигурации ЭМП над местом повреждения силового кабеля.

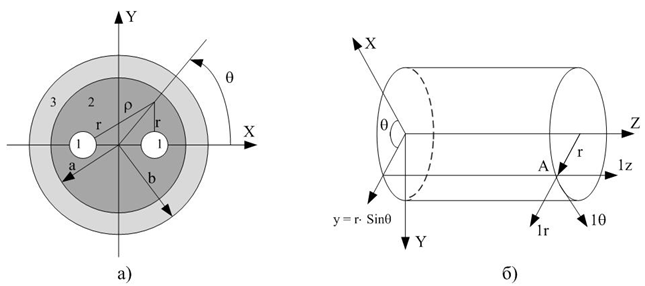
Рассмотрим такие режимы и значения управляющих параметров, при которых характерные диагностические признаки повреждений получают наибольшее разрешение в силовых КЛ с электромагнитным экранами (рис. 1, а). Между проводниками кабеля 1, изоляционной оболочкой 2 и броней 3 находится среда, у которой ЭМП каждого из слоев в случае плоской, поляризованной, монохроматической волны, падающей на поверхность 1, подчиняется условиям [5–7]:

где ∇ – набла-оператор;  – амплитуда вектора напряженности электрического поля;  – оператор Гамильтона; j – показатель мнимой части; ω – круговая частота тока; γ=1/ρ – удельная проводимость среды; μ – магнитная проницаемость среды,

Рис. 1 – Эквивалентное представление участка кабельной линии: а – кабель с экраном; б – система координат для расчета ЭМП.

Для полупроводящих сред уравнение в цилиндрических координатах (рис. 1, б) имеет вид

Отдельные скалярные уравнения в цилиндрических координатах выделить трудно. Если принять допущение, что имеет место осевая симметрия векторов поля, т.е.  то в этом случае получим систему трех скалярных уравнений в системе прямоугольных координат

Уравнения (3) можно решить методом разделения переменных, если применить подстановку  и произвести соответствующие преобразования. В случае, когда поле зависит только от одной переменной r (при параметрическом управлении процессом в целях диагностики), т.е. , тогда, подставляя новую комплексную переменную,  получаем два типа уравнений Бесселя для  и 

и для E_mz

Общее решение (4) может иметь вид

Общее решение (5) может иметь вид

где I₁(ρ) и I₀(ρ) – функции Бесселя первого рода и нулевого порядка; N₁(ρ) и N₀(ρ)  – функции Бесселя второго рода, первого и нулевого порядка, называемые функциями Неймана; H₁⁽¹⁾(ρ) и H₁⁽²⁾(ρ) – взаимно сопряженные функции Ханкеля первого порядка; H₁⁽¹⁾(ρ) H₀⁽¹⁾(ρ), H₀⁽²⁾(ρ) – взаимно сопряженные функции Ханкеля нулевого порядка.

Функция Бесселя n-го порядка для целых чисел  является суммой ряда

Функции Ханкеля, называемые также функциями Бесселя третьего рода, связаны с функциями Бесселя и Неймана уравнениями

где ν=n+1/2 – индекс функции Ханкеля.

Значение функций H_v(ρ) Ханкеля для практического применения заключается в том, что среди функций Бесселя только они приобретают нулевые значения при бесконечных значениях комплексного аргумента, а именно: H⁽¹⁾, – когда мнимая часть является положительной и H⁽²⁾, – когда она отрицательна. В противоположном случае обе функции растут до бесконечности.

В рассматриваемом практическом приложении для диагностики повреждения силового кабеля это значит, что при контроле значений амплитуд гармонических составляющих спектра смена знака амплитуды выражает изменение фазы. Получаемый графический образ может быть использован как информационный признак при распознавании повреждения.

Для векторного магнитного потенциала  А тока i определим характеристики ЭМП снаружи цилиндрического экрана кабеля (рис. 1, а), имеющего магнитную проницаемость μ и охватывающего проводники 1,

Векторный потенциал двухпроводной линии будет иметь только составляющую A_z, направленную перпендикулярно плоскости (рис. 1, б):

Применяя так называемые круговые гармоники, полученные на основании уравнений (5), получим выражение для векторного потенциала в третьей области 3 (рис. 1, а).

Магнитное поле кабеля определяется на основании соотношения B=rot A выраженного в цилиндрических координатах,

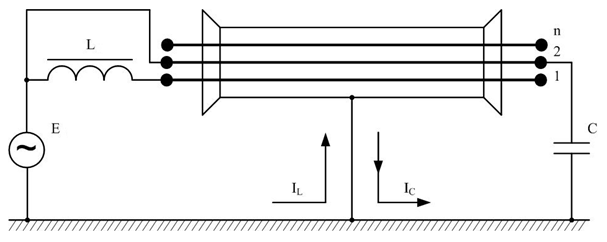
Таким образом, для схемы управляемых параметров (рис. 2) в месте повреждения кабеля требуется организовать растекание токов, формирующих пространственную структуру поля, определяемую природой токов (видом реактивности L и C).

Рис. 2 – Схема включения индуктивности L и C емкости при поиске повреждения изоляции одной из жил кабеля относительно земли

Поиск повреждений [8] можно производить при рабочем напряжении на частоте промышленной 50 Гц, когда за счет тока компенсатора (конденсатора С) индуктивной составляющей (дросселя L) в месте повреждения изоляции формируются амплитудно-фазовые соотношения характеристик поля (значения амплитуд спектрального состава тока замыкания на землю и спектральная плотность мощности).

Ток, возвращающийся через землю, стремится приблизиться к проводнику и не может произвольно распространяться в земле. В результате фазового и пространственного смещения намагничивающих сил поле рассеяния КЛ имеет характер сложной волны, бегущей вдоль оси кабеля. Как показали эксперименты, при отыскании мест повреждения кабеля на трассах КЛ достаточно учитывать несколько первых гармоник ряда Фурье распределения поля. Расчет характеристик ЭМП и построение графического образа выполняется на персональном компьютере (ноутбуке), который выполняет функции: цифровой фильтрации аналоговых сигналов и выделения значений фазовых соотношений; определения спектральных составляющих аналоговых сигналов двух каналов; определения спектральной плотности мощности сигналов; управления интерфейсом.

Полевые испытания исследовательского прототипа устройства, в котором реализована обработка спектральных характеристик поля по прикладным программам быстрого преобразования Фурье, показали, что у всех видов повреждений кабеля формируются специфические образы, изменяемые при движении вдоль трассы прокладки КЛ (рис. 3).

Рис. 3 – Конфигурации электромагнитного поля над местом повреждения КЛ при: а – высоком переходном сопротивлении места повреждения; б – малом переходном сопротивлении места повреждения.

Графическая информация, отображаемая на экране ноутбука оператора, позволяет однозначно определить место и классифицировать причину повреждения КЛ.

Литература

1. Положение ОАО «Россети» о единой технической политике в электросетевом комплексе. М.: ОАО «Россети», 2013. 196 с.
2. Сазыкин В.Г., Кудряков А.Г. Нетребко С.А. Теоретический и практический аспекты повышения надежности кабельных линий электропередачи // Коллективная монография: Актуальные вопросы технических наук: Теоретический и практический аспекты. – Уфа: Аэтерна, 2014. – С. 127–154.
3. Сазыкин В.Г., Кудряков А.Г. Проблемы изношенного электрооборудования в современной энергетике // Международный научно-исследовательский журнал, 2015. № 7. С. 89–91.
4. Привалов И.Н. Современные методы и технические средства для испытаний и диагностики силовых кабельных линий номинальным напряжением до 35 кВ включительно. – Санкт-Петербург: Петербургский энергетический институт повышения квалификации руководящих работников и специалистов, 2008. 94 с.
5. Андре Анго. Математика для электро- и радиоинженеров. – М.: Наука, 1967. 780 с.
6. Андреев В.С. Теория нелинейных электрических цепей. – М.: Связь, 1972. 326 с.
7. Андронов А.А, Витт А.А., Хайкин С.Э. Теория колебаний. – М.: ФМЛ, 1981. 568 с.
8. Дементьев В.С. Как определить место повреждения в силовом кабеле. М.: Энергия, 1980. 72 с.

References

1. Polozhenie OAO «Rosseti» o edinoj tehnicheskoj politike v jelektrosetevom komplekse. M.: OAO «Rosseti», 2013. 196 s.
2. Sazykin V.G., Kudrjakov A.G. Netrebko S.A. Teoreticheskij i prakticheskij aspekty povyshenija nadezhnosti kabel'nyh linij jelektroperedachi // Kollektivnaja monografija: Aktual'nye voprosy tehnicheskih nauk: Teoreticheskij i prakticheskij aspekty. – Ufa: Ajeterna, 2014. – S. 127–154.
3. Sazykin V.G., Kudrjakov A.G. Problemy iznoshennogo jelektrooborudovanija v sovremennoj jenergetike // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal, 2015. № 7. S. 89–91.
4. Privalov I.N. Sovremennye metody i tehnicheskie sredstva dlja ispytanij i diagnostiki silovyh kabel'nyh linij nominal'nym naprjazheniem do 35 kV vkljuchitel'no. – Sankt-Peterburg: Peterburgskij jenergeticheskij institut povyshenija kvalifikacii rukovodjashhih rabotnikov i specialistov, 2008. 94 s.
5. Andre Ango. Matematika dlja jelektro- i radioinzhenerov. – M.: Nauka, 1967. 780 s.
6. Andreev V.S. Teorija nelinejnyh jelektricheskih cepej. – M.: Svjaz', 1972. 326 s.
7. Andronov A.A, Vitt A.A., Hajkin S.Je. Teorija kolebanij. – M.: FML, 1981. 568 s.
8. Dement'ev V.S. Kak opredelit' mesto povrezhdenija v silovom kabele. M.: Jenergija, 1980. 72 s.