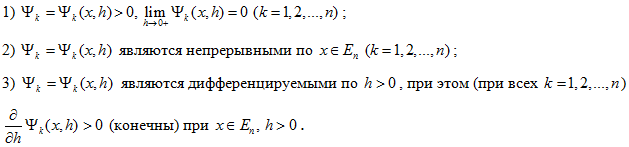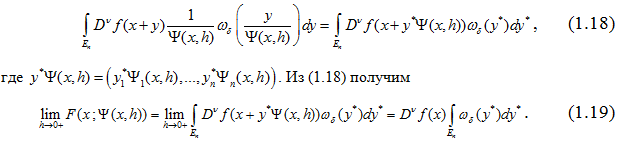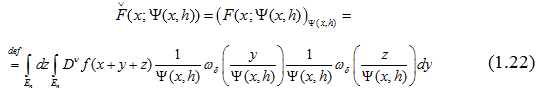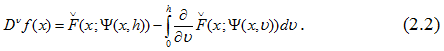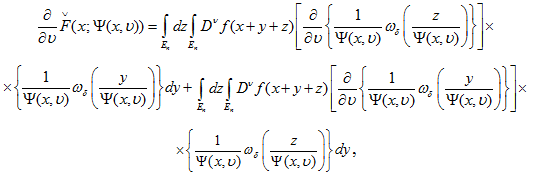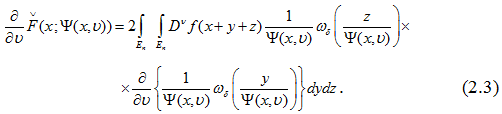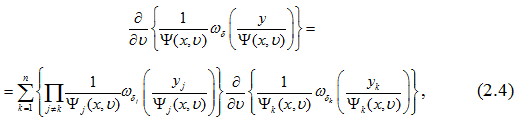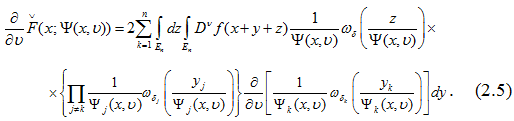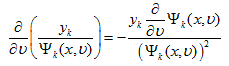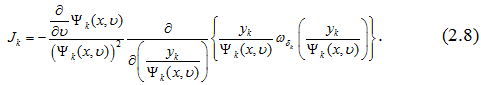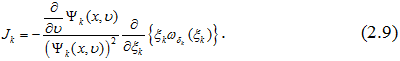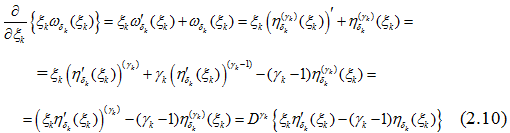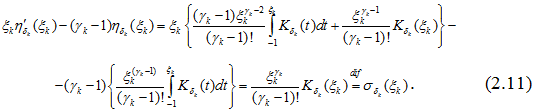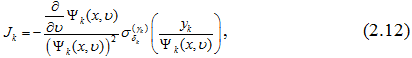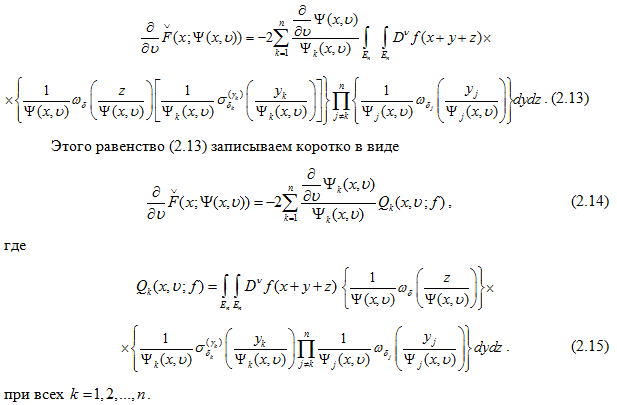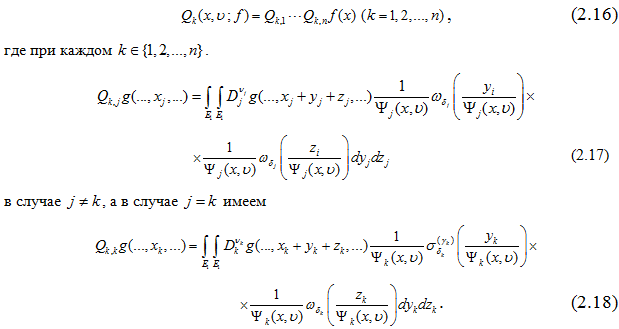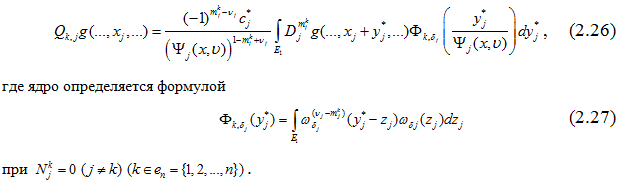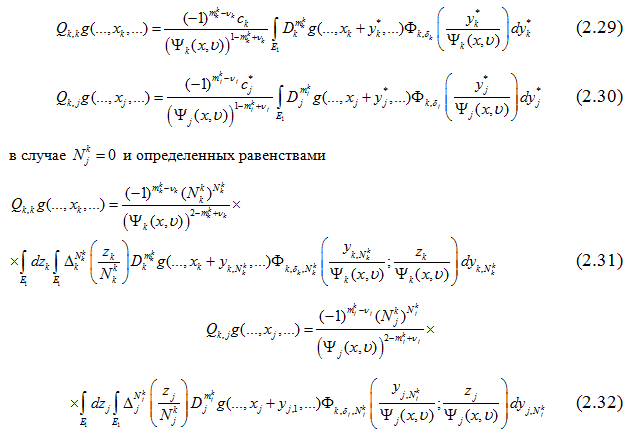SOME OPTIONS OF INTEGRATED REPRESENTATIONS DIFFERENTIABLE FUNCTIONS OF WEIGHT SPACES
Нейматов Назим Асадулла
Диссертант Институт Математики и Механики НАН Азербайджана
НЕКОТОРЫЕ ВАРИАНТЫ ИНТЕГРАЛЬНЫХ ПРЕДСТАВЛЕНИЙ ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЙ ВЕСОВЫХ ПРОСТРАНСТВ
Аннотация
В работе построены некоторые функциональные пространства дифференцируемых функций многих переменных и построенных весовых пространств.
Ключевые слова: пространства, вес, вектор, полурога, полунорма.
Neymatov Nazim Asadulla
Author of dissertation Institute of Mathematics and Mechanics of NAN of Azerbaijan
SOME OPTIONS OF INTEGRATED REPRESENTATIONS DIFFERENTIABLE FUNCTIONS OF WEIGHT SPACES
Abstract
In work some functional spaces of differentiable functions of many variables and the constructed weight spaces are constructed.
Key words: Spaces, everything, a vector, semihorns, seminorm.
1. Построение усредняющей функции.Предполагаем, что функция ![]() достаточно гладкой в точках x∈G⊂En.
достаточно гладкой в точках x∈G⊂En.
Займемся построением усредняющей функции. Положим, что
является достаточно гладкой, финитной в E1, такой что носитель этой функции подчиняется условиям:
при этом положим, что
Обозначим через
где γ>0-является достаточно большим целым числом.
Теперь положим, что вектор δ=(δ1,…, δn) с координатами
Пусть
при этом (см. (1.4))
Пусть (см. (7), (8))
при t=(t1,…, tn).
Положим, что вектор-функция
с координатами – функциями
удовлетворяет условия:
Теперь обозначим через
при x,yϵEn, где
Пусть вектор
является вектором с целыми неотрицательными координатами (т.е. ![]() -целые).
-целые).
Приведено усреднение достаточно гладкой функции
с помощью ядра (1.12), равенством:
Заметим, что после замены переменных
имеем
Легко убедиться (см. (1.3)) в том, что
Из двух равенств (1.19), (1.20) следует, что
в некоторой точке xϵEn.
Теперь приведем вторичные усреднения функций ![]() , равенством
, равенством
Аналогично доказательству равенства (1.21) можно убедиться в том, что
2. Основное тожество.Из основной формулы интегрального исчисления
при h0→0+ следует основное тождество
Равенство (2.2) является основой при доказательстве интегрального представления функции f=f(x).
2.1. Заметим, что (после простых рассуждений) выражение
из равенства (2.2) записывается (см.1.22) в виде
откуда следует, что в последнем равенстве, в правой части стоит сумма двух одинаковых интегральных выражений, т.е.
Если учесть равенства
тогда имеем
В этом равенстве (2.5), из интегральных операторов, стоящих в правой части, выделяем под интегральный множитель
который перепишем в виде:
следовательно, имея в виду, что
получим
Теперь обозначим через ![]() , тогда равенство (2.8) переобозначается в виде
, тогда равенство (2.8) переобозначается в виде
Второй множитель, в правой части равенства (2.9), преобразуется следующим образом (см. (1.7))
Выражение в фигурных скобках, правой части равенства (2.10), имеет следующий вид (см. (1.8)):
Из двух равенств (2.9) и (2.11) имеет:
где функция ![]() определена равенством (2.11) является достаточно гладкой и финитной функцей в E1. В равенстве (2.5), учитывая (2.12), получим
определена равенством (2.11) является достаточно гладкой и финитной функцей в E1. В равенстве (2.5), учитывая (2.12), получим
Заметим, что интегральные операторы Qk (x,v;f) (k=1,2,…,n) из (2.15) представляются в виде произведений интегральных операторов, точнее представляются в виде последовательного применения «одномерных интегральных операторов» в виде:
2.2. Преобразования интегральных операторов Qk,j(x,v;f) (j≠k) и Qk,k(x,v;f) при всех k=1,2,…,n (см.(2.17) и (2.18)). Напомним, что при каждом k ϵ {1,2,…,n}
преобразуем в отдельности.
- Преобразование интегрального оператора Qk,kg.
- Преобразования интегральных операторов Qk,jg(j≠k).
- В условиях
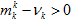 , производя замену переменных
, производя замену переменных  , после соответствующих преобразований.
, после соответствующих преобразований. - При фиксированном k ϵ en={1,2,…,n} в случае j≠k, в предположении
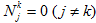 в условиях
в условиях 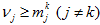 , после замены переменных
, после замены переменных 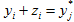 (j≠k), имеем
(j≠k), имеем
5. Преобразование интегрального оператора при ![]() .
.
- Преобразование интегрального выражения, при
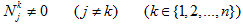 , ведется аналогичными рассуждениями, приведенными при преобразовании интегрального оператора при
, ведется аналогичными рассуждениями, приведенными при преобразовании интегрального оператора при 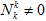 .
. - Теперь окончательную форму интегральных операторов
получаем применением (последовательно) интегральных операторов Qk,jg(…,x,…), определенных первов равенствами
в случае ![]() . После соответствующих вычислений имеем окончательную форму интегральных операторов в виде:
. После соответствующих вычислений имеем окончательную форму интегральных операторов в виде:
Литература
- С.Л.Соболев. Некоторые применения функционального анализа в математической физике. Из-во ЛГУ, 1950 г.
- О.В.Бесов, В.П.Ильин, С.М.Никольский. Интегральные представления функций и теоремы вложения. Москва, из-во «Наука», 1975 г.
- С.М.Никольский. Приближение функций многих переменных и теоремы вложения. Москва, из-во «Наука», 1977 г.
- Ф.Г.Максудов, А.Дж.Джабраилов. Метод интегральных представлений в теорий пространств. Баку, из-во, «Элм», 2000 г.
- А.Дж.Джабраилов. Теория пространств дифференцируемых функций. Труды ИММАН Азерб.Республики (вып.XII), Баку, «Элм», 2005 г.
- Т.И.Аманов. Пространства дифференцируемых функций с доминирующей смещенной производной. Алма-Ата, «Наука», 1976 г.
References
- S.L.Sobolev. Nekotorye primenenija funkcional'nogo analiza v matematicheskoj fizike. Iz-vo LGU, 1950 g.
- O.V.Besov, V.P.Il'in, S.M.Nikol'skij. Integral'nye predstavlenija funkcij i teoremy vlozhenija. Moskva, iz-vo «Nauka», 1975 g.
- S.M.Nikol'skij. Priblizhenie funkcij mnogih peremennyh i teoremy vlozhenija. Moskva, iz-vo «Nauka», 1977 g.
- F.G.Maksudov, A.Dzh.Dzhabrailov. Metod integral'nyh predstavlenij v teorij prostranstv. Baku, iz-vo, «Jelm», 2000 g.
- A.Dzh.Dzhabrailov. Teorija prostranstv differenciruemyh funkcij. Trudy IMMAN Azerb.Respubliki (vyp.XII), Baku, «Jelm», 2005 g.
- T.I.Amanov. Prostranstva differenciruemyh funkcij s dominirujushhej smeshhennoj proizvodnoj. Alma-Ata, «Nauka», 1976 g.