ПРОГНОЗИРОВАНИЕ ПОТРЕБЛЕНИЯ ЭНЕРГОРЕСУРСОВ НА ОСНОВЕ МОДЕЛИ ХОЛЬТА-УИНТЕРСА

Кузнецова И.Ю.

Ассистент проблемно-ориентированной кафедры «Математическое обеспечение суперкомпьютеров», Южный федеральный университет

ПРОГНОЗИРОВАНИЕ ПОТРЕБЛЕНИЯ ЭНЕРГОРЕСУРСОВ НА ОСНОВЕ МОДЕЛИ ХОЛЬТА-УИНТЕРСА

Работа выполнена при частичной поддержке РФФИ (проект: № 13-01-00530)

Аннотация

В данной статье описана одна из наиболее популярных адаптивных моделей прогнозирования — модель Хольта-Уинтерса. В статье отмечены достоинства и недостатки данной модели. Приведены результаты прогнозирования энергопотребления на основе метода Хольта-Уинтерса, и зависимость точности прогноза от выбора параметров модели.

Ключевые слова: адаптивные методы, модель Хольта-Уинтерса, прогнозирование, энергопотребление.

Kuznetsova I.Y.

Assistant, Southern Federal University

PREDICTION OF ENERGY CONSUMPTION BASED ON HOLT-WINTERS MODEL

Abstract

In the article described one of the most popular adaptive models — Holt-Winters model. It includes a review of strengths and weaknesses of this model, the results of forecasting energy consumption based on the Holt-Winters model, and how forecasting error depends on the choice of the model parameters.

Keywords: adaptive methods, Holt-Winters model, forecasting, energy consumption.

В настоящее время существует множество моделей прогнозирования и с каждым днем их становится все больше. По этой причине выбор той или иной модели при прогнозировании некоего процесса зависит от мнения эксперта или сравнения результатов прогнозирования различных моделей.

В настоящее время наиболее часто встречающимися моделями являются модели регрессии. Регрессионные модели широко распространены на практике, так как позволяют учесть влияние нескольких факторов (независимых переменных)  на исследуемый процесс (зависимую переменную) . В общем виде модели множественной регрессии можно записать как

              (1)

где  — зависимая переменная, ,  — независимые переменные, m — количество независимых переменных,  — коэффициенты модели.

Достоинствами регрессионных моделей является простота, гибкость и наличие общего подхода к анализу модели и прогнозированию [6]. Недостатками данных моделей является сложность определения вида функциональной зависимости и выбора независимых переменных, а также отсутствие возможности адаптации к новым данным.

Кроме регрессионных моделей, очень популярны модели авторегрессии ( и многие другие). Но при всей своей простоте и разнообразии, авторегрессионные модели также обладают рядом недостатков, главным из которых является необходимость определения большого числа параметров, при этом единого алгоритма определения параметров модели в настоящий момент не существует.

В настоящее время одним из наиболее перспективных направлений прогнозирования являются адаптивные методы, позволяющие учитывать разную степень влияния исторических данных. Модели авторегрессии в этом аспекте сходны с адаптивными моделями, но при классификации их выделяют в отдельную группу.

Основным достоинством адаптивных моделей является их способность подстраиваться под поступающую информацию, таким образом, нет необходимости начинать расчеты заново, как, например, в регрессионных моделях.

Одной из наиболее популярных является модель Хольта-Уинтерса, которая имеет вид:

        (2)

где l — размер периода прогнозирования, m — количество сезонов в полном цикле,  — сглаженный уровень без учета сезонности

      (3)  — сглаженный тренд          (4)  — сглаженная сезонность            (5)  — параметры модели.

На основании данных по потреблению электроэнергии за 2010-2011 гг. общежитиями студенческого городка ЮФУ в г. Таганроге и модели Хольта Уинтерса (2-5) были получены следующие прогнозные значения потребления электроэнергии на 2011-2013 года, которые были сравнены с данными по потреблению электроэнергии за тот же период. Результаты были получены при различных значениях параметров модели:

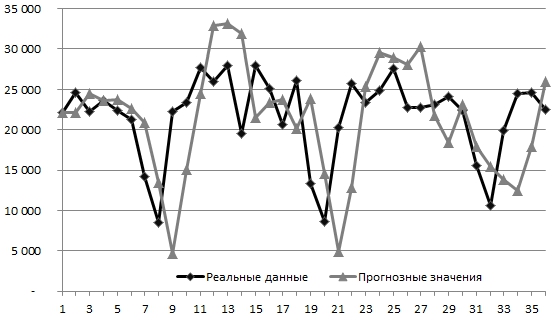
Рис. 1 - График потребления электроэнергии на 2011-2013 гг. при 

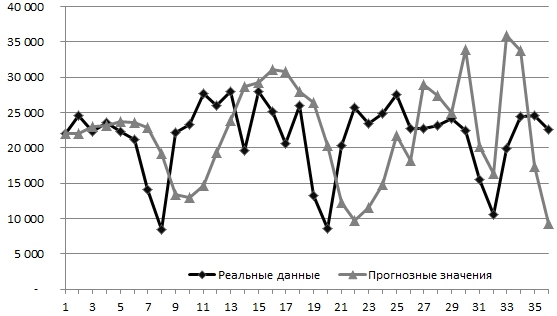
Рис. 2 - График потребления электроэнергии на 2011-2013 гг. при 

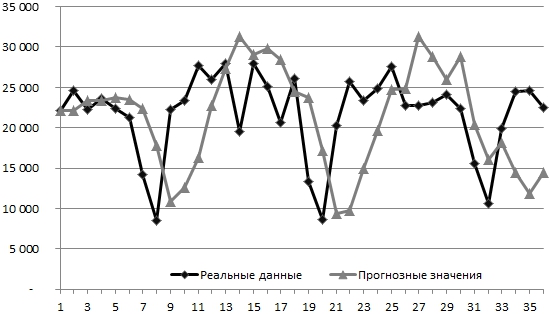
Рис. 3 - График потребления электроэнергии на 2011-2013 гг. при 

Определение качества модели [1] проводилось на основании определения средней относительной ошибки прогноза:

,

где  — модельная погрешность в i-ый момент времени,  — фактическое значение потребления электроэнергии в i-ый момент времени, n — длительность периода прогнозирования в месяцах.

Полученные результаты представлены в таблице 1.

 

Таблица 1

На основании полученных результатов можно говорить о том, что модель Хольта-Уинтерса может быть применена к прогнозированию потребления электроэнергии, но только при условии подбора параметров модели. К сожалению, алгоритма определения параметров модели нет, к тому же модель Хольта-Уинтерса не учитывает случайные колебания, как, например, модель на основе стохастических дифференциальных уравнений [2,3].

Литература

1. Кузнецова И.Ю. Критерии оценки качества прогноза // Наука и образование в XXI веке: сборник научных трудов по материалам Международной научно-практической конференции 30 сентября 2013 г.: М-во обр. и науки РФ. Тамбов: Изд-во ТРОО «Бизнес-Наука-Общество» — 2013. — Часть 28 — С. 85-86.
2. Кузнецова И.Ю. Математическая модель прогнозирования энергопотребления // Известия Южного федерального университета. Технические науки. — 2013. — №4 — С. 121-125.
3. Кузнецова И.Ю. Математическая модель энергопотребления применительно к ВУЗу // Известия Южного федерального университета. Технические науки. — — Т.121 №8 — С. 183-186.
4. Кузнецова И.Ю. Численное решение стохастических дифференциальных уравнений в финансах // Известия Южного федерального университета. Технические науки. — 2013. — №4 — С. 175-184.
5. Кузнецова И.Ю. Численное решение стохастического дифференциального уравнения методом Эйлера-Маруямы // Международный научно-исследовательский журнал. № 11-1 (18). С. 8-11.
6. Draper N., Smith H. Applied regression analysis. New York: Wiley, In press, 1981. 693 p.