ОБОСНОВАНИЕ ПАРАМЕТРОВ ГОРНЫХ ПОРОД (НЕОДНОРОДНЫХ СРЕД) ПРИ МОДЕЛИРОВАНИИ
Катанов Ю.Е.1, Григорьев Н.В.2
1Преподаватель кафедры моделирования и управления процессами нефтегазодобычи, Тюменского Государственного Нефтегазового Университета, магистр, Факультет информационные системы и технологии; 2Специалист, Факультет разработки и эксплуатации нефтяных и газовых месторождений, Тюменский Государственный Нефтегазовый университет
ОБОСНОВАНИЕ ПАРАМЕТРОВ ГОРНЫХ ПОРОД (НЕОДНОРОДНЫХ СРЕД) ПРИ МОДЕЛИРОВАНИИ
Аннотация
В статье рассмотрена начальная аналитическая схема для оценок статистических объемов слабых локальных областей и зон разрушения горных пород.
Ключевые слова: динамическая модель, физическая модель, дисперсионный анализ, горная порода, зона разрушения.
Katanov Y.E.1, Grigoriev N.V.2
1Assistant-teacher, Department of simulation and process control of oil and gas production, Tyumen State Oil and gas University, Master, the Faculty of information systems and technologies; 2Specialist, Faculty of development and exploitation of oil and gas fields, Tyumen State Oil and gas University
SUBSTANTIATION OF THE PARAMETERS OF ROCKS (HETEROGENEITY ENVIRONMENTS) WHEN MODELING
Abstract
The article considers the initial analytical scheme for estimation of statistical quantities weak local areas and areas of rock fracture.
Keywords: the dynamic model, physical model, analysis of variance, rock, the zone of destruction.
При разработке статистических теорий прочности пространственных твердых тел используется концепция наислабейшего звена, в соответствии с которой разрушение горной породы происходит по наиболее дефектному звену [2,3,4].
Статистическая динамическая модель горной породы может быть представлена как система усложняющихся моделей [1]:
- физическая модель первого уровня - горная порода описывается как совокупность распределенных по объему дефектов (без учета физико- химических факторов), при этом деформационно-пространственная стабильность породы сохраняется до тех пор, пока в породе не возникают опасные дефекты;
- физическая модель горной породы второго уровня характеризует состояние породы в период активизации процессов разрушения горной породы, когда имеет место значительное усиление физико-химического взаимодействия;
- динамические факторы описывают тенденции развития дефектной структуры горных породах в результате комплекса эксплуатационных воздействий (обводнения, волновых и механических нагрузок, и др.).
Статистическая природа динамической модели горной породы состоит в том, что:
- в модели первого уровня принимается, что дефекты в объеме горной породе распределены случайным образом;
- в модели второго уровня принимается, что вероятность возникновения локальной области адсорбционного ослабления - случайное событие.
В рамках модели первого уровня для вероятности сохранения деформационно-пространственной стабильности породы получено соотношение [1]:
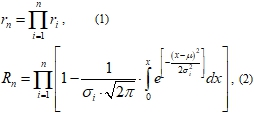
где pi - вероятность по i-му фактору возникновения слабейшего звена,
![]() - дисперсия по i-му фактору,
- дисперсия по i-му фактору, ![]() - параметр отсечения по i-му фактору.
- параметр отсечения по i-му фактору.
Следует отметить, что выражения (1-2) получены при допущении, что факторы независимы друг от друга.
К факторам ослабления породы могут быть отнесены:
- характеристики породы - прочность, пористость, параметры пространственных связей и др.;
- показатели, характеризующие степень внешнего воздействия на породу - физико-технические воздействия, гидродинамические нагрузки и др.
Для примера рассмотрен один из физико-технических факторов - прочность породы на сжатие ![]() , как нормально распределенную величину (рис. 1).
, как нормально распределенную величину (рис. 1).
При этом меняется от нуля до некоторого значения, средневзвешенная прочность сжатие составляет ![]() .
.
Существует некоторая минимальная величина прочности ![]() , ниже которой происходит разрушение породы, испытывающей комплекс нагрузок.
, ниже которой происходит разрушение породы, испытывающей комплекс нагрузок.
В диапазоне от нуля до ![]() лежит сектор слабых локальных областей породы, причем
лежит сектор слабых локальных областей породы, причем ![]() - точка отсечения по прочности на сжатие.
- точка отсечения по прочности на сжатие.
Аналогичным образом определяются параметры отсечения по другим характеристикам пород.
Величина дисперсии распределения некоторого параметра породы имеет принципиальное значение при определении размера зон устойчивости и разрушения породы.
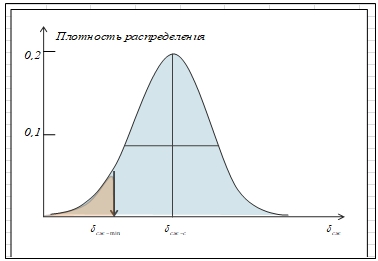
Рис. 1 - Сектор слабых локальных областей породы (темный треугольник) на кривой распределения прочности на сжатие
На рис. 2 показаны узко- и широко дисперсное распределения при одинаковых математических ожиданиях распределений, а рис. 3 - сектора слабых локальных областей для распределения, приведенного на рис. 2.
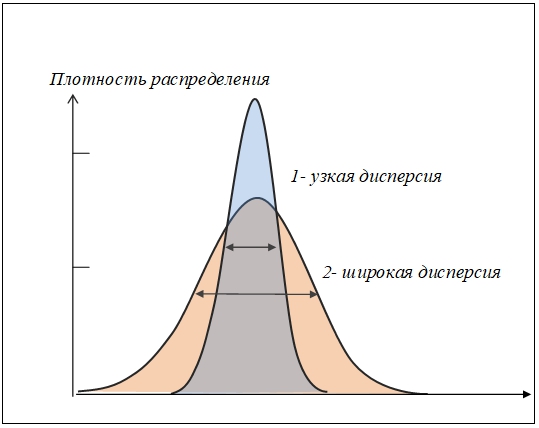
Рис. 2 - Широко- дисперсное и узко- дисперсное распределения
При высокой дисперсии (кривая 1, рис. 3) размер зоны разрушения много выше, чем при малой дисперсии (кривая 2, рис. 3) [1].
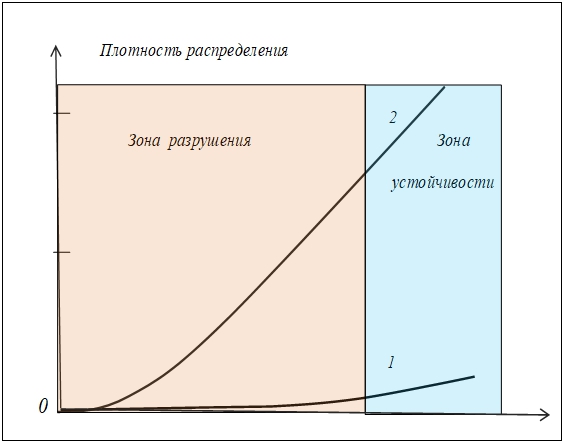
Рис. 3 - Зоны разрушения и устойчивости при разных дисперсиях распределения
Для аналитических оценок статистических объемов слабых локальных областей и зон разрушения был разработан новый подход и методы оценивания характеристик горных пород как неоднородных сред - метод статистических смещенных оценок горных пород, в основе которого лежит представление о механизмах процессов, протекающих в породах в условиях сложного воздействия [1].
В случае если в расчет принимаются средние параметры пород, то возможна систематическая ошибка, вызванная тем, что горная порода - высоко неоднородная среда, и для корректного нахождения ее параметров необходимы методы, принципы которых описаны в работе [1].
Литература
- Катанов Ю.Е. Материалы диссертационной работы «Физико-математическое моделирование в методологии технологических измерений в нефтедобыче» на соискание ученой степени кандидата ф-м. наук. Тюмень, 2014.
- Вознесенский Е.А. Динамическая неустойчивость грунтов / Е.А. Вознесенский. -М.: Эдиториал УРСС, 1999, - 263 С.
- Ребиндер П.А. Избранные труды. Поверхностные явления в дисперсных системах. Коллоидная химия. M.: Наука, 1978, - 196 С.
- Клабуков Б. Н. Неоднородность геологической среды по данным геофизических исследований. Геология и полезные ископаемые Карелии. Выпуск 12. Петрозаводск, - 2009.
