ЛАБОРАТОРНО-ПРАКТИЧЕСКИЕ РАБОТЫ КАК СРЕДСТВО РАЗВИТИЯ ИССЛЕДОВАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИ УЧАЩИХСЯ СРЕДНЕЙ ШКОЛЫ ПРИ ОБУЧЕНИИ МАТЕМАТИКЕ

Аммосова Н.В.¹, Коваленко Б.Б.²

¹Профессор, доктор педагогических наук, ²доцент, кандидат физико-математических наук, Астраханский государственный университет

ЛАБОРАТОРНО-ПРАКТИЧЕСКИЕ РАБОТЫ КАК СРЕДСТВО РАЗВИТИЯ ИССЛЕДОВАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИ УЧАЩИХСЯ СРЕДНЕЙ ШКОЛЫ ПРИ ОБУЧЕНИИ МАТЕМАТИКЕ

Аннотация

Выдвигается точка зрения на выполнение лабораторно-практических работ учащимися при изучении математики как на средство развития исследовательской деятельности школьников, которое, к сожалению, используется недостаточно в практике работы учителей, а между тем, оно является одним из методических реализаций синергетического подхода в образовании.

Ключевые слова: лабораторно-практическая работа, учащиеся, математика.

Ammosov N. V.¹, Kovalenko B. B.²

¹Professor, doctor of pedagogical sciences, ²PhD in Physics and mathematics, assosiate professor, Astrakhan state university

LABORATORY WORKS AS THE DEVELOPMENT TOOL OF RESEARCH ACTIVITY OF PUPILS OF HIGH SCHOOL WHEN TRAINING IN MATHEMATICS

Abstract

The point of view on performance of laboratory works by pupils moves forward when studying mathematics as on a development tool of research activity of school students which, unfortunately, is used insufficiently in practice of work of teachers, and meanwhile, it is one of methodical realization of synergetic approach in education.

Keywords: laboratory- practical work, pupils, mathematics.

Одним из методических реализаций синергетических идей в образовании является выполнение учащимися лабораторно-практических работ при обучении в средней школе, в том числе, и на занятиях по математике, что практикуется довольно редко. Синергетическое знание становится методом, инструментом поисковой деятельности.

Кроме того, лабораторно-практические работы можно рассматривать и как средство развития исследовательской деятельности школьников. Синергетика выполняет эвристическую функцию в познании, то есть может помочь определить в исследовании следующий шаг.

Проводя самостоятельную работу с учащимися, учителя, чаще всего, рассматривают её как самоцель, не акцентируя свое внимание на том, способствует ли она активной мыслительной деятельности ученика или нет. Часто большое число самостоятельных работ направленно лишь на выполнение заданий по образцу, среди которых мало заданий исследовательского характера. Между тем, от становления самостоятельности зависит активность ученика, его ориентировка в окружающей действительности.

Один из недостатков в методике проведения самостоятельных работ состоит в однообразии их видов, используемых учителем. Абсолютное большинство самостоятельных работ на уроках математике приходится на закрепление изложенного учителем материала непосредственно после его изучения и на проверку знаний учащихся. Значительно меньшее число их используется при изучении нового материала.

По содержанию все работы должны иметь практическую направленность, способствовать выработке у учащихся практически важных умений и навыков, которые они могли бы использовать на уроках труда, при изучении других учебных предметов (черчения, географии, физики, химии), в быту, при продолжении общего или получении профессионального образования.

Хорошо, если предлагаемая учащимся лабораторно-практическая работа не является изолированной, а предполагает выходы в окружающий мир. Приведем пример.

Понятие винтовой линии не является обязательным в школьной программе, но поскольку оно имеет многочисленные приложения, то полезно познакомить с ним старшеклассников хотя бы в рамках факультатива, спецкурса или электива. Кроме того, оно является довольно абстрактным, если останавливаться лишь на его строго математическом содержании: винтовая линия трактуется как «материализованный» след винтового движения, а винтовое движение точки – как композиция (последовательное применение) ее вращения вокруг некоторой прямой, называемой осью вращения, и параллельного переноса вдоль этой оси на некоторый вектор. Однако никогда не следует пренебрегать возможностью использовать наглядность, задействуя образную составляющую мышления. С этой целью учащимся целесообразно предлагать задания, дающие возможность «материализовать» математическое понятие, например, реализуя технологию получения винтовой линии [1].

Лабораторно-практическая работа «Получение винтовой линии».

Для получения витка винтовой линии учащиеся изготавливают бумажный прямоугольный треугольник, один из катетов которого равен длине окружности основания имеющегося цилиндра (вычисляется по формуле  πD, где D –  диаметр основания), а другой – его высоте ВС.

Поскольку учащиеся приносят разные цилиндры по высоте и площади основания (приносятся разные и по материалу, из которого изготовлены цилиндры, цвету и другим параметрам, но это несущественные признаки для решаемой задачи), то у каждого из них получаются разные витки винтовой линии. Отрезок ВС называется шагом винтовой линии.

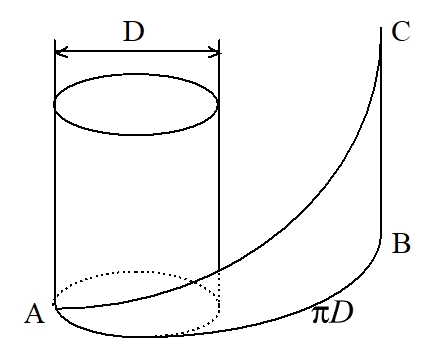
Рис.1 - Получение винтовой линии

Далее представляется естественным обсудить с учащимися практическую значимость полученных результатов. Оказывается, в зависимости от шага изготавливают винты с разной резьбой. Резьба с малым шагом применяется в шурупах для крепежных работ, а резьба с малым шагом используется там, где нет больших усилий. Учащиеся делают выводы о практической применимости разных резьб.

Винтовая линия получается как последовательное продолжение одного витка другим. Раскрывается и содержание понятия винтового движения как композиции (результату последовательного применения) двух движений.

Полученные знания применяются учащимися при решении задач с практическим содержанием.

Задача. Охарактеризовать винтовое движение в структуре киновари HgS (Рис.2):

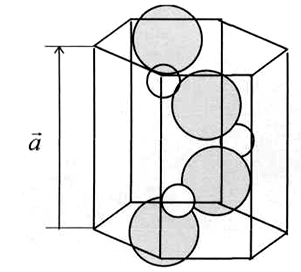
Рис.2 - Структура киновари

Учащиеся выделяют шаг и другие характеристики молекулы киновари, а также приводят примеры винтовой линии (например, винтовая лестница), винтового движения в окружающем мире (например, движение карандаша при заточке его школьной точилкой, ввертывание или вывертывание шурупа или винта).

Таким образом, исследовательские лабораторно-практические работы направлены на практический поиск новых свойств, которые затем будут логически обоснованы.

Можно не обязывать школьников приносить готовые цилиндры, а изготовить их на уроке или дома (домашняя лабораторно-практическая работа), то есть объявить лабораторно-практическую работу «Изготовление модели цилиндра».

Работами подобного типа являются лабораторно-практические работы «Построить развертку и изготовить по ней  модель куба с длиной стороны 4 см», «Изготовить пирамиду, в основании которой лежит правильный треугольник, а боковое ребро перпендикулярно плоскости основания».

Преимущество лабораторно-практического метода состоит в том, что школьник сам становится участником эксперимента, выявляет закономерности и свойства геометрического тела и в результате получает его реальную модель.

Модель геометрического тела, выполненная руками самого учащегося, оставляет в его памяти яркое и сильное по эмоциональному состоянию впечатление. Кроме того, организация практической деятельности школьника стимулирует развитие любознательности как начальной ступени познавательного интереса, без которого не может быть творческой личности.

У ряда учащихся интерес к занятиям по математике и к учению в целом развивается через практическую деятельность. Учителю необходимо использовать этот путь вовлечения учащихся в творческую деятельность, способствующий развитию таких исследовательских качеств личности, как предвидение и прогнозирование.

Практические работы, помимо решения своей специальной задачи — усиления практической направленности обучения, не только теснейшим образом связаны с изучаемым материалом, но и способствуют прочному, неформальному его усвоению, достижению основных образовательных, воспитательных и развивающих целей обучения математике. И конечно, тематика лабораторно-практических работ весьма обширна и не ограничивается лишь некоторыми геометрическими разделами, которые использовались в этой статье.

Наша многолетняя практика показывает, что организация обучения школьников на основе изложенных положений помогает сделать учение увлекательным, развивающим творчество и исследовательские качества учащихся.

 

Литература

1. Аммосова Н.В. Развитие творческой личности школьника при обучении математике: Учебное пособие. – Астрахань: Изд-во АИПКП, 2006. – 224 с.