Численное решение одной задачи распределённой управляемости в среде Mathcad
Численное решение одной задачи распределённой управляемости в среде Mathcad
Аннотация
В статье предлагается алгоритм численного решения задачи распределённой управляемости процессом остывания тонкого однородного стержня с теплоизолированной боковой поверхностью.
Для моделирования и визуализации процесса использована система компьютерной алгебры Mathcad 15. Исследованы возможности и ограничения, возникающие при моделировании решения задачи в этой системе. При этом моделирование осуществлено двумя способами: с использованием чисто встроенных средств среды, предназначенных для решения уравнений в частных производных, а также с использованием встроенных средств программирования (таких, как операторы циклов, условные переходы). В последнем случае предлагаемые численные алгоритмы легко переносятся на любой «чистый» язык программирования, что может быть оправдано желанием получить более высокую скорость и точность вычислений.
Ключевой особенностью данной работы являются, помимо получения аналитического решения задачи, практические оценки найденных функций и параметров, а также проведение численного моделирования.
1. Введение
В теории динамических систем задачами управляемости принято называть задачи приведения динамической системы к заданному состоянию при наличии некоторого управляющего воздействия
, , . Управляющим воздействием может являться граничный режим, режим, распределённый по всей рассматриваемой области, либо по её части и т.д. При этом важным является, помимо обоснования существования решения с получением явных формул, нахождение эффективных оценок всех параметров, а также организация эффективных вычислений.Статья
является обзорной и содержит результаты многих авторов, касающиеся граничной управляемости мембран и пластин с помощью различных краевых условий. Одной из пионерских работ в данной области является также монография , в которой рассматриваются постановки и решения задач как граничной, так и распределённой управляемости, как для параболических, так и для гиперболических уравнений и систем. Рассматриваемые задачи моделируют такие процессы, как: оптимальный нагрев массивных тел, нагрев металлов в методической печи, охлаждение прокатных валков, индукционный нагрев, сушка и обжиг сыпучих материалов, дистилляция и т.д. Для указанных процессов характерно то, что обработка материала происходит во время их пространственного движения через зоны обработки. При этом на материал оказывается именно распределённое воздействие, причём не только во времени, но и в пространстве. Отметим, что в для решения задач управляемости впервые был эффективно применён метод моментов.Из более современных источников следует отметить монографию
, в которой изложение методов иллюстрируется большим количеством актуальных задач управления для различных механических и электромеханических систем: манипуляционных роботов, маятниковых систем, электроприводов, многомассовых систем с сухим трением, активных гасителей колебаний и т.д. Основным рабочим методом здесь является метод декомпозиции управления. В , рассматриваются задачи управляемости системами с интегральной «памятью», исследование которых получило наибольшее распространение в последние 15-20 лет. Такими моделями описываются задачи механики гетерогенных сред, теории вязкоупругости, теплофизики и кинетической теории газов. Основным инструментом исследования здесь выступает метод Фурье и его аналоги. Применению метода Фурье к решению одной задачи управляемости посвящена и настоящая статья.Мы будем рассматривать задачу об остывании тонкого однородного стержня с теплоизолированной боковой поверхностью, считая управляющим воздействием плотность распределения источников тепла по всему стержню. При этом нужно учитывать ограниченность имеющихся ресурсов, потому функция управления не должна принимать сколь угодно больших значений. В качестве исходных данных примем известное ненулевое начальное распределение температуры по всей длине стержня, а также будем считать, что температура концов стержня поддерживается равной нулю.
Хорошо известно, что процесс теплопроводности (диффузии) при отсутствии источников диссипативен и нетрудно доказать, что охлаждение стержня до нулевой температуры при описанных выше условиях происходит всегда, но за бесконечное время (см.
).Особенность рассматриваемой задачи состоит в том, что требуется охладить стержень до нулевой температуры за конечное (необязательно минимальное) время. Ясно, что в такой постановке единственности решения задачи ожидать не следует.
Основной целью настоящей работы является простое обоснование разрешимости рассматриваемой задачи с использованием метода разделения переменных, не совпадающее со встречающимися в более ранних исследованиях. При этом должны быть получены явные эффективные оценки управляющего воздействия и времени этого воздействия. Оценка считается явной, если все присутствующие в ней константы выражаются явным образом. Оценка считается эффективной, если она обеспечивает эффективный вычислительный процесс в следующем смысле: в пределах заданной точности, после замены бесконечной суммы на конечную, в последней должно оставаться как можно меньше слагаемых. Кроме того, по возможности необходимо избежать численного интегрирования быстро осциллирующих функций. Результаты теоретических выкладок должны быть проиллюстрированы на модельном примере.
2. Постановка задачи и аналитические результаты
Пусть -- классическое решение в цилиндре
следующей задачи:
Здесь -- ненулевая ограниченная измеримая функция, для которой в
имеет место оценка
, константа
задана. Функция
, характеризующая плотность тепловых источников, является неизвестным управляющим воздействием. Требуется подобрать
таким образом, чтобы температура
при всех
, где
-- фиксированная постоянная (которую также требуется определить). Начальную температуру
будем считать ненулевой финитной бесконечно гладкой на интервале
функцией.
Хорошо известно
, что, при условиях, наложенных на функцииПрименяя метод разделения переменных
, получим решение задачи в видеЗдесь ,
.
Подберём функцию так, чтобы
при всех
и всех
, тогда получим, что
при всех
.
Будем искать непрерывные коэффициенты в виде
, тогда придём к равенству
Интегрируя, находим
.
Таким образом в качестве искомого управления можно взять . Из проводимых далее оценок следует, во-первых, что указанная функция непрерывна (как сумма равномерно сходящегося ряда), а, во-вторых, что написанный ряд действительно является рядом Фурье
Осталось выбрать такое , чтобы выполнялась оценка
. Очевидно, что оценки достаточно проводить только для случая
. Тогда, учитывая, что
при всех
, получим:
Здесь (ограниченность коэффициентов Фурье легко следует из ограниченности функции
) и использована сумма ряда обратных квадратов. Таким образом,
При практических вычислениях значений функции требуется заменить бесконечную сумму конечной, содержащей
слагаемых. Погрешность такой замены, очевидно, оценивается величиной
Легко видеть, что при выполняется неравенство
: при
неравенство проверяется непосредственно, после чего остаётся заметить, что функция
строго возрастает. Кроме того, заметим, что функция
строго убывает при
. Тогда, считая, что
из (5) получаем оценки:
где -- интеграл ошибок.
Отметим, что при численной реализации достаточно решить задачу только при . Если окажется, что
, то, полагая
при всех
, в силу теоремы единственности
3. Численное моделирование с использованием вычислительного блока Given/Pdesolve
Выполним численное моделирование в среде Mathcad решения задачи (1)-(3) на прямоугольнике с учётом построенной функции
и полученных оценок. Будем использовать встроенный вычислительный блок Given/Pdesolve
Использование вычислительного блока интуитивно понятно и приведено в листинге на рис. 1.
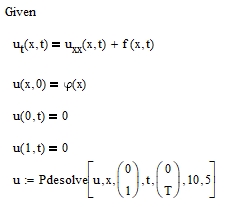
Рисунок 1 - Листинг вычислительного блока Given/Pdesolve
Результатом работы функции является интерполированная зависимость , что увеличивает общее время вычислений, однако позволяет сразу получать значения искомой функции в любой точке рассматриваемого прямоугольника.
Для начала вычислений необходимо определить момент , а также функцию
, для задания которой необходимо вычислить значение
. Примем
. Поскольку
, то из оценки (4) получаем, что
. Примем
. Заметим, что данный интеграл легко вычисляется встроенными средствами Mathcad, либо, при переводе вычислений на «настоящий» язык программирования, одним из стандартных вычислительных методов
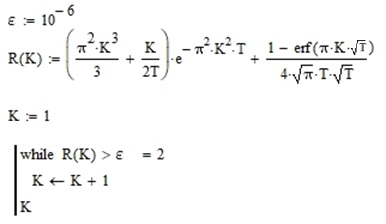
Рисунок 2 - Листинг нахождения K
В таблице 1 приведены результаты работы вычислительного блока при различных соотношениях количеств шагов по координате () и времени (
). Норма равномерная.
Таблица 1 - Результаты работы модуля Given/Pdesolve
M | 5 | 10 | 100 | 100 | - |
N | 5 | 5 | 5 | 100 | - |
||u(x,T)|| | 1,893х10-5 | 8,614х10-7 | 5,979х10-8 | 5,979х10-8 | 8,614х10-7 |
Очевидными достоинствами использования вычислительного блока являются получение интерполированных значений решения задачи, а также достижение приемлемой точности уже при небольшом количестве шагов дискретизации. Однако с увеличением числа шагов дискретизации скорость вычислений заметно снижается, а попытка рассчитать задачу при приводит к ошибке нехватки памяти. Кроме того, отсутствует наглядность вычислений, вследствие чего невозможно перевести вычисления на стандартные языки программирования.
В следующем разделе будут приведены варианты явных вычислений на основе построения разностных схем.
4. Численное моделирование на основе разностных схем
Введём в прямоугольнике сетку
,
,
,
,
,
,
,
-- шаги по координате и по времени соответственно. Явная разностная схема, аппроксимирующая задачу (1)-(3) имеет вид
Как известно
, данная разностная схема аппроксимирует дифференциальную задачу с порядкомПримем (максимально возможный временной шаг, обеспечивающий устойчивость разностной схемы), тогда основное соотношение (7) перепишется в виде:
Листинг программы в среде Mathcad, решающей по явной разностной схеме тот же самый модельный пример, что был рассмотрен в предыдущем разделе, приведен на рис. 3.
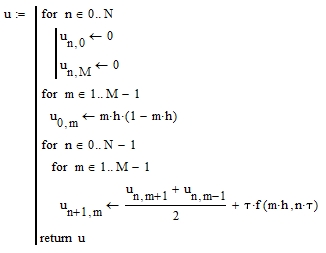
Рисунок 3 - Решение задачи при помощи явной разностной схемы
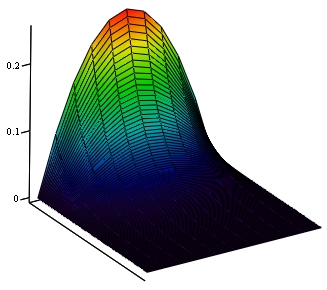
Рисунок 4 - Решение с использованием явной разностной схемы
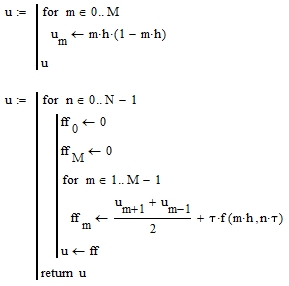
Рисунок 5 - Листинг оптимизированной программы, реализующей явную разностную схему

Рисунок 6 - «Максимальная» оптимизация расчётов по явной разностной схеме
Таблица 2 - Результаты решения задачи по явной разностной схеме
h | 0,1 | 0,01 | 0,001 | 0,0001 |
||u(x,T)|| | 7,831х10-5 | 8,01х10-7 | 8,011х10-9 | неприемлемо большое время вычислений |
Очевидным преимуществом явной разностной схемы является простота её реализации и скорость вычислений. Однако существенным недостатком является наличие условия устойчивости, заставляющего для достижения приемлемой точности решения рассчитывать большое количество временных слоёв сетки. Вычисления с шагом оптимизированные программы проводили около пяти минут (процессор Intel core i5 10500h, ОС – Windows 11). Не оптимизированная программа при этом выдала ошибку нехватки памяти (что обусловлено необходимостью хранения больших двумерных массивов во время работы программы). Время вычислений с шагом
оказалось неприемлемо большим даже для оптимизированных программ.
Чтобы избавиться от условия устойчивости, рассмотрим неявную шеститочечную разностную схему Кранка-Николсон
. Чтобы записать эту разностную схему, заменим уравнение (7) в системе (7)-(9) уравнениемРазностная схема (11), (8), (9) аппроксимирует дифференциальную задачу с порядком , что является её преимуществом перед простейшей неявной разностной схемой, а также является безусловно устойчивой. Решение этой разностной схемы сходится к решению дифференциальной задачи в равномерной норме со вторым порядком по времени и по координате. Вычисления по этой схеме организуются сложнее, чем по явной разностной схеме. Наиболее эффективным здесь является метод прогонки
На рис. 7 представлена реализация решения задачи при помощи неявной разностной схемы Кранка-Николсон (сразу в варианте без использования двумерных массивов). Алгоритм метода прогонки реализован в листинге на рис. 8.
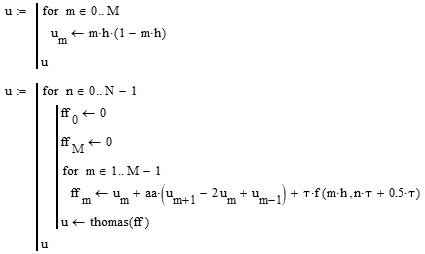
Рисунок 7 - Решение задачи по схеме Кранка-Николсон

Рисунок 8 - Метод прогонки (алгоритм Томаса)
Таблица 3 - Результаты решения задачи по схеме Кранка-Николсон
h | 0,1 | 0,1 | 0,01 | 0,001 | 0,0001 |
tau | 0,1 | 0,001 | 0,001 | 0,0001 | 0,00001 |
||u(x,T)|| | 1,176х10-3 | 1,199х10-5 | 1,947х10-7 | 1,947х10-9 | 1,712х10-11 |
5. Заключение
В статье показана принципиальная разрешимость одной задачи управляемости динамической системой. Проведены численные эксперименты, результаты которых согласуются с ожидаемыми, исходя из полученного аналитического решения. Преимуществом и новизной предложенного подхода является его простота, явные эффективные оценки управляющего воздействия и времени этого воздействия, не совпадающие с полученными в более ранних работах. Кроме того, впервые продемонстрированы возможности и ограничения системы Mathcad при решении подобных задач распределённой управляемости. При реализации метода сеток не использовались встроенные функции системы, что позволяет легко перевести все вычисления на любой современный язык программирования с целью ускорения и оптимизации.
Вместе с тем очевидна не единственность предложенного решения, которая связана с неоднозначностью определения коэффициентов . С практической точки зрения такой эффект не единственности является вполне естественным и приводит к вопросу поиска оптимального управления, переводящего рассматриваемую систему в заданное состояние. Здесь возможно два пути: минимизация некоторого функционала качества, либо минимизация промежутка времени
.
Также следует заметить, что рассматриваемую задачу можно считать обратной задачей математической физики
, когда требуется восстановить правую часть уравнения по известной дополнительной информации о решении. Поэтому представляет интерес рассмотреть решение этой же задачи с точки зрения методов решения обратных и некорректно поставленных задач математической физики.Наконец, ещё одним возможным направлением для дальнейшего численного моделирования является переход к рассмотрению двух- и трёхмерных (по пространству) моделей. Легко видеть, что предложенный в статье подход без труда распространяется и на этот случай.
