НАУЧНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА СТУДЕНТОВ ПЕРВОГО КУРСА

Супрун Л.И.¹, Супрун Е.Г.²

¹Кандидат технических наук, Доцент, ²Доцент, Сибирский федеральный университет

НАУЧНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА СТУДЕНТОВ ПЕРВОГО КУРСА

Аннотация

В статье приведён опыт организации научно-исследовательской работы со студентами 1 курса направления «Архитектура». На этом этапе перед студентами стоят задачи: приобретение дополнительных знаний, поиск и отбор материала по предложенной проблеме, анализ полученных сведений. Поэтому основным видом работы на 1 курсе является реферативная работа. Но в любую реферативную работу можно внести элементы исследования. Как это сделать, показано на приведённых в статье конкретных примерах.

Ключевые слова: дополнительные знания, анализ данных, научное исследование.

Suprun L.I.¹, Suprun Е.G.²

¹Candidate of Technical Sciences, Assistant Professor, ²Assistant Professor, Siberian Federal University

FRESH-YEAR STUDENTS RESEARCH WORK

Abstract

There is an experience of fresh year architect students, research work organization in the article. On this stage there are the following tasks for students: obtaining the optional knowledge, searching and selecting the suggested problem material, analyzing the found information. That is why the main work for fresh year students is abstracts work. But one can introduce elements of research. How to do it is shown by the given in the article examples.

Key words: optional knowledge, analyzing the data, scientific research.

Любая научно-исследовательская работа начинается с изучения состояния выбранной проблемы. Это и поиск литературы, и проработка размещённого в ней материала, и соответствующие выводы. На первом курсе студент ещё не обладает достаточными знаниями, чтобы проводить глобальные исследования. Поэтому первые навыки исследования первокурсник получает при выполнении реферативной работы. Но в реферативную работу можно включить и элементы исследования. Хотим поделиться опытом такой работы со студентами 1 курса направления «Архитектура». Дисциплина - начертательная геометрия.

Как правило, это происходит во втором семестре, когда студенты уже обладают некоторым багажом знаний и могут давать оценку различным ситуациям.

Пример 1. Студенты изучили основной курс начертательной геометрии и тени в ортогональных проекциях. Ставится задача: на конкретном примере показать связь между позиционными задачами и теорией теней [1].

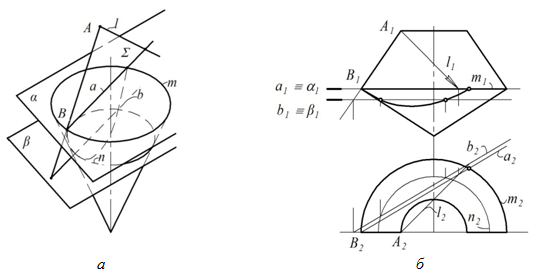
Задание. Имеется полуконическая ниша с открытым верхом и козырьком в форме обратного конуса. Построить тень, падающую от левой образующей АВ ниши на поверхность обратного конуса (рис. 1).

Рис. 1 - Построение тени, падающей от образующей АВ на поверхность обратного конуса: а) в пространстве, б) на ортогональном чертеже.

Рис. 1, а демонстрирует геометрическую суть построения тени от отрезка АВ на поверхность обратного конуса. Отрезок АВ и световой луч l образуют плоскость S общего положения. Контуром падающей тени будет линия пересечения этой плоскости с поверхностью конуса. На рис. 1, б представлено построение в ортогональных проекциях. Дадим объяснение одного и того же решения с двух разных позиций.

Позиционная задача. Строим линию пересечения плоскости S с поверхностью обратного конуса. Задачу решаем методом вспомогательных секущих плоскостей a и b. Строим линии пересечения вспомогательных плоскостей с конусом (окружности m и n) и секущей плоскостью (прямые a и b). Точки их пересечения будут принадлежать контуру падающей тени. Она будет иметь форму эллипса. Если конус усеченный, то получим дуги эллипса.

Теория теней. Задачу решаем методом горизонтальных экранов. Проводим экраны a и b, строим линию пересечения каждого из них с конусом (окружности m и n). Строим тень от образующей АВ на каждый экран (прямые a и b). При пересечении тени с окружностью получаем точки, принадлежащие контуру падающей тени.

В приведённом примере одному и тому же методу решения задачи даны два разных объяснения. Это показывает, что к решению одной и той же проблемы можно подходить с разных позиций.

Пример 2. Провести анализ разных методов решения одной и той же задачи. Дать их сравнительную характеристику. Предложить наиболее оптимальный вариант [2].

Задание. Имеется полусферическая ниша с открытым верхом в форме полуокружности (рис. 2). Требуется построить тень, падающую от этой полуокружности на внутреннюю поверхность ниши.

На рис. 2, а эта тень построена методом лучевых сечений. На контуре окружности берем несколько точек, проводим через них лучевые горизонтально–проецирующие плоскости и строим сечения в виде дуг эллипсов. При пересечении построенных дуг с лучами получаем точки контура тени.

Рис.2 - Построение падающей тени на сферическом куполе: а) методом лучевых сечний, б) методом горизонтальных экранов

На рис. 2, б задача решена методом горизонтальных экранов. Строим сечение сферы горизонтальной плоскостью и тень на нее от полуокружности. При пересечении двух построенных окружностей получаем точки контура падающей тени.

В этом примере методы построения разные, а полученный результат один и тот же. Второй способ, безусловно, рациональнее, так как требует меньше построений. Чертёж получается менее загруженным. Правда, здесь необходимо предварительно определить, в каких пределах можно проводить экраны. Верхний предел можно найти при помощи конуса с углом 35°, вписанного в полуокружность.

Пример 3. Изучили построение линейной перспективы по схеме Гаука. Желающим предлагается самостоятельно изучить метод архитектора и радиальный метод.

Задание. Построить перспективу одного и того же объекта тремя способами: радиальным, методом архитектора и по схеме Гаука. Провести хронометраж времени построения перспективы и дать оценку трудоёмкости каждого метода [3].

Предварительно студенты поэтапно разобрали построение перспективы точки каждым способом. Подсчитали количество затраченных операций и дали сравнительную характеристику каждого метода, обратив внимание на их положительные и отрицательные моменты. Затем приступили к эксперименту, в котором приняли участие 20 студентов.

По результатам эксперимента 65% участников отдали предпочтение схеме Гаука, 15% поставили на первое место метод архитектора, 15% отметили равнозначность методов Гаука и архитектора и 5% высказались за радиальный метод.

Таблица 1 – Средняя трудоёмкость построения перспективы разными способами и их оценка студентами по пятибалльной шкале

Студенты с желанием участвовали в эксперименте и сделали следующий вывод.

«В результате проведённой научно-исследовательской работы, которая включала в себя, как практическую, так и теоретическую часть, было установлено, что наиболее удобным и универсальным методом построения перспективы является схема Гаука. Результатом данной работы также стало освоение студентами первого курса различных методов построения перспективы, что, безусловно, является немаловажным как в контексте дальнейшего обучения, так и в контексте непосредственного ведения профессиональной деятельности» [3].

Пример 4. Перспективу изображают и архитекторы, и художники. Но их методы различны.

Задание. Выяснить, чем обусловлено это различие. Проанализировать на конкретных примерах.

Различие в методах построения перспективы архитекторами и художниками обусловлено стоящими перед ними задачами. Архитекторам важно передать документальный материал, точно соблюдая форму, размеры и расположение объектов. Их не интересует, как полученное изображение будет восприниматься глазом человека. Они используют линейную перспективу, построенную на геометрической основе. Возникла она в эпоху Ренессанса и называется ренессансной перспективой. Художники стараются передать образ субъективного пространства, т.е. таким, каким воспринимает его глаз человека. Такая перспектива называется перцептивной (от латинского слова «перцепция»- восприятие). Это две равнозначные перспективы. Зародились они одновременно, но теоретическое обоснование получили в разное время. Более подробно ознакомиться с результатами выполнения поставленного задания можно в публикации [4].

Таким образом, «углубляя» учебный материал, мы расширяем кругозор студента, знакомим его с различными приёмами проведения исследования, которые пригодятся ему в дальнейшем. Научно-исследовательская работа на первом курсе подготавливают стартовую площадку для старших курсов и будущего.

Литература

1. Денисов И. В., Козырев Н. В. Позиционные задачи и теория теней // Проспект Свободный 2015: материалы междунар. науч. конф. (15-25 апреля 2015) [Электронный ресурс] - Красноярск : Сиб. федер. ун-т, 2015.
2. Королёва А.А, Осипова А.Н. Анализ методов построения теней архитектурных форм // Проспект Свободный 2015: материалы междунар. науч. конф. (15-25 апреля 2015) [Электронный ресурс] - Красноярск : Сиб. федер. ун-т, 2015.
3. Емашкина А. А., Жавнер А. А., Пахомова В. И. Сравнительная характеристика методов построения перспективы // Молодёжь и наука: материалы Х Всерос. конф. - Красноярск: Сиб. федер. ун-т, 2014. - С. 77-81.
4. Баркалова В.В. Перспектива ренессансная и перцептивная // Студ. научн. форум 2015 [Электронный ресурс]. - Режим доступа: http://www.scienceforum.ru/2015/pdf/17415.pdf

References

1. Denisov I. V., Kozyrev N. V. Pozitsionnye zadachi i teoriya tenej // Prospekt Svobodnyj 2015: materialy mezhdunar. nauch. konf. (15-25 aprelya 2015) [Jelektronnyj resurs] - Krasnoyarsk : Sib. feder. un-t, 2015.
2. Koroleva A. A., Osipova A. N. Analis metodov postroeniya tenej arkhitekturnykh form // Prospekt Svobodnyj 2015: materialy mezhdunar. nauch. konf. (15-25 aprelya 2015) [Jelektronnyj resurs] - Krasnoyarsk : Sib. feder. un-t, 2015.
3. Emashkina A. A., Zhavner A. A., Pakhomova V. I. Sravnitelnaya kharakteristika metodov postroeniya perspektivy // Molodezh i nauka: materialy Х Vseros. konf. - Krasnoyarsk : Sib. feder. un-t, 2014. S. 77-81.
4. Barkalova V. V. Perspektiva renessansnaya i pertseptivnaya // Stud. nauchn. forum 2015 [Jelektronnyj resurs]. Rezhim dostupa: http://www.scienceforum.ru/2015/pdf/17415.pdf