ОПРЕДЕЛЕНИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ, ЯВЛЯЮЩЕЙСЯ СУММОЙ НЕСКОЛЬКИХ СЛУЧАЙНЫХ ВЕЛИЧИН
ОПРЕДЕЛЕНИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ, ЯВЛЯЮЩЕЙСЯ СУММОЙ НЕСКОЛЬКИХ СЛУЧАЙНЫХ ВЕЛИЧИН
Аннотация
Разработан алгоритм расчёта несобственных интегралов с параметром при вычислении дифференциальной и интегральной функций распределения случайной величины, являющейся суммой нескольких случайных величин с известными плотностями распределения. Результаты тестирования предлагаемых методов при относительно малых значениях второй производной подынтегрального выражения показали высокую эффективность использования численного метода средних прямоугольников с постоянной величиной интервала разбиения. Погрешность вычислений при числе интервалов n=100÷1000 в этом случае составляет около 10-4. Повышение n до 104÷105 снижает погрешность до 10-5÷10-15. Если вторая производная подынтегральной функции велика или определяется плотностью распределения для суммы более чем двух случайных величин, то потребуются более точные решения. Среди них отметим использование переменного интервала в сочетании, например, с методами Симпсона или Гаусса, обеспечивающими более высокую точность.
1. Введение
Пусть в области (∀z∈R) задана случайная величина T. Вероятность реализации случайного события, для которого выполняется условие T<t, определяется интегральной функцией распределения ,
Во многих случаях функция F(t) представляется несобственным интегралом от дифференциальной функции распределения случайной величины f(t)
где f(t) также может определяться несобственным интегралом.
Интегральная функция распределения непрерывна на отрезке её определения [-∞,b], в том числе для случая b=+∞, и при значении t, изменяющимся в области её определения, возрастает от 0 до 1. В ряде задач требуется найти дифференциальную функцию распределения случайной величины T, которая является суммой двух независимых случайных величин T=X1+Х2 с известными плотностями распределения f1(x1) и f2(x1). Известно, что дифференциальная функция f(t) для распределения T является свёрткой двух функций f1(x), f2(x) ,
Формула (3) легко обобщается на случай нахождения суммы трёх и более независимых случайных величин. В качестве примера найдём дифференциальную функцию f(t) для случайной величины T, являющейся суммой трёх случайных величин U=X1+Х2+Х3 с известными плотностями распределения f1(x), f2(x), f3(x). Поскольку плотность распределения суммы двух случайных величин X1+Х2 определяется формулой (3), то искомая плотность для трёх случайных величин равна
Несобственные интегралы (2)-(4) зачастую невозможно взять в явном виде, поэтому их значения рассчитываются численными методами, которые требуют использования значительных временных ресурсов. Поэтому исследование подобных ситуаций и разработка соответствующих оптимальных вычислительных методов имеет практический интерес. Настоящая работа посвящена рассмотрению алгоритмов численных методов, обеспечивающих расчёт интегралов типа (2)-(4) в задачах теории вероятности и математической статистики.
2. Методы и принципы исследования
Цель исследования – разработка алгоритма расчёта несобственных интегралов в теории вероятностей при вычислении функций распределения случайной величины. Для достижения цели необходимо провести анализ численных методов, используемых при вычислении интегралов, и рассмотреть решение следующих задач:
- выбрать алгоритм расчёта несобственных интегралов типа (2)-(4);
- определить погрешности выбранных алгоритмов при вычислении функций распределения случайной величины, зависящей от суммы случайных величин с известными плотностями распределения.
3. Основные результаты
3.1. Выбор алгоритма расчёта несобственных интегралов
Первый шаг при вычислении несобственных интегралов (2)-(4) связан с заменой бесконечных пределов интегрирования конечными значениями a и b, что позволяет перейти к вычислению определённого интеграла на отрезке [a, b]. Величины a и b зависят от функций распределения случайной величины и заданной погрешности вычислений ξ. Например, условие обеспечения точности определения дифференциальной функции (3) имеет вид
Потребуем, чтобы замена бесконечного предела при вычислении интеграла (2) обеспечивала расчётную погрешность не более ξ
Величина первого интеграла в условии (6) определяется точным значением интегральной суммы S
где – значение подынтегральной функции в точке ti*, принадлежащей i-му интервалу hi, ∑hi=tmax-tmin..
При вычислении интегральной суммы S значения нижнего и верхнего предела zmin, zmax выбираются таким образом, чтобы обеспечить необходимую точность расчёта ξ:
Поскольку значение F(z) принадлежит отрезку [0,1], то величина интегральной суммы при zmax должна удовлетворять условию:
Исходя из сказанного видно, что решение поставленной задачи сводится к вычислению интегральной суммы S. К настоящему времени разработаны эффективные методы её расчёта с достаточно высокой точностью. Один из них основан на использовании квадратурных формул Ньютона – Котеса , в котором для вычисления частичной суммы на каждом интервале hi подыитегральная функция представляется в виде интерполяционного многочлена Лагранжа. Наиболее простые квадратурные формулы реализованы в методах трапеции , левых, правых и средних прямоугольников и парабол . Они широко используются в учебном процессе и во многих прикладных задачах. В случае метода средних прямоугольников с постоянным шагом hi=h интегральная сумма S в формуле (8) представляется в приближённом виде
с обеспечением погрешности не более, чем величина
где n – число интервалов, zmin- zmax = nh, , f''(t*) – максимальное значение второй производной функции в точке t*∈[zmin, zmax].
В работе показано, что погрешность вычисления определённых интегралов для абсолютного значения второй производной |f''(t*)|≈1 при числе интервалов n=1000 составляет около 10-8. Подобная точность вполне приемлема при определении несобственных интегралов типа (2), (3), для которых подынтегральная функция достаточно точно выражается алгебраическим многочленом малой степени, обеспечивающим небольшую величину второй производной в формуле (11). Если вторая производная велика f''(t*) или определяется плотностью распределения суммы нескольких случайных величин, то можно воспользоваться тем же методом средних прямоугольников с переменным шагом hi. В этом случае интегральная функция (10) представляется в виде суммы
которая вычисляется для известной дифференциальной функции распределения на отрезке
Существует несколько способов формирования изменяющейся длины интервала, отслеживающей скорость изменения подынтегральной функции. Воспользуемся простой формулой
которая устанавливает размер последующего i+1-го интервала в зависимости от длины hi пропорционально уменьшению или увеличению первой производной в точке ti+1 по сравнению с её значением в начале этого интервала в точке ti.
В первом приближении значения производных можно вычислять по формулам
где значения δi, δi+1 – достаточно малые приращения, равные размеру интервала hi или меньше его.
Алгоритм определения интегральной функции распределения случайной величины, заданной несобственным интегралом (2), реализуется в следующем порядке:
А. Определение величины интервала разбиения области интегрирования. На первом этапе необходимо установить конечные области изменения параметров t и z в формуле (2), обеспечивающие возможность представления интегральной функции распределения для суммы двух случайных величин в виде
с погрешностью не более ξ.
В случае интегральной функции распределения для суммы трёх случайных величин области изменения параметров u, t и z в формуле (4) соответствуют условиям
Пример. Пусть требуется найти интегральную функцию для случайной величины T, являющейся суммой двух случайных величин X1 и X2 с известными плотностями распределения f1(x) и f2(x). Предположим, что область изменения функции f1(x) удовлетворяет условию x∈[x1min, x1max], а область изменения функции f2(x) - условию x∈[x2min, x2max]. Тогда областью изменения интегральной функции является x∈[x1min+x2min, x1max+x2max].
Б. Выбор численного метода интегрирования. На втором этапе следует выбрать численный метод расчёта интегралов. Во многих случаях самый простой метод средних прямоугольников может оказаться вполне приемлемым.
Если вторая производная подынтегральной функции велика или определяется плотностью распределения суммы нескольких случайных величин, то потребуются более точные решения. Среди них отметим использование переменного интервала в сочетании с методом Симпсона, что позволит снизить погрешность на четыре и более порядков .
В. Тестирование выбранного алгоритма. Оценка выбранного алгоритма предполагает обязательное тестирование путём сравнения полученных результатов с известными точными решениями.
3.2. Тестирование разработанного алгоритма и примеры определения функции распределения случайной величины, являющейся суммой нескольких случайных величин
Проверка предлагаемого алгоритма проводилась на двух различных функциях распределения с известными решениями:
- вычисление интегральной функции распределения случайной величины в соответствие с нормальным законом,
- определение дифференциальной и интегральной функции распределения для суммы двух случайных величин, подчиняющихся различным законам распределения.
Интегральная функция в случае нормального распределения случайной величины с математическим ожиданием a, равным 0, и среднеквадратическим отклонением, равным σ=1, имеет вид
Заменим несобственный интеграл (17) его приближённым значением
Подынтегральная функция в формуле (18) быстро снижается с увеличением |t| и при |t|→∞ асимптотически стремится к нулю. Можно показать, что замена интеграла (17) его приближённым значением (18) на отрезке [-5, +5] обеспечивает погрешность не более ξ=0.00006 . С целью повышения точности проведены вычисления в интервале t∈[-10,+10].
Результаты, полученные методом средних прямоугольников, представлены в таблице 1 для числа интервалов от 5 до 20.
Таблица 1 - Значения интегральной функции для нормального распределения с математическим ожиданием a=0 и σ=1 для различных z с использованием метода средних прямоугольников в зависимости от числа одинаковых интервалов n
z | n=5 | n=8 | n=10 | n=14 | n=20 |
-10 | 0,00000 | 0,00000 | 0,00000 | 0,00000 | 0,00000 |
-3 | 0,00060 | 0,00098 | 0,00110 | 0,00122 | 0,00128 |
0 | 0,49281 | 0,50000 | 0,50000 | 0,50000 | 0,50000 |
3 | 0,93862 | 0,99890 | 0,99934 | 0,99906 | 0,99887 |
4 | 1,14536 | 1,00070 | 0,99994 | 0,99998 | 0,99998 |
10 | 1,59684 | 0,91501 | 0,98562 | 0,99987 | 1,00000 |
Сравнение значений интегральной функции распределения случайной величины, представленных в таблице 1, с данными таблицы II в работе , где приведены значения вероятности в интервале z∈[-4,+4] с удержанием первых четырёх цифр после запятой, совпадают для вариантов вычислений в случае 14 и 20 интервалов с точностью до 10-4.
Определение погрешности реализованного алгоритма вычисления интегральной функции (17) путём замены её определённым интегралом (18) в интервале z∈[-10,+10] с использованием критерия точности (9) проводилось для числа интервалов n от 101 до 105. Результаты приведены в таблице 2.
Таблица 2 - Погрешность вычисления интегральной функции для нормального распределения с математическим ожиданием a=0 и σ=1 методом средних прямоугольников для различного числа одинаковых интервалов n при z=10
n | 101 | 102 | 103 | 104 | 105 |
Погрешность | 1,4·10-2 | 10-11 | 10-13 | 10-15 | <10-15 |
Проведённые расчёты показывают, что метод средних прямоугольников с постоянным интервалом обеспечивает высокую точность вычислений. Например, согласно таблицы 2, погрешность определения функции распределения случайной величины для 104 и 105 интервалов составляет не более10-15. Затраты машинного времени для числа разбиений n=105 не превышали одной секунды.
Обеспечение высокой точности расчётов в сочетании с малыми затратами машинных ресурсов связано с достаточно гладкой подынтегральной функцией в формуле (17), которая равна
Максимальная величина второй производной нормального распределения (17) достигается при z=0 и равна 1/√2π≈0,4. Следовательно, максимальная погрешность ζ достигается в нескольких интервалах, расположенных в окрестности точки z=0. В соответствие с формулой (11) величина погрешности εmax для одного такого интервала при n=104 составляет около 1,3·10-10. Абсолютное значение второй производной быстро падает по мере увеличения |z|.
Поскольку число интервалов с максимальным значением второй производной во много раз меньше по сравнению с количеством остальных интервалов, то общая погрешность расчёта интеграла будет на несколько порядков меньше εmax.
Данные таблицы 2 показывают, что погрешность ζ на 5 порядков ниже по сравнению с максимальным его значением ζmax для интервалов в окрестности z=0.
Проведём тестирование обсуждаемого метода на примере интегральной функции распределения для суммы двух случайных величин, подчиняющихся двум известным различным законам распределения. Пусть заданы две дифференциальные функции распределения случайной величины
для которых можно найти дифференциальную (3) и интегральную (2) функции распределения в аналитической форме.
После подстановки (19), (20) в выражение (3) получим следующие формулы, определяющие дифференциальную функцию f(t) для двух случайных величин:
Cумма двух случайных величин t, определяемая дифференциальными функциями (19), (20) для x<0, не может быть равной отрицательному числу. Поэтому вероятность события f(t), при котором t<0, равна нулю:
Дифференциальная функция (19) равна 1 на отрезке [0,1] и равна нулю вне этого отрезка. Следовательно, её величина отлична от нуля на отрезке [0,1] и определяется только плотностью второй случайной величины.
Значение x не может быть больше суммы двух случайных величин, равной t на отрезке [0,1]. Поэтому, исходя из вышесказанного, формула (3) преобразуется к виду
При t>1, формула (3) имеет вид
Функция распределения (3) для суммы двух случайных величин рассчитывалась двумя способами:
- с помощью численного метода средних прямоугольников с использованием интегральной суммы (10),
- с использованием точного аналитического решения (21)- (23).
Значения f(t), вычисленные двумя методами, представлены в таблице 3 для числа интервалов от 10 до 104.
Максимальная точность достигалась при n=104 с погрешностью в шестом знаке после запятой. Повышение количества интервалов до 105-106 не приводило к снижению погрешности.
Таблица 3 - Значения дифференциальной функции распределения суммы двух случайных величин, найденных по точным формулам (21) - (23), и вычисленные методом средних прямоугольников для постоянной величины интервалов на отрезке [0,15] в зависимости от числа интервалов n
t | n=10 | n=102 | n=103 | n=104 | Точное решение |
0,0 | 0,00000 | 0,00000 | 0,00000 | 0,00000 | 0,00000 |
0,5 | 0,39437 | 0,39355 | 0,39347 | 0,39347 | 0,39347 |
1,0 | 0,63788 | 0,63264 | 0,63217 | 0,63212 | 0,63212 |
1,5 | 0,40808 | 0,38579 | 0,38363 | 0,38342 | 0,38340 |
2,0 | 0,22164 | 0,23156 | 0,23244 | 0,23253 | 0,23254 |
3,0 | 0,10547 | 0,08747 | 0,08574 | 0,08556 | 0,08555 |
Тестирование используемого алгоритма свидетельствуют о достаточно высокой точности численных данных, полученных методом средних прямоугольников при определении дифференциальной функции распределения случайной величины. Согласно полученным данным погрешность расчётов находится на уровне 10-2 при n=10. По мере увеличения числа разбиений погрешность снижается до10-4 при n=1000 и до 10-5 при n=10 000.
Подстановка формул (21)-(23) в (2) позволяет найти аналитическое выражение для интегральной функции распределения суммы двух случайных величин
Результаты вычислений по точным формулам (24) и с использованием численного метода средних прямоугольников для постоянной величины интервала h на отрезке [0,15] представлены в таблице 4.
Таблица 4 - Значения интегральной функции, найденные по формуле (24) и вычисленные методом средних прямоугольников при n=100
z | 0,0 | 0,5 | 1,0 | 2,0 | 4,0 | 6,0 |
F(z), формула (23) | 0,000 | 0,106 | 0.367 | 0,767 | 0,968 | 0,996 |
F(z), численный метод | 0,000 | 0,106 | 0,366 | 0,766 | 0,968 | 0,996 |
Согласно данным в табл. 4 погрешность численного метода для интегральной функции распределения при n=100 составляет около 10-3, что на несколько порядков хуже по сравнению с нормальным распределением (таблица 2). Точность вычисления зависит от выбранного расчётного метода, количества интервалов и установленных пределов интегрирования [tmin, tmax] С целью оптимального выбора исходных параметров рекомендуется провести предварительные вычисления с использованием дифференциальной функции распределения f(t). В качестве примера в таблице 5 приведены рассчитанные значения f(t) в зависимости от n и tmax.
Таблица 5 - Вычисленные значения дифференциальной функции распределения f(t) (3) в зависимости от числа интервалов n при величине t, равного верхнему пределу tmax в области [tmin, tmax]
tmax | 5 | 10 | 15 | 20 |
n =102 | 0,0115776340013 | 0,0000780094843 | 0,0000005256238 | <10-15 |
n =103 | 0,0115776861008 | 0,0000780098353 | 0,0000005256261 | <10-15 |
n =104 | 0,0115776913108 | 0,0000780098704 | 0,0000005256264 | <10-15 |
Из таблицы 5 видно, что достаточно хорошие результаты достигаются при tmax≥5 и количестве разбиений n ≥102, обеспечивающих погрешность менее 10-8. Однако полученная точность меньше по сравнению с нормальным распределением (таблица 2), когда при n=102 погрешность составляет около 1011.
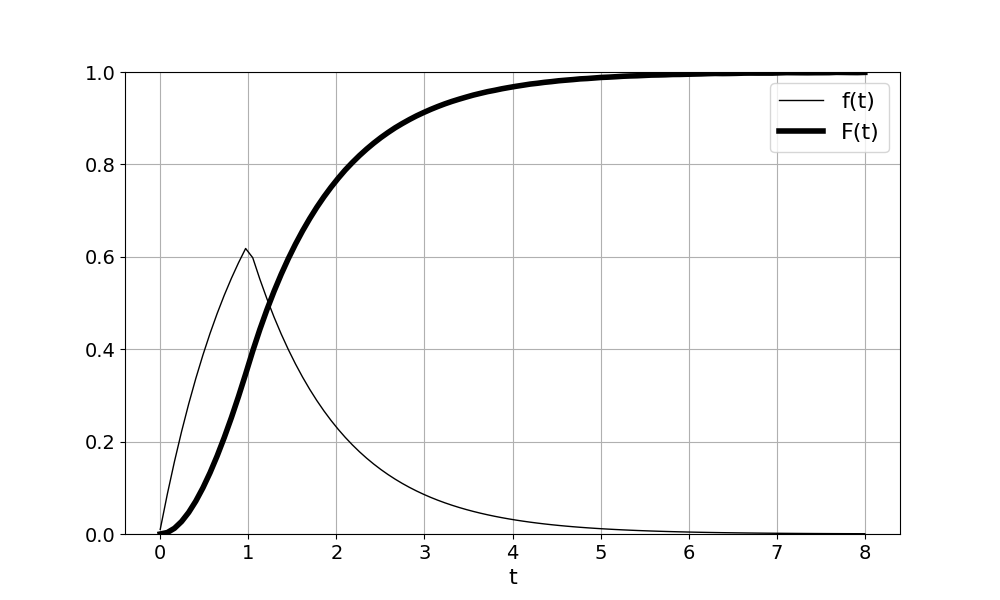
Рисунок 1 - Зависимость дифференциальной f(t) и интегральной F(t) функций распределения суммы двух случайных величин
4. Заключение
Проведён анализ численных методов расчёта несобственных интегралов, используемых в теории вероятности и математической статистике. Разработан алгоритма расчёта несобственных интегралов с параметром при вычислении дифференциальной и интегральной функций распределения случайной величины, являющихся суммой нескольких случайных величин с известными плотностями распределения.
Результаты тестирования предлагаемых методов при относительно малых значениях второй производной подынтегрального выражения показали высокую эффективность использования метода средних прямоугольников с постоянной величиной интервала разбиения. Погрешность вычислений интегральной функции при числе интервалов n=100÷1000 в этом случае составляет около 10-4. Повышение n до 104÷105 снижает погрешность до 10-5÷10-15 без существенных затрат времени выполнения кода программы.
Если вторая производная подынтегральной функции велика или определяется плотностью распределения для суммы более чем двух случайных величин, то потребуются более точные решения. Среди них отметим возможность использования переменного интервала в сочетании, например, с методами Симпсона или Гаусса, обеспечивающих более высокую точность.
