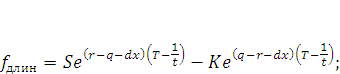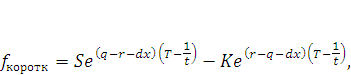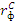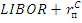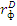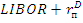ОСОБЕННОСТИ ПАРАДИГМЫ ПОСТРОЕНИЯ РЫНКА ПРОИЗВОДНЫХ ФИНАНСОВЫХ ИНСТРУМЕНТОВ СО СТАБИЛИЗИРУЮЩИМ БАЗИСОМ

Стрельников Е.В.

Кандидат экономических наук, Уральский государственный экономический  университет

ОСОБЕННОСТИ ПАРАДИГМЫ ПОСТРОЕНИЯ РЫНКА ПРОИЗВОДНЫХ ФИНАНСОВЫХ ИНСТРУМЕНТОВ СО СТАБИЛИЗИРУЮЩИМ БАЗИСОМ

Аннотация

В статье рассмотрено – экономическое значение некоторых финансовых инструментов на рынке и их роль в стабилизации положения на рынке. Так некоторые финансовые инструменты имеют определённый потенциал стабилизации, для примера инструменты имеющие «золотой базис». В статье рассмотрены некоторые финансовые инструменты с позиции установления стабильного состояния на рынке

Ключевые слова: финансовый рынок, парадигма построения финансового рынка, стабилизирующий базис.

Strelnikov E.V.

Pre-assistant professor, Ural State University of Economics

THE SPECIALIZATIONS TO ON PARADIGMALIC BUILDING DERIVATIVES MARKET TO STABLE BASIS

Abstract

The paper says to introduction of broadcast economical meaning to some market derivative instruments, its improve some financial instruments and role for stable to market. So many financial instruments has stable potential, for example «gold basis». There are a stable position up to market.

Keywords: financial market, paradigms to building financial market, non-stable, stabilization basis.

Рынок производных финансовых инструментов является относительно новым структурным элементом российского финансового рынка. Так, по мнению А. Н. Буренина, вертикальный срез рыночной экономики представлен только двумя сегментами:

1. спотовый рынок;
2. срочный рынок [1].

Например, вроде бы на всю простоту и непрезентабельность определений данный рынок состоит в основном из срочных контрактов. Так, несмотря на всю свою простоту, данный рынок является весьма сложным и развитым функционирующим сложным инструментом. На данном рынке обращается очень большое количество всевозможных финансовых инструментов. Например, функциональный спектр контрактов, которые обращаются на рынке, довольно велик и в реальности не сводится только к поставке реально произведенного продукта.

Рынок финансовых производных представляется весьма широким спектром торговых площадок и достаточно большим объемом сделок, происходящих на данном рынке. Другой вопрос, который нас в данный момент интересует, – это тот инструментарий, который обращается на рынке.

Так, по мнению М. Р. Скулкина, с наступлением XXI возникла новая форма неолиберализма; ее можно назвать ультралиберальной монетаристской моделью, позволяющей с помощью виртуализации финансового капитала превращать рыночные отношения в искусственно культивируемый механизм неэквивалентного обмена во всем мире, за которым скрывается внеэкономическое принуждение, ведущее к ограблению целых стран и народов [6. С. 271].

Как далее продолжает М. Р. Скулкин, понятие «виртуализация» вновь возникло на рубеже веков, его первое упоминание действительно было связано с некоторыми инструментами, вводившимися в оборот еще в Древней Греции. Например, экономический смысл виртуализации можно объяснить тем, что происходит как бы подмена реальных ценностей виртуальными, не существующими на самом деле.

Таким образом, организуется некий воображаемый мир, создаваемый сугубо искусственно, который как бы отрывает жизнь человека от реальной экономики, увеличивая его отдаление от реального сектора в экономике и повышая зависимость от данных, представляемых средствами массовой информации, в различной форме: виртуального продукта, виртуальной корпорации, виртуальных денег [6. С. 275].

Существует мнение, что виртуализация экономики имеет насколько форм, безусловно, и одной из них стало появление рынка финансовых производных. Логика у данной категории исследователей достаточно проста и она заключается в следующем.

Характеризуя виртуализацию, необходимо особое внимание обратить на перерождение виртуальной экономики в виртуальную экономику финансовых рынков, связанную с использованием производных финансовых инструментов, в частности деривативов.

Однако в данном споре не учитывается практически самый важный фактор: исходя из определения финансов, мы можем сделать вывод, что это уже виртуальная категория, т.е. процесс перераспределения денежных средств, априори не может носить материальный характер, сродни производству, например, кирпича или иного продукта.

Кроме того, не следует забывать, что действительно любой деривативный продукт получает свою стоимость от акции или иного финансового инструмента, который давным-давно виртуализовался. Так что если мы возьмем за основу эту формулировку, то остается загадкой, даже нонсенсом, как может деривативный продукт, имеющий в своей базе, например, акцию, являющуюся тоже предметом виртуализации, вдруг встать и мгновенно материализоваться. Таким образом, если несколько отойти от дискуссии по поводу фиктивности всей экономической системы мы сразу можем обратиться к сути тех вещей, рассмотрение которых нам необходимо^[1]. Так, если далее исследовать лемму Ито, то мы можем прийти к выводу, что на любом рынке существуют как сверхстабильная, так и сверхнестабильная зона. При этом стабильная зона может быть распространена на большую или меньшую часть рынка. В отношении стабильной зоны необходимо отметить, что она обеспечивает стабильность рынку.

Таким образом, необходимо достаточно точно определится с тремя основополагающими вопросами:

3. возможность существования в рамках процесса Ито базисного элемента, который показывал бы стабильное состояние на рынке;
4. определиться с основными, базисными понятиями используемыми на рынка финансовых производных;
5. вывести формулы финансовых производных нового типа, которые обладают на рынке стабилизирующим действием.

Таким образом, рассматривая ранее процесс Ито, мы пришли к выводу, что это на 100% стохастический процесс и что для изменения сути процесса необходимо добавить стабилизирующий элемент. Это также изменит, если полностью не дезавуирует процесс дестабилизации рынка.

Процесс Ито можно разложить в следующей последовательности. В частности, мы можем интерпретировать лемму Ито как вполне естественное обобщение более простых результатов, для этого нам необходимо рассмотреть функцию G.

Например, как нам известно, стоимость любого фондового актива, да и не только фондового, мы это уже мы ранее более подробно рассматривали сводно представить в виде функции, зависящей от базовой цены актива и времени изменения ценности актива. В общем если рассматривать более концептуально цену уже не базового актива а виртуализированного актива. Проблема виртуализации финансовых активов представляется очень важной и имеющей большое значение, по мнению некоторых ученых это стало одной из причин финансового кризиса [10]. Но возвращаясь к нашему более приземленному исследованию, рассмотрим непрерывную и дифференцируемую функцию G, всецело зависящую от переменной х. Так, мы можем представить если G – это результат деятельности на финансовом рынке, то 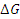 – это соответственно малое изменение функции G. Если это так, то, используя классический математический анализ, мы можем следующим образом разложить составляющую  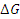[5. С. 163].

В результате мы получим, что неизменно малое изменение любого инструмента на финансовом рынке можно представить в виде:

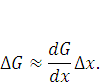(1)

Таким образом, величина любого финансового актива, имеющего более-менее реальный базисный элемент 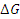, приблизительно равна скорости изменения G, умноженное на приращение переменной х. Ошибка этого равенства по теории Ито прямо пропорциональна величине 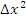. Если это так, то любой финансовый актив для большей точности можно представить в виде последовательности сообразно последовательности ряда Тейлора;

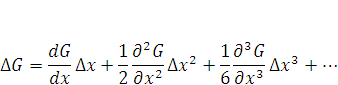(2)

Аналогичным образом мы можем построить ряд Тейлора и для двух переменных 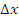 и 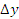, принципиального бы мы ничего не получили, просто оконечным уравнением стало бы выведение не односложного, а многосложного (двухкомпонентного) уравнения изменения функции доходности, т.е. dG, в данном варианте с двумя членами – это вышло бы следующим образом:

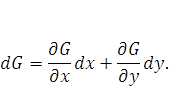(3)

Следовательно, если обобщим все полученные данные, то мы придем к выводу, что dx остается в поле стохастического влияния и не может быть рассмотрен как надежный и стабилизируемый факторный элемент, который зависимости от любого изменения t. Тот процесс, который мы только что в очередной раз рассмотрели, и представляется нестабильным процессом на финансовом рынке, доказательство этой нестабильности мы наблюдали довольно недавно [167]. Для того чтобы избежать подобных тенденций на финансовом рынке, нам необходимо ввести на одном из сегментов рынка «сверхстабильный» элемент, цена которого была бы вне подобной зависимости от dX и dt. В нашем варианте таким элементом вполне может стать сегмент рынка тезавраций. По нашему мнению, бриллианты или изумруды массой более 1,5–2,0 карата вполне бы могли стать таким обеспечением. Предположим, что мы вводим на рынок финансовых производных обеспечение в виде некого гаранта исполнения обязательств по производным финансовым инcтрументам. В этом случае dG и dt приобретают новые свойства, в частности свойства, назовем их так, сверхстабилизации. Суть сверхстабилизации в том, что при любом изменении t все остается неизменным; как следствие, dG стремиться к постоянному стабильному продолжению своего роста вне зависимости от каких-либо колебаний на рынке и фактически переходит в 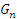. Принципиальным отличием первого от второго является то, что dG – это функция, которая представляется результатом броуновского движения на рынке, которое, как правило, мало чем ограничивается. В случае же с  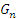мы имеем дело с трендовым направлением движения рыночной функции, базисом которой являются финансовые производные, закрепленные за драгоценными камнями. При такой диспозиции процесс Ито мы можем изложить в несколько другой плоскости.

Например, если ранее изменение переменной 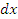 мы могли записать в виде

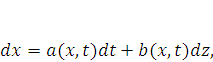(4)

то при использовании производных с золотым базисом мы получим несколько другую формулу:

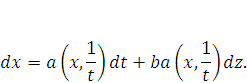(5)

Это впоследствии приведет к перестройке всего уравнения Ито с условиями золотого базиса:

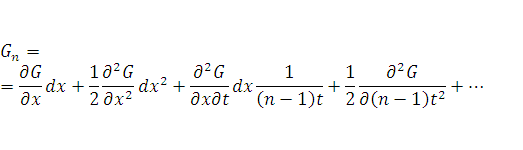(6)

Данная последовательность в итоге может быть преобразована в ряд Фибоначчи, который будет иметь свой определенный пределе приращения [7. С. 19].

Таким образом, мы получили общее уравнение стабилизации финансового рынка с использованием золотого базиса. В общем и целом золотой базис формулы предполагает минимальное изменение значения t на любом участке.  Для инвестора это означает, что стоимость его актива уже не будет представлять из себя dG, а превратится в сверхзащищенные активы  . Более подробно об активах рынка финансовых производных, имеющих золотой базис, мы будем вести разговор далее.

Для понимания терминологии предлагается определиться с основными понятиями производных финансовых инструментов.

Так, около 75% всех производных финансовых инструментов представляют гибридные вариации следующих финансовых производных.

Форвардный контракт (forward contract) – соглашение о купле-продаже определенного количества товара, государственных ценных бумаг, иностранной валюты или другого финансового инструмента по текущей цене (цене спот) с поставкой и оплатой в определенный момент в будущем. По той причине, что данный вид обязательства представляется уже окончательной сделкой (например, в отличие от опциона, держатель которого имеет право по своему усмотрению исполнять или не исполнять условия обязательства), то именно форвардный контракт с одной стороны может служить некой страховой защитой при реализации нестандартизированных и внебиржевых сделок. Однако даже при таких условиях иметь в обеспечении некого фиктивного обязательства другой не менее фиктивное обязательство представляется очень опасным.

Необходимо рассмотреть математическую структуру форвардного контракта. Но для этого нам необходимо сделать несколько вводных положений, которые будут касаться не только форвардных контрактов, но и любых иных производных финансовых инструментов.

Так, стороны форвардного контракта имеют совершенно равноправное положение, т.е. никто никому не платит. Это предполагает, что цена контракта будет равна заведомому неравноценному числу, т.е. равна нулю. Это в данной ситуации показывает определенную рискованную составляющую. Но не стоит забывать о том, что практически любая финансовая производная может иметь «золотое обеспечение», которое и будет являться неким стабилизирующим фактором.

В частности, следует учитывать, что в процессе исполнения форвардных контрактов мы можем столкнуться с тремя типичными случаями:

1) форвардный контракт, не приносящий доходов;

2) форвардный контракт, приносящий определенные доходы;

3) форвардная цена активов, приносящих постоянные дивидентные платежи.

Практически все три варианта имеют много схожих моментов в процессе ценообразования, но с позиции хеджирования лучше рассмотреть вариант, когда форвардный контракт приносит определенный доход. На необходимо сразу отметить, что в этом случае мы коснемся сразу несколько областей срочного рынка [11].

Для цены биржевого контракта мы получаем следующую ценовую модель:

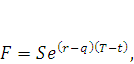(7)

где S – спот-цена активов в текущий момент времени t; Т – дата поставки активов; r – безрисковая процентная ставка на срок 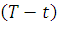 лет при непрерывном начислении; q – постоянная дивидендная доходность.

Однако, как уже ранее было отмечено, r из безрисковой процентной ставки может легко превратиться в сверхрисковую, в случае колебаний, например, на ссудном рынке. В этом случа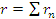е , где 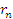 – это совокупность возможных процентных ставок, изменяющихся согласно стохастическим правилам.

Предположим, что мы вводим такое понятие, как золотой базис в отношении форвардных контрактов, по своей экономической сути это будет означать стабильный актив, введение которого будет постоянно вести к планомерному увеличению стоимости форвардного контракта на величину 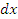 и некоторому изменению временного фактора, т.е. замене t на 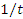. В частности,  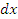будет представлена в виде укрепления базисного актива, а  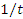будет представлено интервалом времени, в течение которого возможно изменение цены «золотого базиса». В частности, о подобной структуре рынок уже давно нам сигнализирует всеми возможными методами [9].

Мы можем привести две основные формулы для форвардных контрактов – для длинных позиций и для коротких позиций^[2].

Так, с условием введения золотого базиса формула будет выглядеть следующим образом:

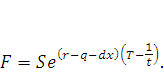(8)

Для примера следует привести примеры формул для форвардных контрактов для длинных и коротких позиций.

(9)     (10)

где К – цена исполнения сделки.

Данные формулы действуют для валютного рынка, и если рассчитать по ним, например, шестимесячную форвардную цену английского фунта, если текущий обменный курс был равен 1,83, а безрисковые процентные ставки в США и Англии были равны 6 и 4%, при этом курс бриллиантов с характеристиками выше среднего и массой 2,0–2,5 карата не подвергся дюрации более 1%. Аналогичная ситуация может наблюдаться и на других рынках, на которых применяется форвардная схема взаимоотношений, и на фьючерсных рынках. По своей сути фьючерсный рынок представляет собой один из видов совокупности форвардных сделок.

Таким образом, форвардный актив с золотым базисом можно представить в виде следующей пропорциональной формулы:

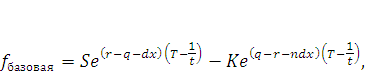(11)

где n – количественный состав или увеличенное стоимостное выражение драгоценных камней, входящих в золотой базис.

Кроме того, заключение форвардных контрактов происходит на фьючерсных условиях, это сам собой даже очевидно наблюдаемо из определения как форвардного, так и фьючерсного контрактов. В частности, если форвардным контрактом называется соглашение о купле-продаже, то фьючерсным контрактом уже является договорное обязательство, которое по своей как экономической, так и юридической природе является договором – идентичным видом обязательства. Следовательно, базовая формула для введения в оборот такого стабилизирующего фактора, как золотой базис, вполне применима и для фьючерсных контрактов. Но несмотря на такое универсальное свойство, для фьючерсных контрактов может быть уместна и несколько иная формула.

При этом, по мнению В. Е. Барбаумова, для одного и того же актива может существовать одновременно две цены – форвардная и фьючерсная. Будем считать это особенностью рынка финансовых производных [8. С. 134]. Однако это действительно при следующих условиях:

1) отсутствуют трансакционные расходы и налоги;

2) на форвардном и фьючерсном рынках инвесторы могут занимать длинные и короткие позиции на любые количества активов, то иногда существуют и ограничения в рамках биржевой торговли;

3) все инвесторы обладают достаточным капиталом (или кредитом), чтобы выполнить в случае необходимости все требования по марже;

4) отсутствуют прибыльные арбитражные возможности;

5) существует безрисковая процентная ставка, причем она одинакова для всех сроков и не меняется во времени.

Именно вследствие перечисленных причин цены на форвардных и фьючерсных позициях должны совпадать. Если внимательнее посмотреть на вышеперечисленные условия, то мы увидим, что для рынка важен определенный стабилизирующий фактор, который и позволит ценам находиться в стабильном положении.

В нашем случае введение золотого базиса стабилизирует положение и позволит заменить практически все перечисленные факторы, стремящиеся к нестабильности.

Фьючерсный контракт (futures contract) – договорное обязательство, при котором посредством применения схемы купли-продажи определенное количество товаров некого финансового инструмента по фиксированного цене в момент заключения контракта, по цене со сроком исполнения в определенное время в будущем. Если рассматривать экономические отношения по данному виду финансовой производной, то сделка предполагает оплату денежной суммы за товар или за акцию, либо за иной финансовый инструмент через определенный промежуток после заключения сделки по цене, установленной в контракте. Так, основной целью фьючерсной сделки представляется не получение разницы в ценах на предмет купли-продажи (соответствующий финансовый актив), возникающей к ликвидному сроку (сроку завершения сделки), а именно хеджирование позиции покупателя с целью сохранения стабильности товарного оборота. В частности, фьючерсный контракт позволяет участникам международной торговли хеджировать свои риски, что с успехом используют представители Поднебесной, чей товарооборот за последний год вырос на 23%, немалую роль в этом сыграла существующая система хеджирования поставочных контрактов [13].

Таким образом, как мы уже говорили, для фьючерсных контрактов вполне может подойти и формула для форвардных контрактов, особой ошибки при ее использовании мы не видим. Несмотря на это, даже при соблюдении всех указанных факторов или введении золотого базиса мы можем вывести самостоятельную формулу фьючерсного контракта с золотым базисом.

В любом случае на рынке фьючерсных контрактов имеет также место следующее равенство:

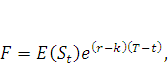(12)

где F – фьючерсная цена активов на момент времени t; Т – дата поставки активов; 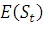 – ожидаемая спот-цена активов на дату поставки активов; r – ожидаемая доходность рассматриваемых активов за период от t до T.

В целом приведенное равенство нам показывает, что на фьючерсном рынке активы во многих случаях могут служить оценкой ожидаемой в будущем спот-цены в отношении данных инструментов. Например, если финансовые активы буду резко положительно или отрицательно коррелировать с рыночными показателями, то фьючерсная цена данных активов будет либо меньше, либо больше ожидаемой спот-цены. В этом случае мы опять стал­киваемся с проблемой неопределенности и, как следствие, с проблемой дестабилизации рынка финансовых производных и всего финансового рынка.

Однако если мы введем понятие «золотого базиса», т.е. некого актива в виде драгоценного камня, цена на которые не может так быстро изменяться, то по аналогии с форвардной ценой мы получим следующую формулу:

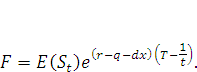(13)

В данном случае мы получим стабильно предсказуемую цену, которая не будет изменяться согласно стохастическому закону, а будет лишь стабилизировать рынок финансовых производных. Степенной множитель, его экономическое значение в этом случае будет полностью идентичным значению в формуле форвардного контракта, предложенной ранее (в этом случае рынок получает практически стабильную возможность развития фьючерсного рынка в парадигме 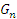). Подобным образом будут изменяться формы фьючерсных контрактов на фондовые индексы и на иные пространственные финансовые инструменты. В частности, это фьючерсные контракты на фондовые индексы или на иные не существующие в реальности финансовые активы. В данном случае золотой базис будет играть роль двойного обеспечения.

Опционом (option) можно назвать обусловленное договорное соглашение для одной их сторон выбрать способ, объем исполнения обязательства или отказаться от его исполнения при оговоренных обстоятельствах. За полученное право выбора покупатель опциона оплачивает продавцу некоторое вознаграждение, называемое премией. При этом продавец опциона обязан исполнить контрактное обязательство, если держатель решает его исполнить. Подобное соглашение, подготовленное его продавцом, предлагает покупателю право (но не обязательство) либо заказать поставку определенных ценных бумаг в течении указанного периода (например последующих 8 месяцев), либо поставить ценные бумаги или иные финансовые инструменты продавцу опциона на момент окончания действия опционного соглашения или рассматриваемого временного периода. В настоящее время существует два основных типа опциона – «на покупку» (опцион колл), который дает право держателю купить предмет торга – финансовый актив, также существует в практической деятельности и опцион, который дает право держателю купить рассматриваемый актив, и «на продажу».

Более того, практически все опционы можно разделить на три категории: опцион «в денежном эквиваленте», опцион «при денежном эквиваленте» (т.е. при немедленном исполнении, что выразится в нулевом притоке средств для опциона, так как цена исполнения для обоих видов опционов будет равна текущей стоимости), также применяется и опцион «без денег» (в случае его немедленного исполнения сделка приведет инвестора к денежным расходам). Опционная торговля представляется одной из наиболее развитых форм, позволяющих нарастить большую долю спекулятивного капитала, что несомненно отражается и на торговых балансах ведущих стран мира, в том числе на их валютной политике [12].

В случае с опционами как с американским, так и с европейским типом мы вынуждены несколько разделить свою тактику. Например, рассмотрим случаи с европейскими опционами. Однако для того чтобы приступить к анализу данного вида финансовых производных, необходимо сделать некоторые вводные (условия):

а) рынки, на которых происходят торговые сделки близки к совершенным, т.е. к ним применимы следующие пропорции: рынки должны отвечать признакам совершенства (отсутствуют транзакционные расходы и налоги; ни один инвестор, покупая или продавая активы, не может повлиять на цены; разрешены короткие продажи);

б) участники рынка могут неограниченно кредитовать или занимать деньги под одну и ту же безрисковую ставку  (при непрерывном начислении);

в) по форвардным сделкам отсутствует кредитный риск;

г) отсутствуют прибыльные арбитражные возможности, т.е. нельзя получить будет безрисковый доход за счет различия цен на активы.

Кроме того, следует учитывать, дополнительные обстоятельства:

6. существует возможность брать ссуды или кредитовать, под соответствующую (по срокам) безрисковую процентную ставку;
7. отсутствуют прибыльные арбитражные возможности.

Таким образом, обычная формула для европейских опционов будет выглядеть следующим образом:

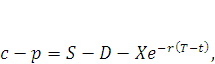(14)

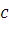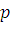где  и  – стоимость текущих европейских опционов «колл» и «пут» соответственно на одни и те же активы с ценой исполнения  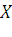при дате исполнения 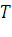, то имеет место некий паритет цене, который может быть в крайне редких случаях;  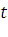– текущий момент времени; S – стоимость базисных активов в момент t; D – приведенное значение доходов, поступающих от активов за время от  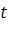до 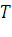; 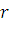– безрисковая процентная ставка при непрерывном начислении по инвестициям на  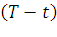лет.

В целом данная формула, как и формула для американских опционов, не учитывает нестабильность рынка, типичным примером может служить ситуация складывающаяся сейчас в еврозоне, где немалую роль нестабильности добавляют именно финансовые производные подобного рода [14]. Как уже ранее говорилось, во многих формулах, описывающих финансовые производные, мы не встречаем основного – того, что может и должно принести стабильность на рынок, т.е. мы не видим, как опционы могут стабилизировать положение на рынке. Для стабилизации рынка нам необходимо ввести значение некой функциональной производной, которая бы стабилизировала весь рынок – как при помощи европейских, так и при помощи американских опционов. Данным стабилизатором должен стать золотой базис, который как раз вписывается в построение парадигмы 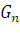. В этом случае мы вводим формулу золотого стабилизатора как фактора торможения и стабилизации стохастических процессов  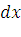(стоимостное выражение «золотого стабилизатора»).

Формула должна выглядеть следующим образом:

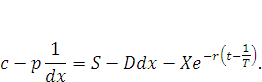(15)

В таком случае мы получаем общее уравнение для опционов, содержащих золотой базис, который будет всегда стабилизировать контракт и неким образом «привязывать» его к стабильному базису ценовой характеристики драгоценного камня. Это, безусловно, снизит возможности для арбитражных сделок с данным активов, но зато это позволит сверхстабилизировать хеджирующий инструмент на финансовом рынке. Это создаст очень стабильнейший инструмент, не изменяющий в цене даже в относительно короткие сроки.

Своп (swap) – обязательство, заключающееся в обмене товарами, ставками процента по финансовому обязательству или валюты на любой другой товар, ставку процента или валюту. Существует огромное видовое многообразие своповых контрактов. Не следует забывать, что одним из основных дестабилизирующих факторов представляется именно наличие слишком вольных условий для своповых сделок, в частности это касается валютных обязательств, которые прямым образом ведут к увеличению инфляционных тенденций в экономике. Хотя следует отметить, что инфляция представляется очень важным проблемным моментом, для удержания которой и служат своповые обязательства, которые к сожалению. Не так часто используются в современной экономике. Однако, как при валютном, так и при инфляционном таргетировании использование своповых схем может принести непоправимый вред [4. C. 94].

Наиболее часто употребляемыми и используемыми с нашей точки зрения могут представляться процентные и валютные своповые контракты. Например, в сложившейся ситуации с экономикой Японии вполне будет применим вариант того же самого процентного свопового контракта [15]. Так, если уточнить определение, то мы придем к пониманию, что процентным своповым контрактом будет называться соглашение об обмене потока будущих платежей от других активов. Это зависит от того, какие активы будут положены в основу свопового контракта. Именно поэтому и делается принципиальное различие между двумя вышеперечисленными типами своповых сделок. Например, в случае с процентным свопом производится обмен процентных платежей от условий основной суммы займа с фиксированной процентной ставкой.

Кроме того, во многих процентных свопах плавающая процентная ставка достаточно жестко привязана к ставке предложения на лондонском межбанковском рынке, например, шестимесячных евродолларовых депозитов. Эта конструкция рассматривается экономикой как сверхнадежная структура, в которой не может быть никаких провалов или просадок. Однако в существующей посткризисной ситуации и в частности это связано с ситуацией на валютном рынке Европы [13].

Так, на ссудном рынке может сложиться следующая ситуация, а именно подобная ситуация и может иметь место. Например, на ссудном рынке двум компания C и D необходимы займы на определенный срок в размере Q. Юридическое лицо С просто нуждается в займе с плавающей процентной ставкой (подобные займы имеют большое распространение и их необходимость для экономики всем очевидно, они используются для финансирования оборотного капитала [3. С. 176]). В свою очередь, компания D с фиксированной ставкой – подобные займы используется для финансирования крупных инвестиционных проектов.

Таким образом, на рынке капитала складывается следующая ситуация:

Компания	Фиксированная ставка	Плавающая ставка
С
D

В нашем случае стабилизирующим фактором может стать ставка 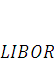 – но на самом деле в современной ситуации данная ставка может стать дестабилизирующим фактором, так как для всего рынка потому что при этом должны соблюдаться следующие условия:

1) 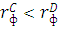, , 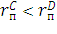т.е. мы предполагаем, что кредитный рейтинг компании С значительно выше кредитного рейтинга компании D, именно поэтому компания С обладает наибольшим преимуществом на рынках. Но это касается только рынка твердых ставок, на рынке плавающих кредитных ставок ситуация складываться с точностью до наоборот; это и будет вторым условием:

2) 

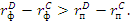
Далее предположим, что компания С – это достаточно крупное юридическое лицо, которое может привлекать средства за счет эмиссии облигаций с фиксированным процентом, в свою очередь компания D этого сделать не сможет, но она более известна местному банку, который без проблем выдаст ей кредит с плавающей процентной ставкой. В таком случае возникает практически идеальная ситуация когда можно провести операцию по построению процентного свопа.

Подобную операцию можно представить в виде следующей системы уравнений:

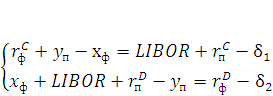(16)

Данная система линейных уравнений и представляет собой именно обмен процентными операциями, однако давайте рассмотрим уравнение с позиции стабильности финансового рынка, в случае если главный стабилизирующий фактор – ставка 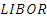 перестает быть неким стабилизатором положения, то мы получаем сверхненадежную систему, которая готова к спекулятивным стратегиям.

Кроме того, уравнение может быть применимо только в том случае, если выдерживается равенство

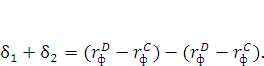(17)

Однако такая система является еще более сверхнестабильной, так как фактор стабилизации, как мы уже выяснили, таковым быть не может из-за крайней ненадежности и спекулятивности рынка. В концепции стабилизации предполагается введение золотого базиса как элемента стабильности сделок на финансовом рынке, в частности на рынке финансовых производных.

Нам рынке своповых контрактов должна быть создана система поддерживающая своей ликвидностью как ставки ссудного рынка в виде хорошо известной ставки 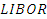 или любой иной процентной ставки по которой и будет производится обмен.

В этом случае равенство дисперсий следует «усилить» на величину сверхмалого хаотичного изменения стоимости драгоценного камня .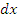

Следовательно, уравнение сложения дисперсий примет следующий вид:

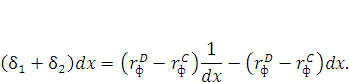(18)

Кроме того подобное «усиление» формулы отношения дисперсий в подобных схемах вполне приемлемый шаг и он часто используется в портфельной теории [2. C. 118].

При этом само уравнение своп обмена будет уже представляться в следующем виде:

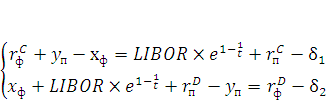(19)

Так, мы получаем несколько другую формулу, рассчитанную на то, что она будет именно действительным фактором стабилизации на любом сегменте финансового рынка, на котором будет применяться система своповых операций. Например, на рынке ипотечных облигаций с покрытием данная формула обеспечит нарастить ликвидность массовому сектору мелких компаний, дающих ликвидность целому сектору на ссудном рынке [15].

Таким образом, одним из основных, если не самым главным фактором на рынке, которые приведут к стабилизации, является стабильное развитие рынка финансовых производных, которые должны базироваться на самовозрастающей цене драгоценных камней, формирующих золотой базис, хеджирующих практически все риски инвестора и при этом уменьшающих риск самопроизвольного увеличения арбитражных операций.

Концепция развития поведения финансового рынка должна строиться на новой трактовке уравнения Ито. Это и есть один из способов развития финансового рынка, который принесет долгожданную стабилизацию.

Таким образом, в работе рассмотрены основные и ключевые базисные финансовые производные, все остальные следует рассматривать как функцию от других финансовых инструментов.