КОМПАКТНЫЕ ДЕТЕРМИНИСТИЧЕСКИЕ ГИБРИДНЫЕ СТРУКТУРЫ НА ОСНОВЕ ДВУХ ВЗАИМОПРОНИКАЮЩИХ ФРАКТАЛЬНЫХ ПОДРЕШЕТОК НА КВАДРАТНОЙ СЕТКЕ

Иванов В.В.

Кандидат химических наук, доцент, Южно-Российский государственный технический университет (Новочеркасский политехнический институт)

КОМПАКТНЫЕ ДЕТЕРМИНИСТИЧЕСКИЕ ГИБРИДНЫЕ СТРУКТУРЫ НА ОСНОВЕ ДВУХ ВЗАИМОПРОНИКАЮЩИХ ФРАКТАЛЬНЫХ ПОДРЕШЕТОК НА КВАДРАТНОЙ СЕТКЕ

Аннотация

Обсуждается возможность формирования компактных детерминистических гибридных структур на основе двух взаимопроникающих фрактальных решеток на квадратной сетке

Ключевые слова: модуль, гибридный генератор, фрактальная структура.

Ivanov V.V.

PhD in Chemistry, associate professor, South-Russian state Еngineering University (Novocherkassk Polytechnic Institute)

COMPACT DETERMINISTIC HYBRID STRUCTURES BASED ON TWO INTERPENETRATING FRACTAL SUB-LATTICES ON SQUARE NET

Abstract

The forming possibility of the compact deterministic hybrid structures based on two interpenetrating fractal sub-lattices on square net is discussed.

Keywords: module, hybrid generator, fractal structure.

При инъективном способе генерирования фрактальной структуры в 2D пространстве ее генератор, заданный в единичной ячейке [0…1; 0…1] квадратной сетки, определяет особенности строения и основные свойства локального фрактала [1, 2]. Позиционное и ориентационное упорядочение этих фракталов во всем ячеистом пространстве приводит к образованию детерминистической фрактальной структуры, представляющей собой бесконечное множество локальных фракталов [3 - 12]. Условие структурной совместимости фрактала с пространственной ячейкой и аналогичными фракталами-соседями определяет периоды идентичности и параметры элементарной ячейки детерминистической структуры [6, 8, 12].

Одно из условий получения фрактальных структур с минимальными периодами идентичности – симметричность генераторов локальных фракталов. В этом случае могут быть получены детерминистические структуры с параметрами элементарной ячейки, совпадающие с параметрами единичной пространственной ячейки. К числу таких фрактальных структур в 2D пространстве относятся фрактал Вичека (FV), фрактал на основе канторова множества точек (CM²), ковер Серпинского (CS) [1, 2]. Свойства образующихся фрактальных решеток в пространственной ячейке в каждом случае определяют соответствующие спектральные характеристики и размерность фрактала (табл.1) [6, 8].

Таблица 1 – Свойства некоторых симметричных фракталов с К = 1/9, сформированных в квадратной ячейке 2D пространства.

Наименование	Генератор	DimL	Симметрия структуры, G22	DimG
Множество канторовых множеств	Gen(CM2)	1,262	p4mm	2
Фрактал Вичека	Gen(FV)	1,465	p4mm	2
Ковер Серпинского	Gen(CS)	1,893	p4mm	2

Рассмотрим возможность формирования более компактных генераторов, составляя их из двух генераторов фракталов с одинаковым коэффициентом подобия К и задавая в пространственной квадратной 3х3-ячейке в лакунарных подпространствах каждого из них. Будем считать, что оба генератора не взаимодействуют, т.е. их действие распространяется только на ту часть ячейки, которую они занимают в составном генераторе. В этом случае очевидно. что для каждого из их подфракталов доля лакунарного пространства существенно меньше, чем в соответствующих одногенераторных подфракталах (рис.1).

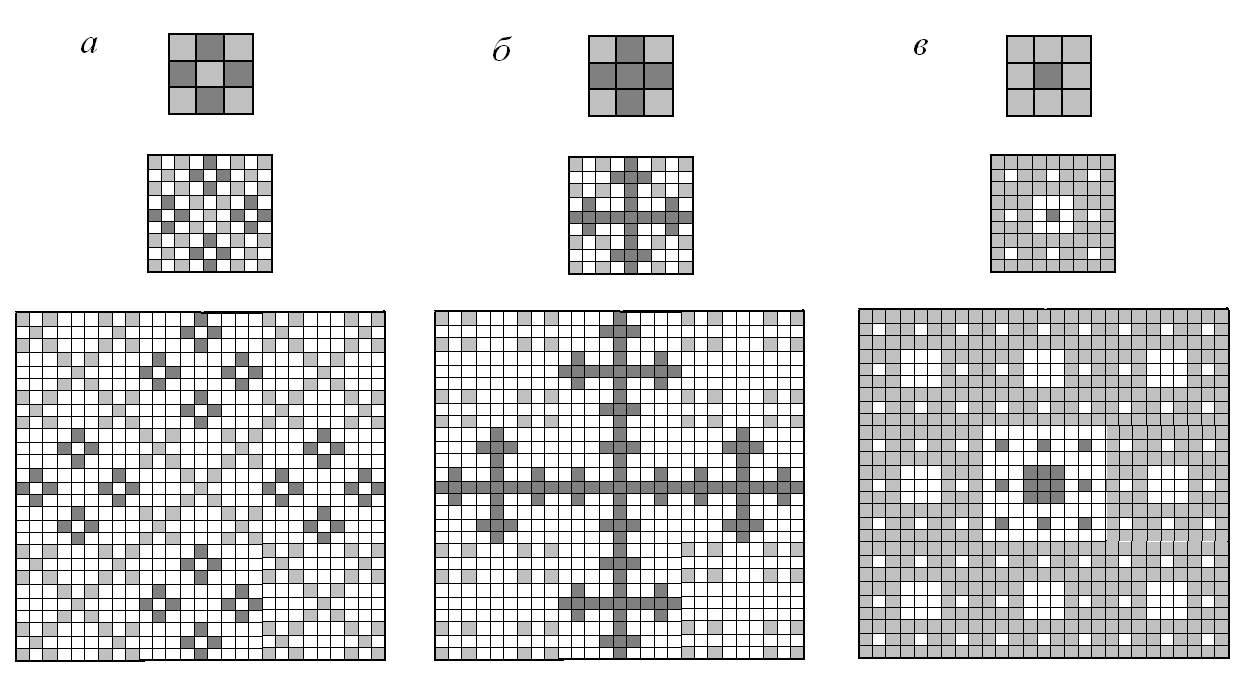
Рис.1 – Изображения гибридных генераторов (FV+Rh) (а), (CM²+C) (б), (CS+P) (в) и соответствующих им предфракталов 2-го и 3-го поколения в квадратной единичной ячейке 2D пространства.

Средневзвешенная локальная размерность компактного фрактала с гибридным генератором F(GenF₁+GenF₂) (табл.2) определяется следующим образом:

<Dim_L> = Dim_L F(GenF₁+GenF₂) = K[N₁ Dim_L (GenF₁) + N₂ Dim_L (GenF₂)],

Dim_L (GenF_i) = (lnN_i / ln(K^-1/2))

где N₁ и N₂ - числа занятых подъячеек в соответствующих генераторах, (N₁+N₂) = K^-1.

Отметим, что все полученные компактные гибридные фракталы симметричны, описываются плоской группой G²₂ = p4mm и имеют фрактальные размерности между среднеарифметическим и среднегеометрическим значениями размерностей соответствующих пар простых фракталов (табл.2).

Таблица 2 – Свойства некоторых симметричных гибридных фракталов, компактно сформированных в квадратной ячейке 2D пространства.

Наименование	Гибридный генератор	<DimL>	Симметрия структуры, G22	DimG
Фрактал Вичека и Ромб (Rhombus)	(FV+Rh)	1,375	p4mm	2
Множество канторовых множеств и Крест (Cross)	(CM2+C)	1,375	p4mm	2
Ковер Серпинского и Точка (Point)	(CS+P)	1,893	p4mm	2

Полученные данные о компактных детерминистических гибридных фрактальных структурах могут быть использованы при интерпретации трибологических свойств поверхности композиционных материалов и покрытий [12-15], межмодульного и структурного синергизма в неорганических ионопроводящих материалах [16, 17].