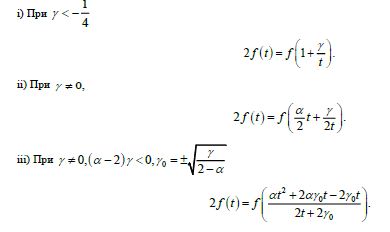О РЕШЕНИИ УРАВНЕНИЯ ШРЁДЕРА СПЕЦИАЛЬНОГО ВИДА

О РЕШЕНИИ УРАВНЕНИЯ ШРЁДЕРА СПЕЦИАЛЬНОГО ВИДА

Научная статья

Кальницкий В.С.¹, ^*, Петров А.Н.²

¹ ORCID: 0000-0002-3937-6078;

² ORCID: 0000-0001-6853-5480;

¹ Санкт-Петербургский государственный университет, Санкт-Петербург, Россия;

² Военная академия материально-технического обеспечения имени генерала армии А. В. Хрулёва, Санкт-Петербург, Россия

^* Корреспондирующий автор (st006987[at]spbu.ru)

Аннотация

Классификация обобщенных уравнений Бетхера второго порядка от двух аргументов, в результате классификационной теоремы, полученной ранее авторами, была сведена к 13 каноническим функциональным уравнениям, соответствующих орбитам действия общей линейной группы на пространстве тензоров типа (2,1), симметричных по ковариантным индексам. Оставшиеся не решенными пять канонических уравнений были сведены к вещественным уравнениям Шрёдера от одной переменной, которые интерпретируются как вопрос о вещественной сопряженности многочлена 𝑡 2 и некоторой рациональной функции (ядра). В данной статье для четырех уравнений доказана тривиальность любого непрерывного решения и для одного оставшегося уравнения доказана тривиальность вещественно-аналитического решения.

Ключевые слова: уравнение Бетхера, уравнение Шрёдера, функциональное уравнение.

ON THE SOLUTION OF THE SCHROEDER EQUATION OF A SPECIAL FORM

Research article

Kalnitsky V.P.¹, ^*, Petrov A.H.²

¹ ORCID: 0000-0002-3937-6078;

² ORCID: 0000-0001-6853-5480;

¹ Saint Petersburg State University, Saint-Petersburg, Russia;

² Military Educational Institution of Logistics named after General of the Army A.V. Кhrulyov, Saint-Petersburg, Russia

^* Corresponding author (st006987[at]spbu.ru)

Abstract

The classification of the generalized second-order Böttcher's equations from two arguments, as a result of the classification theorem established earlier by the authors, was reduced to 13 canonical functional equations corresponding to the orbits of the action of a general linear group on the space of tensors of type (2,1) symmetric by covariant indices. The remaining five canonical equations were reduced to the real Schröder equations of one variable, which are interpreted as a question of the real conjugacy of the polynomial 𝑡 2 and some rational function (kernel). In this article, the triviality of any continuous solution is proved for four equations and the triviality of a real-analytical solution is proved for one remaining equation.

Keywords: Böttcher's equation, Schröder's equation, functional equation.

Основные определения

В работе авторов [1] было завершено исследование решений обобщенных уравнений Бетхера [2] второго порядка от двух аргументов, начатое ранее в [3]. С использованием метода базовых решений [4] были описаны классы гладких решений таких уравнений, определённых на некоторой конической области с вершиной в начале координат. Решающим оказался метод прямого описания орбит действияобщей линейной группы на пространстве тензоров типа (2,1), симметричных по ковариантным индексам. Было доказано, что любое обобщённое уравнение Бетхера второго порядка приводит к одному из тринадцати типов уравнений, соответствующих тензорам, названных авторами каноническими. Часть обобщённых уравнений Бетхерабыла решена полностью и остальная часть сведена к трём однопараметрическим и двум двухпараметрическим семействам функциональных уравнений Шрёдера [5] от одной переменной, которые удалось решит лишь частично, опираясь на методы, описанные в работах [6], [7], [8].

Определение 1 [1, С. 217].Функциональное уравнение вида

где s – константа, 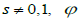– функция с областью определения 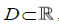, называется уравнением Шрёдера.
Функция 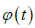 называется ядром. Решение ищется в классе непрерывных на  функций.

В нашем исследовании функция – функция вещественного аргумента. В дальнейшем мы будем предполагать,
что область задания ядра является всей прямой без конечного множества точек 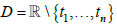Решение уравнения
Шрёдера в комплексном случае обсуждается, например, в [2].
Определение 2. Композицию k функций 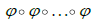 будем называть композиционной степенью и обозначать  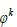. При этом  – обратная функция, если она существует.

Определение 3. Орбитой точки t называется множество 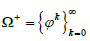 , если эта точка входит в области задания
указанных композиционных степеней.

Композиционные степени ядра имеют различные естественные области задания и области значений, меняющиеся с
изменением степени. Это обстоятельство затрудняет анализ и мы определим новое отображение.
Рассмотрим топологическое вложение

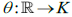 в компакт.
Определение 4. Непрерывное отображение 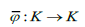 будем называть расширенным ядром, если  для всех 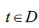 из области задания ядра.
Определение 5. Ядро  на компакт,
2) для каждого непрерывного на  решения уравнения Шрёдера

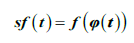
существует непрерывное на компакте решение F уравнения

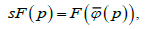
такое что

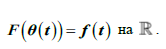
Заметим, что если есть решение компактифицированной задачи, то формула 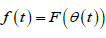 задает непрерывное
решение исходного уравнения Шрёдера, определенное на 

В виду следующей теоремы, нашей целью будет являться поиск условий на ядра, гарантирующие их простоту.
Теорема 1. Уравнение Шрёдера с константой s>1 и простым ядром не имеет нетривиальных непрерывных на
решений.
Доказательство. Рассмотрим компактификацию уравнения Шрёдера. Любое его непрерывное решение F является
ограниченным на компакте 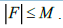 В силу основного уравнения, для любого k и любой точки p компакта K
верна оценка 

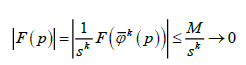
Следовательно, любое решение исходного уравнения, по определению обязанное иметь непрерывное расширение,
с необходимостью тривиально.

Примеры расширенных ядер 

Рассмотрим стереографическую проекцию 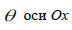 плоскости xOy на окружность  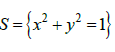без полюса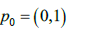  

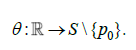
Пусть непрерывное на своей области определения ядро 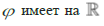 конечное число неустранимых разрывов  . Доопределим ядро в точках устранимых разрывов.
Теорема 2. Если выполнены условия
а) существуют (конечные или бесконечные) пределы  и, если они конечные, то  

б) для любой неустранимой точки разрыва t_k 

где бесконечности могут быть любого знака, то отображение 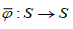 окружности в себя, заданное правилом

является непрерывным в стандартной топологии.

Доказательство. В силу того, что стереографическая проекция и ядро являются непрерывными на своих областях определения, для доказательства непрерывности расширенного ядра достаточно доказать его непрерывность в полюсе и образах точек разрыва.

а) Непрерывность в полюсе. Рассмотрим последовательность точек сходящуюся к полюсу с одной стороны, т.е. лежащие в одной дуге между полюсом и образом нуля. Их стереографическая проекция является последовательностью чисел одного знака стремящейся . Под действием ядра эта последовательность перейдет в сходящуюся последовательность с пределом равным . Таким образом, значение расширенного ядра в полюсе будет равно пределу слева и справа значений ядра спроектированных на окружность.

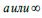
б) Непрерывность в точке  . Аналогично, односторонний предел отобразится на прямой в последовательность, сходящуюся к t_k. Ядро преобразует в последовательность чисел одного знака стремящейся к чьи образы сходятся к полюсу при стереографической проекции.

Достаточные условия простоты ядра

Теорема 3. Если ядро удовлетворяет условиям теоремы 2, т.е. допускает расширение 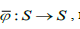 и 

или

б) существует 

то ядро простое.
Доказательство. Достаточно доказать, что любое непрерывное решение уравнения Шрёдера допускает
непрерывное расширение на всю окружность. Композиция 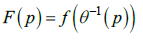 задает непрерывное на всей
окружности, кроме полюса p₀, решение уравнения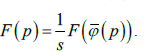  

а) Рассмотрим окрестность U точки 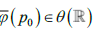  , не содержащей полюс p₀ . По непрерывности расширенного
ядра 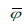 найдется окрестность полюса  образ которой будет содержаться в рассмотренной окрестности 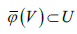 и для всех точек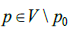  

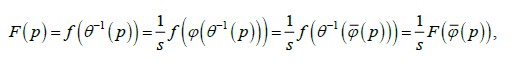
т.е. после доопределения значения функции F в полюсе значением 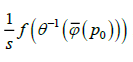  решение F станет
непрерывным отображением также и в полюсе.
б) Это условие означает, что односторонние пределы к точке  под действием расширенного ядра переходят
в односторонние пределы, сходящиеся к полюсу с разных сторон. В силу уравнения Шрёдера, доопределение функции
F в полюсе  задает непрерывную функцию на окружности.

Решение канонических уравнений

Завершение описания гладких общих решений уравнений Бетхера второго порядка [1] состоит в решении пяти оставшихся не решенными канонических уравнений. Они сводятся к пяти семействам уравнений Шрёдера:

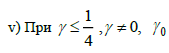 корень уравнения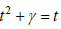 

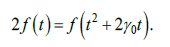
Применим к перечисленным семействам ядер доказанные теоремы.

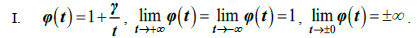 Таким образом, согласно теореме 2 ядро допускает
расширение и согласно теореме 3, пункт б), является простым. Можно применить и пункт а) теоремы 3, т.к.   Непрерывные уравнения Шрёдера тривиальны.

 Аналогично, согласно теореме 2 ядро допускает
расширение и согласно теореме 3, пункт б), является простым. Непрерывные уравнения Шрёдера тривиальны. 

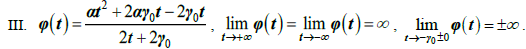 Непрерывные уравнения Шрёдера
тривиальны.

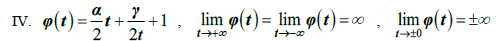 Непрерывные уравнения Шрёдера
тривиальны.

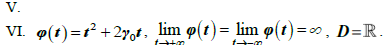 Это ядро допускает расширение, но критерии простоты
не выполнены. В классе непрерывных решений это уравнение остается нерешенным.
Исследование ядра 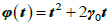 в вещественно-аналитическом случае. 

Теорема 4. Вещественно-аналитическое решение уравнения Шрёдера (v) на прямой с ядром 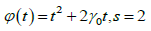 тривиально.
Доказательство. Точка 0t = является неподвижной точкой ядра, следовательно 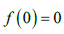 Рассмотрим ряд
Тейлора решения уравнения Шрёдера 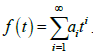 Запишем уравнение

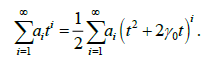
Первое соотношение при сравнении коэффициентов при степенях имеет вид  , которое может дать
ненулевой коэффициент лишь при  является корнем уравнения 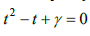 т.е. при  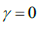 но этот
случай исключен из рассмотрения. Следовательно,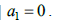  

Если при некоторых ограничениях на 0  все коэффициенты 1, , k a a оказались равными нулю, то уравнение на
коэффициент a_k+1 приобретает вид 

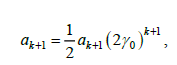
которое влечет 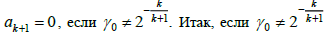 ни при каком k, то ряд тривиален. В частности,
вещественно-аналитическое решение тривиально при условии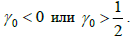  

Рассмотрим условие 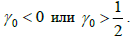  Заметим, что в этом случае 

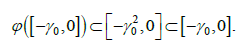
Таким образом, мы получили уравнение Шрёдера на компакте, что влечет тривиальность его непрерывных решений, а в случае вещественной аналитичности тривиальность на промежутке влечет тривиальность решения на всей оси.

Конфликт интересов  Не указан.

Conflict of Interest  None declared.