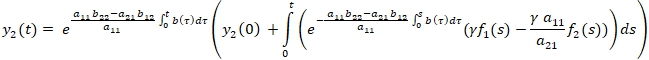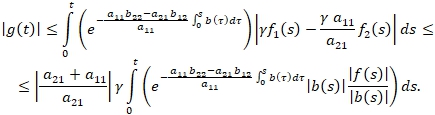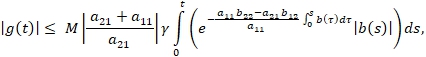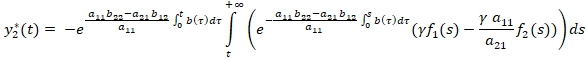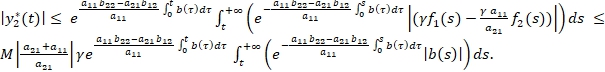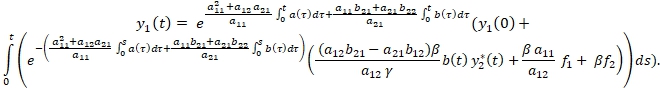О РАЗРЕШИМОСТИ ОДНОЙ СИСТЕМЫ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ПРОСТРАНСТВЕ ОГРАНИЧЕННЫХ НА ВСЕЙ ОСИ ФУНКЦИЙ

О РАЗРЕШИМОСТИ ОДНОЙ СИСТЕМЫ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ПРОСТРАНСТВЕ ОГРАНИЧЕННЫХ НА ВСЕЙ ОСИ ФУНКЦИЙ

Научная статья

Гуломнабиев С.Г. *

ORCIID 0000-0002-5205-0806,

Политехнический институт Таджикского технического университета имени М. Осими, Худжанд. Таджикистан

* Корреспондирующий автор (sardor1967[at]list.ru)

Аннотация

Для одной системы линейных дифференциальных уравнений с неограниченными коэффициентами рассматривается вопрос об однозначной разрешимо-сти в пространстве ограниченных на всей оси функций. При постановке задач матрица коэффициентов разделена на две матрицы, матрица «старших» и матрица «младших» коэффициентов. Предполагается, что спектр матрицы «стар-ших» коэффициентов имеет пересечение с мнимой осью. Выявлены условия для матрицы «младших» коэффициентов, при выполнение которых обеспечивается однозначная разрешимость системы в пространстве ограниченных на всей оси функций. Выявленные условия выписаны с помощью связи между «старшими и младшими» коэффициентами системы.

Ключевые слова: система дифференциальных уравнений, ограниченное на всей оси решение, разрешимость, спектр матрицы, мнимая ось.

ON THE SOLVABILITY OF ONE SYSTEM OF LINEAR DIFFERENTIAL EQUATIONS IN THE SPACE OF FUNCTIONS LIMITED FOR THE ENTIRE AXIS

Research article

Gulomnabiev S.G.*

ORCIID 0000-0002-5205-0806,

Polytechnic Institute of the Tajik Technical University named after Academic M.S.Osimi, Khujand. Tajikistan

Correspondent author (sardor1967[at]list.ru)

Abstract

The issue of unique solvability in the space of functions limited for the entire axis for one system of linear differential equations with unlimited coefficients is considered. When setting tasks, the matrix of coefficients is divided into two matrices, the matrix of “senior” and the matrix of “lower” coefficients. It is assumed that the spectrum of the matrix of “senior” coefficients has an intersection with the imaginary axis. The conditions for the matrix of “lower” coefficients are revealed, the fulfillment of which ensures the unique solvability of the system in the space of functions limited for the entire axis. Revealed conditions are written out using the relationship between the “senior and junior” coefficients of the system.

Keywords: system of differential equations, solution limited for the entire axis, solvability, matrix spectrum, imaginary axis.

Введение В данной статье рассматривается система дифференциальных уравнений

      (1)

где  постоянные квадратные матрицы второго порядка,  - определенные и непрерывные на всей оси функции, удовлетворяющие условиям

     (2) Относительно функции  предполагается также, что они удовлетворяют условию      (3) Для вектор-функции   предполагаем, что имеет место  неравенство      (4)

где 

Ниже рассматривается вопрос о наличии решений системы (1) принадлежащих пространству ограниченных на всей оси функций

Сначала рассмотрим соответствующую однородную систему

     (5)

Общеизвестно, что в силу условия (3) поведение нетривиальных решений однородной системы (5) на бесконечности существенно зависит от расположения спектра матрицы на комплексной плоскости. В случае, когда спектр матрицы А не пересекается с мнимой осью, вышеизложенный вопрос в той или иной форме рассмотрен в многочисленных работах многих математиков [6], [7], [9]. В случае, когда спектр матрицы А пересекается с мнимой осью возникает естественный вопрос: Какими условиями должна обладать матрица В, чтобы можно было гарантировать наличие решений системы (1), принадлежащих пространству ограниченных на всей оси функций

В статье рассмотрен один из простейших возможных вариантов, когда спектр матрицы   пересекается с мнимой осью. А именно предположим, что одно из двух собственных значений матрицы A равно нулю. Если одно (только одно) из собственных значений матрицы A равно нулю, то  Далее предполагается, что для элементов матрицы  А  выполнены условия

   (6) а элементы матрицы В связаны с элементами матрицы А соотношением     (7)

Лемма. Пусть скалярные функции  удовлетворяют условиям (2) и (3), для элементов матрицы A и В выполнены условия (6) и (7), и имеет место  Тогда система (5) не имеет ненулевых решений принадлежащих пространству ограниченных на всей оси функций.

Доказательство. В системе (5) производим замену переменных

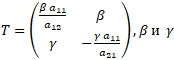    (8) где  произвольные ненулевые числа. 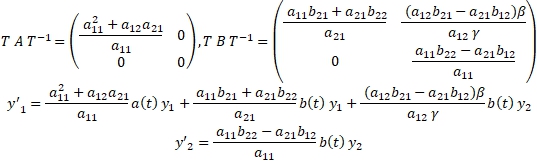После несложных преобразований с учётом (6) и (7) имеем Очевидно, что второе уравнение системы независимое уравнение и допускает представлений решений в явной форме.

В силу условия (2) с учётом  в случае когда  имеем . Следовательно, однородная система не имеет не тривиальных ограниченных на всей оси решений.

Рассмотрим теперь неоднородную систему (1). Не ограничивая общности, для простоты предположим, что   .

Теорема. Пусть выполнены условия леммы. Тогда система (1) для любой функции удовлетворяющей условию (4) имеет единственное решение, принадлежащее пространству ограниченных на всей оси функций.

Доказательство. Произведя замену (7) систему (1) приводим к виду

Общее решение второго уравнения можно задать следующей формулой

Рассмотрим функцию .  Имеем

Из условии (4) следует, что функция  ограниченна на всей оси т.е. существует число М, такое, что . С учетом последнего неравенство имеем

В силу условия  имеем 

Пусть  Случай  рассматривается аналогично. Подобрав соответствующим образом значение    рассмотрим частное решение второго независимого уравнения

Для оценки  имеем

Используя правило Лопиталя с учетом условия (4), легко доказать, что  функция  ограничена на всей оси, т.е. существует N, такое что . Теперь подставляя  в первое уравнение, получим

Запишем общее решение в форме

Предположим, что   Из условия (3) следует, что  где  Тогда  Следовательно, начиная с некоторого достаточно большого значения t знак выражения, стоящий перед  совпадает со знаком выражения

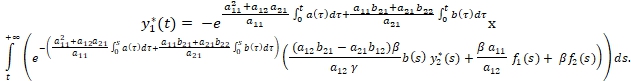Рассмотрим частное решение Оценим отдельно подынтегральное выражение Имеем для оценки 

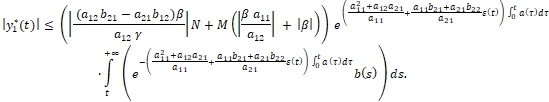
Пользуясь правилом Лопиталя, как и прежде, легко можно вывести ограниченность функции  Следовательно,  является единственным ограниченным решением системы (9). Единственность решения следует из леммы. Тогда  является единственным ограниченным решением системы (1).

Теорема доказана.

Конфликт интересов	Conflict of Interest
Не указан.	None declared.

Список литературы / References

1. Крейн М. Г. Лекции по теории устойчивости решений дифференциальных уравнений в банаховом пространстве / М. Г. Крейн. – Киев, 1964.
2. ДемидовичБ.П. Лекции по математической теории устойчивости / Б.П. Демидович. – М.: Наука, 1967.
3. Далецкий Ю. Л. Устойчивость решений дифференциальных уравнений в банаховом пространстве / Ю.Л. Далецкий, М. Г. Крейн. – М.: Наука, 1970.
4. МухамадиевЭ.М. Об обратимости дифференциальных операторов в пространстве непрерывных и ограниченных на оси функций / Э.М. Мухамадиев // ДАН СССР, 1971. – Т. 196, № 1. – С. 47-49.
5. ГантмахерФ.Р. Теория матриц / Ф.Р Гантмахер. – М.: Наука, 1980.
6. Лабиб Р. О существовании ограниченных решений системы линейных дифференциальных уравнений с неограниченными коэффициентами / Р. Лабиб. // ДАН Тадж.ССР, 1989. – Т. 32, № 1. – С. 425-427.
7. Байзаев С. Ограниченные решения некоторых обыкновенных дифференциальных уравнений в банаховом пространстве / С. Байзаев, Э. Мухамадиев // Вестник ТГУПБП. – №1(41). – 2010. – С. 108-112.
8. Зиёмидинов Б.М. Предельные решения и условие разрешимости систем дифференциальных уравнений первого порядка в пространствах Степанова / Б.М. Зиёмидинов, С.Г. Гуломнабиев // Доклады Академии наук Республики Таджикистан. – 2015. – Т. 58.№9. –С. 780-785.
9. Гуломнабиев С.Г. О решениях однородной системы линейных дифференциальных уравнений в пространствах суммируемых функций / С.Г. Гуломнабиев // Вестник Таджикского национального университета. Серия естественных наук. – 2019. – №2. – С. 91-95.
10. Гуломнабиев С.Г. О некоторых свойствах решений линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами / С.Г. Гуломнабиев // Актуальные вопросы дифференциальных  уравнений, математического  анализа,  алгебры  и  теории  чисел  и  их приложения:  материалы  Республиканской  научно-практической конференции. – Душанбе: РТСУ, 2019. – С 78-82.

Список литературы на английском языке / References in English

1. Krejn M. G. Lekcii po teorii ustojchivosti reshenij differencial'nyh uravnenij v banahovom prostranstve [Lectures on the theory of stability of solutions of differential equa-tions in a Banach space] / M. G. Krejn. – Kiev, 1964. [in Russian]
2. Demidovich B.P. Lekcii po matematicheskoj teorii ustojchivosti [Lectures on the mathematical theory of stability] / B.P. Demidovich. – M.: Nauka, 1967. [in Russian]
3. Daleckij Ju. L. Ustojchivost' reshenij differencial'nyh uravnenij v banahovom prostranstve [Stability of solutions of differential equations in a Banach space] / Ju.L. Daleckij, M. G. Krejn. – M.: Nauka, 1970. [in Russian]
4. Muhamadiev Je.M. Ob obratimosti differencial'nyh operatorov v prostranstve nepreryvnyh i ogranichennyh na osi funkcij [On the invertibility of differential operators in the space of continuous and axis-bounded functions] / Je.M. Muhamadiev // DAN SSSR, 1971. – V. 196, № 1. – P. 47-49. [in Russian]
5. Gantmaher F.R. Teorija matric [Matrix theory] / F.R Gantmaher. – M.: Nauka, 1980. [in Russian]
6. Labib R. O sushhestvovanii ogranichennyh reshenij sistemy linejnyh differencial'nyh uravnenij s neogranichennymi kojefficientami [On the existence of bounded solutions of systems of linear dif-ferential equations with unbounded coefficients] / R. Labib. // DAN Tadzh. SSR, 1989. – V. 32, № 1. – P. 425-427. [in Russian]
7. Bajzaev S. Ogranichennye reshenija nekotoryh obyknovennyh differencial'nyh uravnenij v banahovom prostranstve [Bounded solutions of some ordinary differential equations in a Banach space] / S. Bajzaev, Je. Muhamadiev // Vestnik TGUPBP [Bulletin of TGUPBP]. – №1(41). – 2010. – P. 108-112. [in Russian]
8. Zijomidinov B.M. Predel'nye reshenija i uslovie razreshimosti sistem differencial'nyh uravnenij pervogo porjadka v prostranstvah Stepanova [Limit solutions and the solvability con-dition for systems of first-order differential equations in Stepanov spaces] / B.M. Zijomidinov, S.G. Gulomnabiev // Doklady Akademii nauk Respubliki Tadzhikistan [Reports of the Academy of Sciences of the Republic of Tajikistan]. – 2015. – V. 58. № 9. –P. 780-785. [in Russian]
9. Gulomnabiev S.G. O reshenijah odnorodnoj sistemy linejnyh differencial'nyh uravnenij v prostranstvah summiruemyh funkcij [On solutions of a homogeneous system of linear differential equations in spaces of summable functions] / S.G. Gulomnabiev // Vestnik Tadzhikskogo nacional'nogo universiteta. Serija estestvennyh nauk. [Bulletin of the Tajik National Uni-versity. A series of natural sciences] – 2019. – № 2. – P. 91-95. [in Russian]
10. Gulomnabiev S.G. O nekotoryh svojstvah reshenij linejnyh odnorodnyh differencial'nyh uravnenij vtorogo porjadka s postojannymi kojefficientami [On some properties of solutions of linear homogeneous second-order differential equations with constant coefficients] / S.G. Gulomnabiev // Aktual'nye voprosy differencial'nyh uravnenij, matematicheskogo analiza, algebry i teorii chisel i ih prilozhenija: materialy Respublikanskoj nauchno-prakticheskoj konferencii [Actual problems of differential equations, mathematical analysis, algebra and number theory and their applications: materials of the Republican scientific and practical con-ference]. – Dushanbe: RTSU, 2019. – P. 78-82 [in Russian]