МЕЖДИСЦИПЛИНАРНОЕ ОБРАЗОВАНИЕ: ОБУЧЕНИЕ МАТЕМАТИКЕ С ИСПОЛЬЗОВАНИЕМ КОМПЬЮТЕРНЫХ МАТЕМАТИЧЕСКИХ ПАКЕТОВ В СИСТЕМЕ ПОДГОТОВКИ БУДУЩИХ БАКАЛАВРОВ И МАГИСТРОВ НЕМАТЕМАТИЧЕСКИХ НАПРАВЛЕНИЙ В УСЛОВИЯХ ИНФОРМАТИЗАЦИИ

МЕЖДИСЦИПЛИНАРНОЕ ОБРАЗОВАНИЕ: ОБУЧЕНИЕ МАТЕМАТИКЕ С ИСПОЛЬЗОВАНИЕМ КОМПЬЮТЕРНЫХ МАТЕМАТИЧЕСКИХ ПАКЕТОВ В СИСТЕМЕ ПОДГОТОВКИ БУДУЩИХ БАКАЛАВРОВ И МАГИСТРОВ НЕМАТЕМАТИЧЕСКИХ НАПРАВЛЕНИЙ В УСЛОВИЯХ ИНФОРМАТИЗАЦИИ

Научная статья

Горлов C. И.¹, Казиахмедов Т. Б.^2, *

^{1, 2} Нижневартовский Государственный Университет, Нижневартовск, Россия

* Корреспондирующий автор (ktofik[at]yandex.ru)

Аннотация

Появившиеся новые возможности повышения качества математической подготовки выше бакалавров и магистров нематематических направлений подготовки в связи с появлением богатейших инструментов вычислительной и символьной математики, к сожалению, не используются. Мы, как и прежде считаем: будет математическое мышление -будут и знания. Но математическое мышление развивается в ходе решения профессиональных вычислительных задач. Использование математических методов в различных сферах профессиональной деятельности в условиях внедрения информационных технологий во все сферы человеческой деятельности требует пересмотра методов обучения, содержания математической подготовки, изучения инструментария вычислительных методов и математического моделирования.

В данной статье рассматриваются инновационные подходы в математической подготовке бакалавров и магистров нематематических направлений, связанные с использованием математики как инструмента решения профессиональных задач.

Ключевые слова. Вычислительный эксперимент как инструмент обучения, вычислительная наука, новые дисциплины на межпредметной основе, пакеты математических вычислений и моделирования, профессионально ориентированная методика обучения математике, психологические особенности формирования культуры математических вычислений.

INTERDISCIPLINARY EDUCATION: TEACHING MATHEMATICS WITH COMPUTER MATHEMATICAL PACKAGES IN PREPARING BACHELORS AND MASTERS OF NON-MATHEMATICAL DIRECTIONS UNDER CONDITIONS OF INFORMATIZATION

Research article

Gorlov C. I.¹, Kaziahmedov T. B.^2, *

^{1, 2} Nizhnevartovsk State University, Nizhnevartovsk, Russia

* Corresponding author (ktofik[at]yandex.ru)

Abstract

Several new opportunities to improve the quality of mathematical training of bachelors and masters in non-mathematical areas connected with the appearing of the wealthiest tools of computational and symbolic mathematics, unfortunately, are not currently used. Just like before, we believe that when there is mathematical thinking, there is knowledge. But mathematical thinking is developed in the course of solving professional computational problems. The use of mathematical methods in various fields of professional activity in the context of the introduction of information technology in all spheres of human activity requires a review of teaching methods, the content of mathematical training, the study of tools of computational methods and mathematical modeling.

This paper discusses innovative approaches in the mathematical preparation of bachelors and masters in non-mathematical areas, associated with the use of mathematics as a tool for solving professional problems.

Keywords: A computational experiment as a teaching tool, computational science, new disciplines on an interdisciplinary basis, packages of mathematical calculations and modeling, a professionally-oriented methodology for teaching mathematics, psychological features of the formation of a culture of mathematical calculations.

Введение

В век информатизации и возникновения множества вычислительных пакетов и пакетов математического моделирования требуется изменение, как содержания, так и методических подходов обучения математике. Такой вывод основан на многолетних наблюдениях отношения к математике бакалавров на выпуске из вуза и непосредственно после их трудоустройства и в ходе работы. Анализировались следующие параметры: математические дисциплины в планах бакалавриата и магистратуры, математические методы в области будущей профессии, качество математических знаний, понимание выпускником необходимости использования компьютерных математических пакетов.

В начале информатизации предполагалось, что наконец-то математика станет не только уделом избранных, но и широких слоев профессионального сообщества. Очевидно, что нет какой-либо области профессиональной деятельности, где можно обойтись без математических методов анализа и измерений (вычислений). Но, тем не менее, большинство выпускников вузов нематематических направлений не видят в своей профессиональной деятельности значимость математических знаний. Это, прежде всего потому, что сам наш подход обучения математике способствует такому видению роли математики. Во-первых, мы по инерции и с уменьшением количества реальных часов на обучение математике, стараемся дать им весь инвариант науки с охватом как можно большого количества разделов без привязки к будущей профессиональной деятельности. Потом за счет курсов по выбору хотим научить математическим методам и компьютерным математическим пакетам. При этом сталкиваемся с тем, что математику они почему-то не освоили. Приведем наши наблюдения и результаты ответов на некоторые наши вопросы выпускникам на выходе и на рабочих местах.

“Подход, ориентированный на изучение инварианта математики как общего курса и потом адаптации математики к профессиональной области не всегда себя оправдывает именно при подготовке бакалавров и магистров нематематических направлений” [3].

Мы целью исследования ставили определение факторов, способствующих изменению отношения к математике как к инструментарию решения профессиональных задач

Аналогично тому, как информационные технологии коренным образом изменили существующие десятилетиями профессии в экономической сфере, так точно они способствуют изменению преподаваемых в вузах дисциплин в сторону межпредметности особенно в области изучения математики бакалаврами и магистрами нематематических направлений подготовки. Таким образом, нужно определить новые содержательные и методические подходы для формирования знаний из области математики для использования в профессиональной деятельности.

Методы и принципы исследования

В ходе исследования рассматривались такие параметры: успеваемость по математике, понимание необходимости математических знаний в профессиональной сфере. Использовались такие методы как анализ, анкетирование, практическое тестирование умений использования математических пакетов в решении задач.

В последние годы в высшем образовании в России в нематематических профилях подготовки формой контроля выступает зачет, поэтому мы рассматривали те направления, где по математике сдается экзамен или дифференцированный зачет. Результаты успеваемости представлены в следующей таблице.

 

Таблица 1 – Примерная успеваемость выпускников по математике

Факультет	Количество студентов	Оценки “4” и 5”	Оценка “3”
Гуманитарный факультет	30	4	26
Педагогики и психологии	40	22	18
Художественно-графический факультет	20	11	9
Физкультурный факультет	30	6	24
Экономический факультет	40	14	26
Итого:	160	57	103

 

Этим же студентам были предложены ответить на вопросы:

Нужна ли Вам математика в будущей профессиональной деятельности? (Если да, то, какие именно разделы математики)

Знакомы ли Вы с математическими пакетами компьютерных вычислений? (Если да, то перечислите их)

Знакомы ли вы с компьютерными программами предназначенными только для вашей профессиональной деятельности? (Перечислите)

 

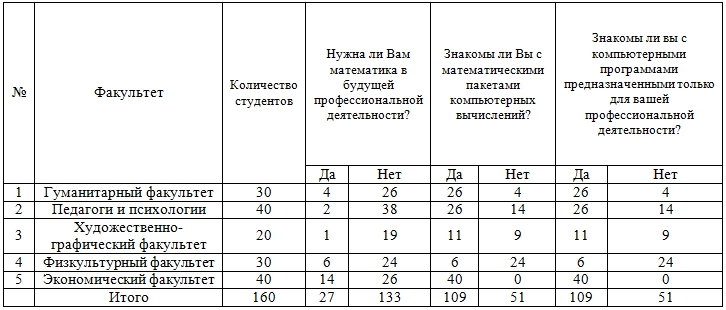
Таблица 2 – Результаты опроса студентов

Что касается последнего вопроса, то студенты перечисляли в основном офисные технологии, которых они изучили в курсе дисциплины “Информатика” или “Информационные технологии” за исключением студентов экономических направлений. Они отметили важность знания разных модулей пакета 1С. Пакеты математических вычислений им мало известны. Этот вопрос наводит нас на мысль, что не существует подхода обучения математике основываясь на возможности этих пакетов с ориентацией на область профессиональной деятельности.

Повышение качества обучения математике –это проблема, изучаемая как в школьном, так и вузовском образовании [4], [5], [6]

Происходящие изменения в объеме учебной нагрузки в сторону сокращения по математическим дисциплинам для бакалавров нематематических профилей воспринимается преподавателями с непониманием. Недовольство строится на таком понимании: чтобы вычислять и моделировать нужно, владеть математическим мышлением [7].

Необходимо четко определить какая математическая подготовка является актуальной для данного направления, и какие вычислительные инструменты они должны знать. Мы приходим к выводу, что в этих направлениях от задачи формирования математического мышления нужно переходить к практике математических вычислений и моделирования, при этом в понятие вычислительной науки включить такие разделы как теория вероятностей и математическая статистика, вычислительная математика (Численные методы для математиков), методы оптимальных решений (Методы оптимизации для математиков), вычислительная геометрия, теория управления, математические методы в предметной области (например, математические методы в экономике, социологии, психологии и т.д.). Нам кажется, что инвариант математики нужно изучать в ходе изучения дисциплины на межпредметной основе, к примеру “Математические методы в профессиональной деятельности”.

Западные ученые в последнее время выделяют в отдельную предметную область вычислительную науку. Не станем исследовать обоснованность такого подхода, но нам нужно иметь в виду, что математиками и программистами разработаны богатейшие компьютерные пакеты вычислительных программ. Если понимать под вычислительной наукой собственно вычислительные математические методы и совокупность разработанных вычислительных инструментов, то мы не видим здесь противоречия. Так, например, в 2005 году консультативный комитет по информационным технологиям при президенте США представил аналитический доклад именно по этой проблеме. В докладе содержатся результаты анализа состояния дел по развитию информатики в США и показано, что здесь необходимо принимать решительные действия на федеральном уровне для предотвращения тех негативных тенденций, которые в настоящее время наблюдаются и в американской науке, и в системе образования. В докладе показано, что развитие «вычислительной науки» создаёт сегодня уникальные возможности для проведения научных исследований [1]. Мы хотим только добавить, что существующие компьютерные математические пакеты носят в себе уникальные дидактические инструменты повышения качества математического образования.

Что же касается собственно вычислительных аспектов информатики, то им в России всегда уделялось значительное внимание. При этом сформировалось научное направление, которое уже более 35 лет активно развивается российскими учеными и получило в нашей стране название вычислительного эксперимента. Основоположником этого направления является академик А.А. Самарский.

Вычислительный эксперимент — метод изучения устройств или физических процессов с помощью математического моделирования. Он предполагает, что вслед за построением математической модели проводится ее численное исследование, позволяющее «проиграть» поведение исследуемого объекта в различных условиях или в различных модификациях [2].

Таким образом, информационные технологии должны способствовать использованию математического аппарата во всех сферах экономической деятельности, где необходимы вычисления и математическая оценка различных параметров хозяйствования. Прежде всего отметим, что математические пакеты способствуют формализованному восприятию формальной структуры задачи, формированию логического мышления в сфере количественных и пространственных отношений, математической памяти, культуры математических вычислений.

Математические пакеты позволяют визуализировать основные понятия и на уровне изучения даже строить эксперименты, определяющие поведенческую сущность функций, предикатов, методов.

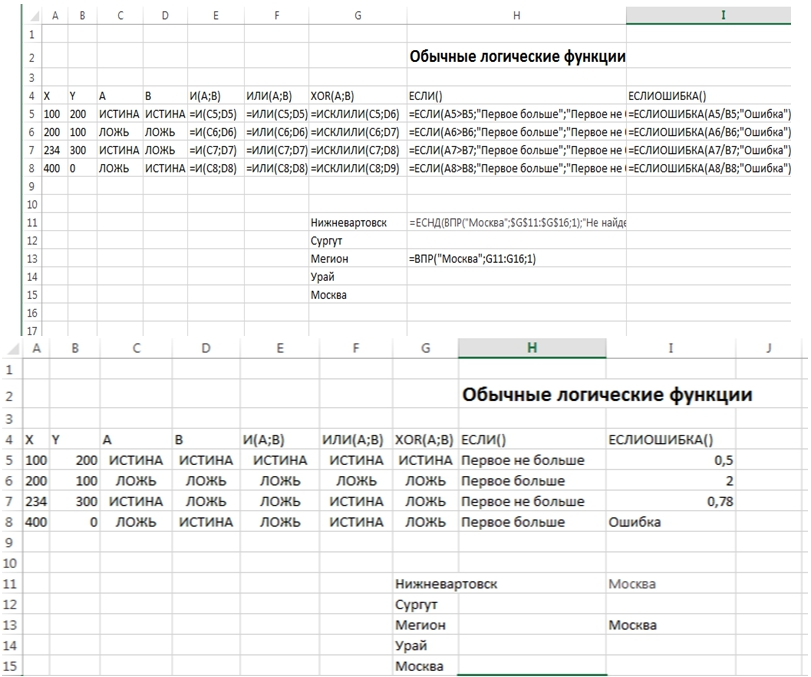
Например, при изучении основ математической логики математические пакеты позволяют не только усвоить и запомнить основные функции, но и апробировать их в действии меняя значения параметров. На рисунке 1 демонстрируются логические функции в EXCEL.

 

Рис. 1 – Пример использования логических функций

 

Причем, эти функции используется в простейших задачах профессиональной области.

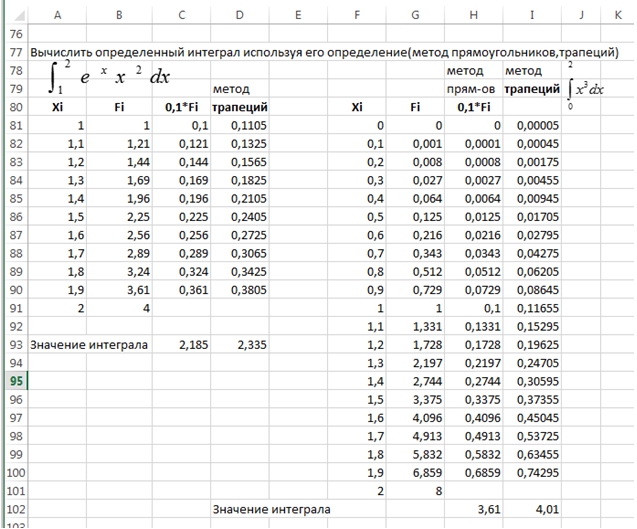
Очень важную роль играют математические пакеты программ в формировании способности к логическому мышлению. Рассмотрим простейшие таблицы вычисления определенного интеграла.

Рис. 2 – Вычисление определенного интеграла разными методами

 

Более подробно использование EXCEL как инструмента формирования качественных математических знаний и умений можно ознакомиться в [3].

Приведение профессиональных задач к задачам функционального анализа, матричной алгебры, вычислительным задачам, задачам статистики и геометрии - это очень важная, но и самая сложная часть формирования качества математических компетенций в профессиональной деятельности бакалавров и магистров гуманитарных направлений.

Попытки изучить эти разделы собственно в предмете “Математика”, а потом демонстрировать, что вот, мол, математика - это серьезный инструмент для вашей профессии не приносит желаемых результатов.

 

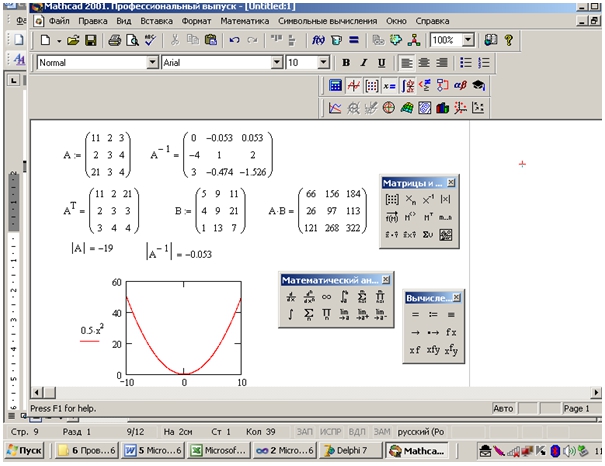
Рис. 3 – Использование среды MathCad как инструмента формирования математических знаний

Как было отмечено выше, использование математических пакетов в задачах матричной алгебры, математического анализа, вычислительной математики, математической логики, для изучения поведения функций, описывающих проблематику профессиональной деятельности, способствует не только пониманию логики методов и операций, но и формированию математической памяти, культуры вычислений или культуры использования математических пакетов в профессиональных задачах. Таким образом, последовательность изучения дисциплин на межпредметной основе предлагаемая нами такова:

• задачи профессиональной деятельности, решение которых требует использование инструментария математики;
• изучение инструментария с соответствующими объяснениями преподавателя;
• решение и анализ задачи;
• изучение инварианта раздела математики.

Причем, на последний шаг нужно отводить больше заданий самостоятельного изучения. (Например, изучите раздел “Матричные методы решения систем линейных уравнений”). Готовьте презентацию и доклад к семинару. В докладе выделите классы задач из профессиональной области, решения которых основаны на знаниях из этого раздела).

Математические пакеты очень удобны в организации учебных исследовательских экспериментов в получении различных состояний объектов из профессиональной деятельности при изменении параметров в математической модели. Такие занятия исследовательского характера способствуют формированию математического мышления, математической памяти благодаря возможности визуализации вычислений и их результатов.

Хотим отметить, что даже отсутствие высоко профессиональных и дорогих математических компьютерных пакетов не является проблемой для знакомства бакалавров нематематических профилей с вычислительными экспериментами в задачах из профессиональной деятельности.

Во-первых, во всех образовательных учреждениях используются электронная таблица Microsoft EXCEL.Этот программный продукт является уникальным инструментом для изучения основ математической логики, теории вероятностей, математической статистики, некоторых разделов математического анализа, матричной алгебры, вычислительной математики, основ математического моделирования бакалаврами нематематических специальностей.

Во-вторых, сегодня имеется множество бесплатных программных продуктов, таких как EULER, SciLab .

Приведем формулировку некоторых типов заданий:

Выделите задачи из профессиональной области, решаемые с использованием алгебры. Вычислить сумму, произведение двух матриц. Найти обратную матрицу. Решить систему линейных уравнений. Проверить свои решения в EXCEL(MathCad, EULER, SciLab).

Выделите задачи из профессиональной области, решаемые с использованием знаний из области математического анализа. Вычислить производные, определенные интегралы методами прямоугольников, трапеций, касательных и проверить свои решения в EXCEL(MathCad, EULER, SciLab ).

Решите задачу линейного программирования, транспортную задачу и выполнить проверку средствами компьютерных математических пакетов.

Определите характеристики случайных процессов и моделируйте в среде EXCEL(СТАТИСТИКА).

Решите задачи прогнозирования изменения каких-либо процессов из своей профессиональной деятельности (простудные заболевания, динамика роста числа абитуриентов, рост количества покупаемых автомобилей населением вашего города, динамика роста населения вашем городе, регионе) и анализируйте свои модели и решения средствами статистических функций EXCEL, Статистика.

Постройте различные предикаты, используя базовые простые функции. Проверяйте в EXCEL верность ваших преобразований.

Используя все группы функций, моделируйте различные игры из профессиональной области.

Результаты.

Надо было на практике исследовать, как сочетать инструментальные средства математических вычислений и инвариант математики, чтобы достичь поставленной цели. Было решено, преподавать следующие межпредметные учебные дисциплины:

Математическая статистика в среде EXCEL;

Линейная алгебра и решение профессиональных задач в среде MathCad;

Сопровождение педагогического эксперимента инструментами среды EXCEL и другие.

Причем, в некоторых группах эти дисциплины изучались параллельно с изучением математики. А в группах, в которых изучение этих дисциплин не было сопряжено с изучением математики, преподаватель сам давал необходимые базовые знания. Главной задачей было определение изменения отношения к математике как к инструменту решения профессиональных задач, и собственно динамика изменения качества успеваемости по математике.

Результаты для нас были неожиданными. Качество успеваемости при такой же выборке студентов возросло до 80%. Практически 90 % студентов отметили необходимость математических знаний. Для согласования данных дисциплин с Федеральным государственным стандартом РФ (ФГОС 3+) перечисленные выше курсы были организованы в последствии как курсы по выбору, причем эти курсы были объявлены на разных профилях нематематических направлений. Интерес к этим курсам велик. Так, на дисциплину “Математическая статистика в среде EXCEL” записались 160 студентов 3 курса перечисленных в таблице №1 направлений, при их общей численности 217 человек.

Обсуждение

Использование бесплатных пакетов EULER(Эйлер), SciLab (СайЛАБ), Free Math, EXCEL позволяет преподавателю колоссальные возможности для формирования культуры компьютерных вычислений.

Качество математического образования меняется в лучшую сторону, когда мы строим обучение математике через решение задач из профессиональной области с использованием математических компьютерных пакетов и в этом процессе углубляемся в инвариант математики.

Обучение математике в средней школе, средних специальных учебных заведениях(ссузе), вузе через задачи, ориентированные на профессии региона показало право на существование. Долгое время в практике школ учителями математики использовались дополнительно сборники задач, ориентированных на профессии в регионе[4]. Не богат опыт в практике вузов использования современных компьютерных математических пакетов для решения задач из профессиональной области.

Наш опыт разработки и внедрения курсов на междисциплинарной основе в систему подготовки бакалавров и магистров нематематических направлений привел нас к кадровой проблеме. Ведь не всегда математики знают другие предметные области, и знатоки предметной области владеют аппаратом математики.

Поэтому коренным образом изменить подготовку предметников, т.е. преподавателей, ведущих профессиональные дисциплины по направлению подготовки, расширить их кругозор и знания в области использования математики в профессиональной сфере. Мы думаем, что нет противоречия в том, что одну дисциплину будут вести 2-3 преподавателя. А со временем эта проблема решится сама благодаря подготовке новых преподавательских кадров, владеющих математическим инструментарием (вычислительной наукой) в своей профессиональной деятельности.

Заключение. Переход на междисциплинарное обучение ставит перед вузовским образованием колоссальную задачу - сформировать новые учебные дисциплины на многопредметной основе, причем определяющим здесь ориентиром формирования учебных дисциплин является профессиональная область. Остаются вне поле нашего исследования инженерные и математические направления подготовки.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Колин К.К. Будущее информатики в 21 веке: российский ответ на американский вызов. // Открытое образование, № 2(55), 2006. – С. 73-77.
2. Самарский А.А.Математическое моделирование и вычислительный эксперимент // Вестник АН СССР. — 1979. — №5. — С. 38–49.
3. Горлов С.И. Компьютерные математические пакеты в системе подготовки будущих бакалавров и магистров нематематических направлений в условиях информатизации / С.И. Горлов, Т.Б. Казиахмедов // Педагогическая информатика,№4, 2016. С. 50-59
4. Абрамов А. В.Математика впрофессиях Тюменского Севера: Сб. задач: Пособие для учителей математики средних школ Тюменской области / А. В. Абрамов, О.Б Епишева, Т.Б. Казиахмедов и др. / Под ред. А.В. Абрамова. – Екатеринбург: Изд-во Урал. Ун-та; Нижневартовск: Изд-во Нижневартовского пед. ин-та, 1993. – 112с.
5. Колмогоров А.Н. Математика –наука и профессия. –М.: Наука. Главная редакция физико-математической литературы, 1988. -289 с.
6. Дорофеев А.В. Проектирование математической учебной деятельности в профессиональном образовании будущего педагога. Образование и наука, №2, 2005. ,С. 82-90
7. Вейль Г. Математическое мышление. Пер. с англ. и нем./Под ред. Б.В. Бирюкова и А.Н. Паршина.-М.: Наука. Главная редакция физико-математической литературы,1989. -400 с.

Список литературы на английском языке / References in English

1. Colin K.K. Budushcheye informatiki v 21 veke: rossiyskiy otvet na amerikanskiy vyzov [Future of computer science in 21st century: Russian response to American challenge] // Otkrytoye obrazovaniye [Open education]. – No. 2 (55). – 2006. – P. 73-77. [in Russian]
2. Samarsky A.A. Matematicheskoye modelirovaniye i vychislitel'nyy eksperiment [Mathematical modeling and computational experiment] // Vestnik AN SSSR [Bulletin of the USSR Academy of Sciences]. – 1979. – No. 5. – P. 38–49. [in Russian]
3. Gorlov S. I. Komp'yuternyye matematicheskiye pakety v sisteme podgotovki budushchikh bakalavrov i magistrov nematematicheskikh napravleniy v usloviyakh informatizatsii [Computer mathematical packages in training system for future bachelors and masters in non-mathematical areas in context of informatization] / S. I. Gorlov, T. B Kaziakhmedov // Pedagogicheskaya informatika [Pedagogical informatics] – No. 4. – 2016. – P. 50-59 [in Russian]
4. Abramov A.V. Matematika v professiyakh Tyumenskogo Severa [Mathematics in professions of Tyumen North] / A.V. Abramov, O.B. Episheva, T.B. Kaziakhmedov and others. // Coll of problems: A manual for mathematics teachers of secondary schools of the Tyumen region / Ed. by A.V. Abramova. – Yekaterinburg: Publishing House Ural. University; Nizhnevartovsk: Publishing house of Nizhnevartovsk ped. in-that, 1993. – 112 p. [in Russian]
5. Kolmogorov A.N. Matematika – nauka i professiya [Mathematics is science and profession]. – M.: Science. Main edition of physical and mathematical literature, 1988. – 289 p. [in Russian]
6. Dorofeev A.V. Proyektirovaniye matematicheskoy uchebnoy deyatel'nosti v professional'nom obrazovanii budushchego pedagoga [Designing mathematical training activities in vocational education of future teacher] / Obrazovaniye i nauka [Education and science]. – No. 2, – 2005, p. 82-90 [in Russian]
7. Weil G. Matematicheskoye myshleniye [Mathematical thinking] / Trans. from English and German. / Ed. by B.V. Biryukova and A.N. Parshina. –M.: Science. Main edition of the physical and mathematical literature, 1989. – 400 p. [in Russian]