ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ТЕПЛОМАССООБМЕНА СЖИЖЕННОГО ПРИРОДНОГО ГАЗА В ГОФРИРОВАННОМ КРИОБАКЕ

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ТЕПЛОМАССООБМЕНА СЖИЖЕННОГО ПРИРОДНОГО ГАЗА В ГОФРИРОВАННОМ КРИОБАКЕ

Научная статья

Вдовичев А.А.^{1, *}

¹ Санкт-Петербургский государственный архитектурно-строительный университет, Санкт-Петербург, Россия;

¹ ORCID: 0000-0001-8979-8845,

* Корреспондирующий автор (fansw[at]bk.ru)

Аннотация

В статье рассматривается перспективная модель топливного СПГ-бака, позволяющая увеличить время бездренажного хранения за счет обеспечения постоянной степени заполнения изотермического сосуда жидкой фазой топлива. Выполнено технологическое описания способа поддержания неизменяемой объемной доли криогенного топлива в сжиженном состоянии путем использования гофрированной конструкции сосуда по типу сильфонного осевого компенсатора. Осуществлена постановка задачи программного расчета с использованием метода конечных объемов, позволяющего описать распределение физических параметров двухфазной системы «жидкость-газ» с учетом наличия теплопритока к стенкам рассматриваемого гофрированного сосуда. Приведены результаты численного эксперимента бездренажного хранения криожидкости без стравливания продукта в систему питания двигателя внутреннего сгорания, выявлены недостатки аналитического исследования процессов тепломассопереноса и гидродинамики СПГ в криогенной изотермической емкости.

Ключевые слова: сжиженный природный газ, топливный криогенный бак, бездренажное хранение, тепломассообмен, свободно-конвективное движение, моделирование гидродинамического поля бинарной системы.

Введение

Одной из наиболее актуальных проблем для автомобилей, работающих на сжиженном природном газе (СПГ), является увеличение времени удержания криогенного продукта без стравливания его в атмосферу. Данная проблема особенно важна для транспортных средств, осуществляющих длительную поездку с регламентом работы, требующим периодические остановки, например, магистральных тягачах или спецтехнике [1, С. 70].

Как известно, при хранении и транспортировке СПГ в изотермических топливных баках происходит непрекращающийся процесс испарения жидкой фазы за счет имеющегося температурного напора через стенки сосуда, что, в свою очередь, является причиной повышения избыточного давления   образующихся паров природного газа и ведет к снижению времени бездренажного хранения криопродукта.

В настоящее время имеется несколько способов утилизации выпара. Например, на крупных танкерах применяются системы принудительного сжижения газообразного СПГ – холодильные машины, работающие по циклу Стирлинга [2, С. 168]. Однако использование таких установок для конденсации паров в автотранспортных средствах является экономически нецелесообразным. Зачастую для увеличения времени удержания сжиженного газа в автомобилях применяются следующие технические способы. Во-первых, с целью снижения теплопереноса через конструкцию топливного бака в межстенном пространстве криогенного сосуда располагают высокоэффективную экранно-вакуумную теплоизоляцию, обладающую сверхнизким коэффициентом теплопроводности [3, С. 25-28]. Во-вторых, используется система подачи газообразного топлива в двигатель в том случае, когда давление в сосуде становится выше верхней границы рабочего давления [4]. Тем не менее, ни одним из существующих технологических решений не предусмотрено поддержание постоянной начальной степени заполнения жидкой фазы криопродукта φ₀.

Степень заполнения жидкой фазы криопродукта оказывает непосредственное влияние на интенсивность процесса испарения и, следовательно, величину избыточного давления в герметичном объеме криобака. В случае полного заполнения сосуда СПГ, без наличия парового пространства, при переносе теплоты внутрь емкости происходит резкое повышение избыточного давления и, как следствие, стравливание газа в атмосферу через систему аварийного сброса [5, С. 545-546]. При частичном заполнении криобака создаются условия для увеличения интенсивности испарения топлива по причине перехода кинетической энергии жидкости в тепло, вызванное толчками и трением сжиженного газа о стенки сосуда при движении транспортного средства [6, С. 103]. В зависимости от вида криогенного топлива, значения избыточного давления и объема бака существует оптимальная степень заполнения жидкой фазы, при которой период бездренажного хранения максимален. Установлено, что для сжиженного природного газа при рабочем давлении 0,4 МПа она составляет 75% (с учетом особенностей конструкции криобака), что позволяет продлить срок хранения СПГ до 9-10 дней [7].

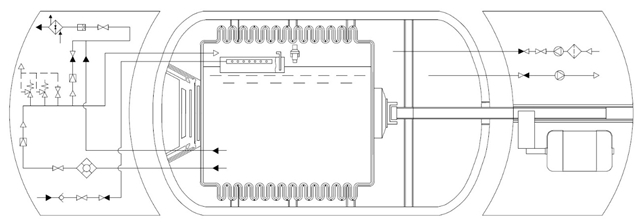
Разработанная перспективная модель криогенного топливного бака с изменяющимся объемом позволяет увеличить время бездренажного хранения СПГ (см. рисунок 1). Способ ее работы основан на принудительном изменении объема конструкции путем сдвига упругой гофрированной металлической оболочки, представляющей собой осевой сильфонный компенсатор, заглушенные основания которого образуют герметичное пространство. Осевое перемещение торцов конструкции позволяет поддерживать неизменяемость отношения геометрического объема жидкого метана V₀ к объему емкости V_p. Тем самым решается проблема уменьшения начальной степени заполнения φ₀ в ходе забора криотоплива в двигатель.

Работа системы поддержания статичного положения зеркала жидкости относительно дна сосуда основана на том, что при излучении измерителем уровня СПГ ультразвуковой волны, отражающейся от свободной поверхности раздела  «газ-жидкость», осуществляется подача сигнала на электродвигатель, в результате чего выполняется вращательно-поступательное движение штока. Оно передается поршню, оказывающему давление на основание стенки сосуда-компенсатора. Таким образом, в условиях, когда часть жидкого СПГ была стравлена в ДВС, возникающее осевое сжатие гибкой мембраны приводит к уменьшению внутреннего объема емкости и обеспечению постоянства объемной доли жидкой фазы криопродукта.

Рис. 1 – Принципиальная схема системы локального хранения сжиженного природного газа с изменяющимся объемом

Разработка перспективной модели СПГ-бака на первичном этапе требует предварительных исследований связанных с изучением гидродинамики и тепломассообмена в условиях хранения криопродукта в замкнутом пространстве гофрированного изотермического сосуда.

Теоретическое исследование процессов свободной конвекции бинарной системы «жидкость-газ» осложняется тем, что требует решения системы дифференциальных уравнений движения основной массы жидкости, межмолекулярной диффузии на поверхности раздела фаз, уравнений энергии, выражений профиля температур и скоростей [8, С. 390-391], [9, С. 77-78].

 Значительным недостатком аналитического расчета является то, что он основан на использовании приближенных методов и не учитывает всех факторов тепломассообмена криогенной жидкости в замкнутом пространстве: геометрических особенностей топливного бака, неравномерности распределения притока к поверхностям сосуда, теплофизических свойств жидкой и газообразной фазы СПГ, их зависимости от температуры, начального температурного поля основной массы криопродукта и последующей температурной и компонентной стратификации и др.

С учетом вышесказанного актуальной задачей является максимально приближенное к реальным физическим условиям численное описание процессов гидродинамики, нестационарного тепломассообмена и фазовых переходов на основе применения гидродинамического программного комплекса.

Методы и принципы исследования

Для выполнения подробного исследования распределения параметров криогенного продукта, заполняющего герметичный сосуд, при наличии парового и жидкостного пространства используется математическое моделирование на базе гидродинамического пакета универсальной программы Star-CCM+.

Принцип программного расчета основан на использовании универсальных законов неразрывности, сохранения энергии и импульса, описываемых дифференциальными трехмерными уравнениями Навье-Стокса, осредненных по Рейнольдсу, с помощью которых можно получить распределение параметров сплошной среды в замкнутом объеме, ее теплофизические и гидродинамические особенности [10, С. 156], [11, С. 151].

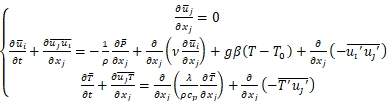   (1)

где t – время; p – плотность;  – компоненты вектора осредненной скорости по осям координат; v – коэффициент кинематической вязкости;  – отклонение фактической температуры от фиксированной средней;  – коэффициент теплового расширения среды;  – осредненные давление и температура;   – турбулентные напряжения (дополнительные напряжения Рейнольдса);  – дополнительный тепловой поток;  – локальные пульсации скорости и температуры.

Получение параметров среды в пространстве сосуда осуществляется при помощи метода конечных (контрольных) объемов – дискретизации уравнений Навье-Стокса, осредненных по времени (уравнений Рейнольдса) – в ходе которого расчетная область разбивается на определенное количество непересекающихся элементарных объемов, совокупность которых называется расчетной сеткой. Для каждого элементарного объема – ячейки – определяются законы сохранения массы импульса и энергии, которые преобразуются в систему алгебраических уравнений относительно скорости, температуры и других характеристик в центрах расчетных ячеек.

Описание турбулентных течений в условиях вычисления процессов сжатия газа, свободно-конвективных движений осуществляется с применением модели турбулентности типа «k-ε», как одной из наиболее эффективных для решения задач подобного рода. Уравнение стандартной модели турбулентности «k-ε» записывается следующими выражениями [12, С. 75]:

    (2)

     (3)

    (4)

где  – турбулентная кинетическая энергия, образованная средними градиентами скорости;  – кинетическая энергия выталкивающей силы; – вклад переменного расширения в общую скорость диссипации, учитывающийся только при больших числах Маха;   – константы, выявленные на основе эмпирических данных.

Для моделирования процесса нагрева в замкнутом объеме необходимо рассматривать бинарную систему с учетом наличия массопереноса конденсацией или испарением на поверхности раздела фаз. В некоторых исследованиях с целью экономии вычислительных ресурсов и сокращения времени программного расчета выполняют две независимые модели парового и жидкостного пространства. Такой подход имеет негативный эффект, связанный с упрощением процесса тепломассопереноса, поскольку не учитывает фактор вертикального перемещения зеркала жидкости. В нашем случае применяется двухфазная модель «жидкость-газ», позволяющая выявить динамику изменения состояния криопродукта на границе раздела.

Поскольку объемная доля метана в сжиженном газе, используемом в качестве топлива для автомобилей, составляет  [13], то исследуемую модель можно представить в качестве однофракционной системы, что позволит снизить ресурс программы на определение нестационарной компонентной стратификации.

Для задачи многофазной среды используется модель Эйлеровой многофазной смеси (Eulerian Multi-Phase Mixture), основанной на использовании метода функции плотности вероятности для получения замкнутой системы уравнений динамики и тепломассопереноса в двухфазном потоке.

Поскольку рассматриваемая среда является гетерогенной (состоит из нескольких фаз), уравнение масс для компонентов смеси будет иметь вид [14, С. 38]:

    (5)

где  – величина, характеризующая долю объема смеси, занимаемой  фазой;  – истинная плотность вещества фазы (масса i-той фазы в единице объема i-той фазы);  – скорость абсолютного движения фазы;  – величина, характеризующее интенсивность перехода массы из j-той в i-тую составляющую в единице объема смеси и в единицу времени (массовый приток).

Уравнение движения для фаз в отдельности (закон сохранения импульса) записывается следующим образом [14, С. 42]:

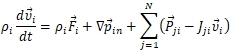    (6)

где – массовые (объемные) силы, отнесенные к единице массы жидкости и называемые напряженностью поля сил;  – поверхностная сила, отнесенная к единице площади поверхности (напряжение);  – интенсивность обмена импульсом между j-той и i-той составляющими.

 Описание взаимодействий между двумя агрегатными состояниями топлива осуществляется с помощью подмоделей Volume Of Fluid: взаимодействие фаз (Phase Interaction), Кипение (Boiling) и Rohsenow Кипение (Rohsenow Boiling) [15, С. 6, 11]. Стоит отметить, что модель Volume Of Fluid, задающая процессы испарения и конденсации, предполагает наличие границы раздела жидкой и газообразной фаз [16, С. 3].

Основные результаты

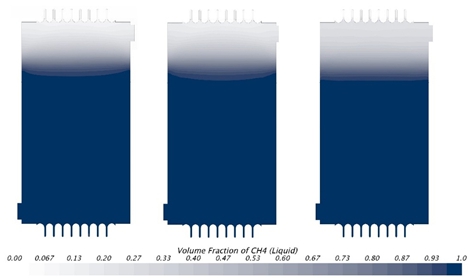
Как можно увидеть (см. рисунок 2) со временем хранения криогенного топлива происходит изменение расположения границы раздела фаз вдоль вертикальной оси сосуда с повышением доли парового пространства, что связано с преобладанием скорости теплопередачи от пара над скоростью отводом тепла к жидкости [8, С. 389]. Следовательно, для данной конструкции сосуда (при условиях стационарного режима хранения) начального объема парового пространства, соответствующего  геометрического объема бака , будет достаточно для перехода части жидкой фазы СПГ в газообразное состояние и перемещения зеркала жидкости вертикально вниз.

Рис. 2 – Поля объемной доли жидкой фазы (CH₄ luquid) при осуществлении сходимости задачи

 

 Необходимо добавить, что при рассмотрении профиля распределения фаз «жидкость-пар» отчетливо прослеживается непрекращающееся явление конвективного тепломассопереноса под воздействием архимедовых сил и вязких напряжений, проявляющееся в формировании зоны насыщенного пара, доля жидкой фазы в которой варьируется от 60% до 84%.

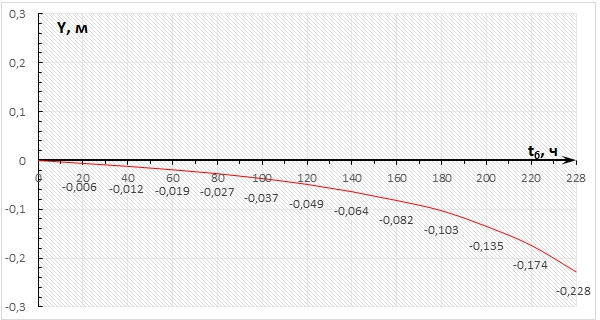
В ходе анализа полученных данных положения зеркала жидкого метана при реализации бездренажного хранения прослеживается опускание границы раздела фаз по вертикальной оси. На оси ординат в качестве нуля принято исходное положение плоскости жидкого метана после заполнения сосуда. При достижения критического давления в емкости  [17] уровень топлива снизился на 0,228 м (см. рисунок 3). Стоит отметить, интенсивность кипения жидкой фазы возрастает по мере хранения криотоплива.

Рис. 3 – Изменение положения уровня раздела фаз по времени бездренажного хранения

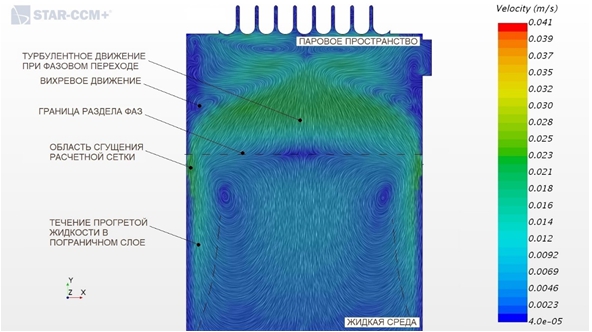
На примере полученного поля распределения скоростей с наложением линий тока в верхней части криогенного сосуда (см. рисунок 4) подтверждены результаты практических работ по изучению естественной конвекции в условиях нагрева боковых стенок. Во-первых, установлено наличие восходящих течений прогретой жидкости в пограничном слое  с образованием вихрей на расстоянии 0,04 м от плоских поверхностей бака при повороте течений к средней точке объема. Во-вторых, наблюдается увеличение толщины пограничного слоя δ с расстоянием вдоль стенки от  . В-третьих, в слое температурного расслоения формируется переходное движение  от плоскости фазового раздела в нижнюю зону. Сжиженный газ здесь находится в состоянии перемешивания с температурой выше температуры ядра криопродукта.

Рис. 4 – Гидродинамическое поле с отображением линейных интегралов скоростей в верхней части емкости

 

Как известно для аналитического рассмотрения модели температурного расслоения используется ряд упрощений и выведенных соотношений, позволяющих описать движение жидкости у обогреваемой поверхности, выявить толщину и время слоя температурного расслоения, определить температуру поверхности жидкости [8, С. 420, 436-439].

Уравнение, характеризующее движение криопродукта внутри горизонтального цилиндра:

     (7)

где a – коэффициент теплоотдачи стенки сосуда,  – внешний диаметр цилиндра,  – коэффициент теплопроводности при температуре  – температура стенки,  – среднемассовая температура,  – коэффициент объемного расширения при  – коэффициент динамической вязкости при .

Уравнение соотношения перепада температуры, времени хранения и толщины слоя температурного расслоения:

    (8)

где – температура поверхности раздела,   – температура неперемешанной жидкости,   – плотность теплового потока в боковой стенке,  – высота жидкости, R – радиус сосуда, м; Pr – число Прандтля;  – толщина слоя температурного расслоения, м;  t – время хранения, с.

Полученные данные математического моделирования показали, что применяемые допущения теоретического анализа вносят значительные корректировки по отношению к результатам, выявленным при выполнении численного исследования процесса изохорного нагрева бинарной системы «жидкость-пар». Такие упрощения как постоянство среднемассовой температуры , описание температурного расслоения профилем ψ, не зависящем от времени и радиального расстояния, могут быть применимы в ходе аналитического исследования на небольших временных отрезках (малых изменениях давления ), поскольку процесс изменения температур СПГ в реальном криобаке имеет длительный характер и при программном расчете требует большого числа итераций. Однако допущение отсутствия тепло- и массообмена на границе раздела фаз вносит значительную погрешность при осуществлении расчетов, описании процессов на границе раздела фаз и выявлении динамики роста избыточного давления в баке.

Заключение  

Результаты численного моделирования термодинамических процессов криопродукта в гофрированном сосуде перспективной модели топливного бака на базе программного комплекса Star-CCM+ показали, что развитие пограничного слоя начинается не в нижней точке криососуда и зависит от геометрии бака, температурного градиента, плотности теплового потока, его равномерности и др.

Зона однородной температуры (неперемешанная жидкость) при условии рассмотрения однокомпонентного топлива (объемная доля  в СПГ составляет единицу) и отсутствия фракционной стратификации при наличии «старой» и «новой» жидкой фазы остается стабильной на длительном промежутке времени без потери гидродинамической устойчивости.

Время наступления критического избыточного давления  в баке на практике оказывается меше, чем при исследовании аналитической модели, вследствие существования неучитываемых при инженерном расчете теплофизических и  гидродинамических факторов, таких как формирование слоя температурного расслоения, граничащего с газообразной средой слоем прогретой жидкости, что исключает процесс конденсации пара и, как следствие, усиливает скорость повышения рабочего давления.

 Наличие гофрированных участков сосуда не оказывает значительного воздействия на формирование температурных и гидродинамических полей в общем объеме исследуемого внутреннего пространство.

Конфликт интересов Не указан.	Conflict of Interest None declared.

Список литературы / References

1. Мовчан Е. П. Создание эффективных автомобильных криобаков для СПГ / Е. П. Мовчан // Технические газы. – 2009. – №3. – С. 68–72.
2. Бармин И. В. Сжиженный природный газ вчера, сегодня, завтра / И. В. Бармин, И. Д. Кунис. – М.: Изда-во МГТУ им. Н.Э. Баумана, 2009. – 256 с.
3. Каганер М. Г. Тепловая изоляция с использованием вакуума / М. Г. Каганер. – М.: ВНИИКИМАШ, 1963. – 45 с.
4. Пат. 118717 Российская Федерация, МПК F17C 9/00. Бак криогенный топливный транспортного средства, работающего на сжиженном природном газе / Колгушкин Ю. В.; заявитель и патентообладатель ОАО «НПО «ГЕЛИЙМАШ». – № 2012110491/06; заявл. 20.03.2012; опубл. 27.07.2012, Бюл. № 21. – 11 с.
5. Архаров А. М. Криогенные системы: Учебник для студентов вузов по специальностям «Техника и физика низких температур» и «Холодильная, криогенная техника и кондиционирование»: В 2 т. Т.2. Основы проектирования аппаратов, установок и систем / А. М. Архаров, И. А. Архаров, В. П. Беляков и др.; под ред. А. М. Архарова, А. И. Смородина. – М.: Машиностроение, 1999. – 720 с.
6. Сорокин А. П. Сжиженный метан за рубежом / А. П. Сорокин, Л.М. Черняк. – М.: «НЕДРА», 1965. – 135 с.
7. Технические данные. Газовый баллон. [Электронный ресурс]. – URL: stpi.it.volvo.com/STPIFiles/Volvo/FactSheet/ LGAS115,%20LGAS155,%20LGAS205_Rus_01_309253877.pdf (дата обращения: 06.04.2020).
8. Кларк Д. Криогенная теплопередача. – В кн.: Успехи теплопередачи: Пер. с англ. / Д. Кларк. – М.: Мир, 1971. – С. 361–567.
9. Беляков В.П. Криогенная техника и технология / В.П. Беляков. – М.: Энергоиздат, 1982. – 272 с.
10. Уляшева В. М. Численное моделирование распределения воздуха веерными диффузорами в офисных помещениях / В. М. Уляшева, А. А. Вдовичев // Материалы XVI Международной научной конференции «Качество внутреннего воздуха и окружающей среды». – 2018. – №1. – С. 154–159.
11. Солдатов Е. С. Численное исследование нестационарного тепломассообмена в криогенном резервуаре долговременного хранения с подвижной границей раздела фаз / Е.С. Солдатов // Вестник Тюменского государственного университета. Физико-математическое моделирование. Нефть, газ, энергетика. – 2019. – Т. 5. – №2. – С. 148–159.
12. Кузьминов А. В. Метод расчета турбулентных течений несжимаемой жидкости на основе двухслойной (k-ε)-модели / А. В. Кузьминов, В. Н. Лапин, С. Г. Черный // Вычислительные технологии. – 2001. – Т. 6. – № 5. – С. 73-86.
13. ГОСТ Р 57431-2017. Газ природный сжиженный. Общие характеристики. – Введ. 2018–01–01. – М.: Стандартинформ, 2017. – 16 с.
14. Саровский инженерный центр. Руководство пользователя STAR-CCM+ версии 8.02. Перевод документации CD-adapco. Моделирование кипения с использованием модели Объема Жидкости (VOF) (VOF: Boiling). 2010. – 25 с.
15. Великанова Ю. В. Гидромеханика многофазных сред: учебное пособие / Ю. В. Великанова. – Самара.: Самарский государственный технический университет, 2009. – С. 166.
16. Алешин А. Е. Компьютерное моделирование тепломассопереноса в канале регенеративного теплообменника / А. Е. Алешин, А. В. Циганкова, Т. В. Рябова // Научный журнал НИУ ИТМО. Серия «Холодильная техника и кондиционирование». – 2015. – № 1. – С. 1-7.
17. ГОСТ Р 56217-2014. Автомобильные транспортные средства, использующие газ в качестве моторного топлива. Общие технические требования к эксплуатации на сжиженном природном газе, техника безопасности и методы испытаний. – Введ. 2015–06–01. – М.: Стандартинформ, 2015. – 20 с.

Список литературы на английском языке / References in English

1. Movchan E. P. Sozdaniye effektivnykh avtomobilnykh kriobakov dlya SPG [Creating efficient automotive cryobanks for LNG] / E. P. Movchan // Tekhnicheskiye gazy. – 2009. – №3. – P. 68–72. [in Russian]
2. Barmin I. V. Szhizhennyy prirodnyy gaz vchera. segodnya. Zavtra [Liquefied natural gas yesterday, today, tomorrow] / I. V. Barmin. I. D. Kunis. – M.: Izda-vo MGTU im. N.E. Baumana. 2009. – 256 p. [in Russian]
3. Kaganer M. G. Teplovaya izolyatsiya s ispolzovaniyem vakuuma [Thermal insulation using vacuum] / M. G. Kaganer. – M.: VNIIKIMASh. 1963. – 45 p. [in Russian]
4. Pat. 118717 Russian Federation. MPK F17C 9/00. Bak kriogennyy toplivnyy transportnogo sredstva. rabotayushchego na szhizhennom prirodnom gaze [Tank cryogenic fuel vehicle operating on liquefied natural gas] / Kolgushkin Yu. V.; applicant and patent holder of open joint-stock company "research and production association «GELIYMASH». – № 2012110491/06; appl. 20.03.2012; publ. 27.07.2012. Byul. № 21. – 11 p. [in Russian]
5. Arkharov A. M. Kriogennyye sistemy: Uchebnik dlya studentov vuzov po spetsialnostyam «Tekhnika i fizika nizkikh temperatur» i «Kholodilnaya. kriogennaya tekhnika i konditsionirovaniye»: V 2 t. T.2. Osnovy proyektirovaniya apparatov. ustanovok i system [Cryogenic systems: A textbook for university students on the specialties «Technics and Physics of Low Temperatures» and «Refrigeration, Cryogenic Technique and Conditioning»: In 2 vols. T.2. Fundamentals of designing apparatuses, installations and systems] / A. M. Arkharov. I. A. Arkharov. V. P. Belyakov i dr.; pod red. A. M. Arkharova. A. I. Smorodina. – M.: Mashinostroyeniye. 1999. – 720 p. [in Russian]
6. Sorokin A. P. Szhizhennyy metan za rubezhom [Liquefied methane abroad] / A. P. Sorokin. L.M. Chernyak. – M.: «NEDRA». 1965. – 135 p. [in Russian]
7. Tekhnicheskiye dannyye. Gazovyy ballon [Technical details. Gas bottle] [Electronic resource]. – URL: stpi.it.volvo.com/STPIFiles/Volvo/FactSheet/ LGAS115.%20LGAS155.%20LGAS205_Rus_01_309253877.pdf (accessed: 07.04.2020) [in Russian]
8. Klark D. Kriogennaya teploperedacha. – V kn.: Uspekhi teploperedachi: Per. s angl. [Cryogenic heat transfer. - In the book: Successes in heat transfer] / D. Klark. – M.: Mir. 1971. – P. 361–567. [in Russian]
9. Belyakov V.P. Kriogennaya tekhnika i tekhnologiya [Cryogenic Engineering and Technology] / V.P. Belyakov. – M.: Energoizdat. 1982. – 272 p. [in Russian]
10. Ulyasheva V. M. Chislennoye modelirovaniye raspredeleniya vozdukha veyernymi diffuzorami v ofisnykh pomeshcheniyakh [Numerical simulation of air distribution by fan diffusers in office premises] / V. M. Ulyasheva. A. A. Vdovichev // Materialy XVI Mezhdunarodnoy nauchnoy konferentsii «Kachestvo vnutrennego vozdukha i okruzhayushchey sredy». – 2018. – №1. – P. 154–159. [in Russian]
11. Soldatov E. S. Chislennoye issledovaniye nestatsionarnogo teplomassoobmena v kriogennom rezervuare dolgovremennogo khraneniya s podvizhnoy granitsey razdela faz [Numerical study of unsteady heat and mass transfer in a cryogenic long-term storage tank with a moving phase boundary] / E.S. Soldatov // Vestnik Tyumenskogo gosudarstvennogo universiteta. Fiziko-matematicheskoye modelirovaniye. Neft. gaz. energetika. – 2019. – T. 5. – №2. – P. 148–159. [in Russian]
12. Kuzminov A. V. Metod rascheta turbulentnykh techeniy neszhimayemoy zhidkosti na osnove dvukhsloynoy (k-ε)-modeli [A method for calculating turbulent flows of an incompressible fluid based on a two-layer (k-ε) model] / A. V. Kuzminov. V. N. Lapin. S. G. Chernyy // Vychislitelnyye tekhnologii. – 2001. – T. 6. – № 5. – P. 73-86. [in Russian]
13. GOST R 57431-2017. Gaz prirodnyy szhizhennyy. Obshchiye kharakteristiki [Natural liquefied gas. General characteristics]. – Vved. 2018–01–01. – M.: Standartinform. 2017. – 16 p. [in Russian]
14. Sarovskiy iyenzhenernyy tsentr. Rukovodstvo polzovatelya STAR-CCM+ versii 8.02. Perevod dokumentatsii CD-adapco. Modelirovaniye kipeniya s ispolzovaniyem modeli Obyema Zhidkosti (VOF) (VOF: Boiling) [Sarov Engineering Center. STAR-CCM + Version 8.02 User Guide. Translation of CD-adapco documentation. Simulation of boiling using the model of the Volume of fluid (VOF) (VOF: Boiling)]. 2010. – 25 p. [in Russian]
15. Velikanova Yu. V. Gidromekhanika mnogofaznykh sred: uchebnoye posobiye [Hydromechanics of multiphase media: a training manual] / Yu. V. Velikanova. – Samara.: Samarskiy gosudarstvennyy tekhnicheskiy universitet. 2009. – P. 166. [in Russian]
16. Aleshin A. E. Kompyuternoye modelirovaniye teplomassoperenosa v kanale regenerativnogo teploobmennika [Computer simulation of heat and mass transfer in the channel of a regenerative heat exchanger] / A. E. Aleshin. A. V. Tsigankova. T. V. Ryabova // Nauchnyy zhurnal NIU ITMO. Seriya «Kholodilnaya tekhnika i konditsionirovaniye». – 2015. – № 1. – P. 1-7. [in Russian]
17. GOST R 56217-2014. Avtomobilnyye transportnyye sredstva. ispolzuyushchiye gaz v kachestve motornogo topliva. Obshchiye tekhnicheskiye trebovaniya k ekspluatatsii na szhizhennom prirodnom gaze. tekhnika bezopasnosti i metody ispytaniy [Automobile vehicles using gas as a motor fuel. General technical requirements for operation on liquefied natural gas, safety measures and test methods]. – Vved. 2015–06–01. – M.: Standartinform. 2015. – 20 p. [in Russian]