О ПРЕДСТАВЛЕНИИ СТАБИЛЬНОГО ЭЛЕМЕНТА СВОБОДНОЙ НИЛЬПОТЕНТНОЙ ГРУППЫ
Ковыршина А.И.1, Лапшина Е.С.2
1Кандидат физико-математических наук,
2Кандидат физико-математических наук,
Иркутский государственный университет
О ПРЕДСТАВЛЕНИИ СТАБИЛЬНОГО ЭЛЕМЕНТА СВОБОДНОЙ НИЛЬПОТЕНТНОЙ ГРУППЫ
Аннотация
Для того чтобы найти нетривиальный стабильный элемент свободной нильпотентной группы необходимо выделить все возможные виды базисных коммутаторов, из которых в дальнейшем строится кандидат на стабильный элемент. Статья посвящена описанию трех видов коммутаторов, каждый из которых тесно связан с двумя другими. Так, если в представление стабильного элемента входят коммутаторы одного из видов, то и остальные виды должны быть представлены в разложении этого элемента. Рассматривается свободная нильпотентная группа ранга 3 ступени 12.
Ключевые слова: автоморфизмы групп, неподвижные точки, нильпотентные группы.
Kovyrshyna A.I.1, Lapshyna E.S.2
1PhD in Physics and Mathematics,
2PhD in Physics and Mathematics,
Irkutsk State University
ON REPRESENTATION OF A STABLE ELEMENT OF A FREE NILPOTENT GROUP
Abstract
In order to find a nontrivial stable element of a free nilpotent group, it is necessary to isolate all possible types of basic commutators that are later used to build a candidate for a stable element. The article is devoted to the description of three kinds of switches; each of them is closely related to the other two. For example, if the representation of a stable element includes commutators of one of the types, then the remaining species must be represented in the expansion of this element. We consider a free nilpotent group of rank 3 and of order 12.
Keywords: automorphisms of groups, fixed points, nilpotent groups.
Стабильными элементами называются элементы группы, которые неподвижны относительно всех ее автоморфизмов.
Интерес к проблеме существования нетривиальных стабильных элементов в свободных нильпотентных группах обусловлен результатами работ Ф. Вефера (1949 г.) и М. Барроу (1958 г.) в области изучения инвариантов Ли свободных колец Ли. Условия на ранг и ступень свободных нильпотентных групп, в которых существуют стабильные элементы, получили А. Папистас [2], Е. Форманек [3]. Методы построения стабильных элементов с представлением некоторых серий таких элементов представлены В.В. Блудовым [1], А.И. Ковыршиной [4, 5]. В работе [4] показан пример нетривиального стабильного элемента, который представлен в виде произведения 22 базисных коммутаторов одного вида. Настоящая статья посвящена нетривиальному стабильному элементу, в разложении которого участвуют 36 коммутаторов трех различных видов. При этом, исключение хотя бы одного коммутатора любого из трех видов делает элемент нестабильным.
Рассмотрим следующие подмножества базисных коммутаторов третьего коммутанта группы ![]() – совокупность коммутаторов вида
– совокупность коммутаторов вида ![]() – совокупность коммутаторов вида
– совокупность коммутаторов вида ![]() – совокупность коммутаторов вида
– совокупность коммутаторов вида ![]() . Введем обозначения для следующих автоморфизмов группы
. Введем обозначения для следующих автоморфизмов группы ![]() со свободными образующими
со свободными образующими ![]() :
:
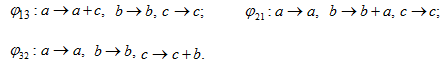
Известно, что если элемент ![]() группы
группы ![]() удовлетворяет условию
удовлетворяет условию ![]() , то
, то ![]() – стабильный элемент.
– стабильный элемент.
В настоящей работе доказана следующая теорема:
Теорема: Пусть ![]() – линейная комбинация базисных коммутаторов, хотя бы один из которых принадлежит множеству
– линейная комбинация базисных коммутаторов, хотя бы один из которых принадлежит множеству ![]() . Если
. Если ![]() – нетривиальный стабильный элемент группы
– нетривиальный стабильный элемент группы ![]() , то число коммутаторов, участвующих в представлении элемента
, то число коммутаторов, участвующих в представлении элемента ![]() не меньше 36.
не меньше 36.
Доказательство. Для описания процесса построения нетривиального стабильного элемента введем обозначения базисных коммутаторов указанных множеств. Базисными элементами множества ![]() с однородным вхождением образующих являются:
с однородным вхождением образующих являются:
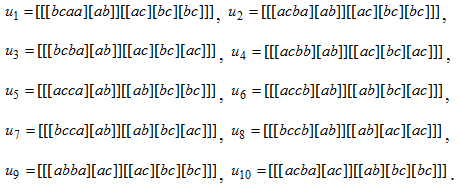
Мы не можем ограничиться рассмотрением линейной комбинации только элементов множества ![]() , так как после действия на них автоморфизмами, происходит нарушение базисности и меняется вид базисных коммутаторов. Так, в образ
, так как после действия на них автоморфизмами, происходит нарушение базисности и меняется вид базисных коммутаторов. Так, в образ ![]() входит коммутатор
входит коммутатор ![]() , который является элементом множества
, который является элементом множества ![]() . При конструировании кандидата на стабильный элемент, необходимо добавить базисные коммутаторы множества
. При конструировании кандидата на стабильный элемент, необходимо добавить базисные коммутаторы множества ![]() , которые обозначим так:
, которые обозначим так:
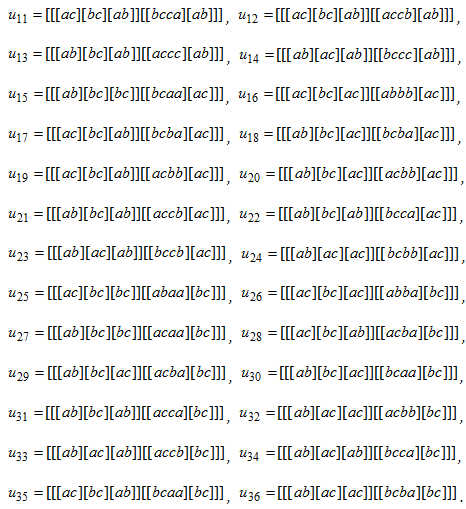
Рассмотрим в элементы каких множеств переходят коммутаторы из ![]() после применения к ним автоморфизмов вида
после применения к ним автоморфизмов вида ![]() . Некоторые элементы из
. Некоторые элементы из ![]() содержат подкоммутатор
содержат подкоммутатор ![]() , образ которого под действием автоморфизма
, образ которого под действием автоморфизма ![]() равен
равен ![]() . Коммутатор
. Коммутатор ![]() не является базисным, его разложение на базисные имеет вид
не является базисным, его разложение на базисные имеет вид ![]() . Поэтому, в результате применения
. Поэтому, в результате применения ![]() , например, к элементу
, например, к элементу ![]() мы получим следующую сумму базисных коммутаторов:
мы получим следующую сумму базисных коммутаторов:
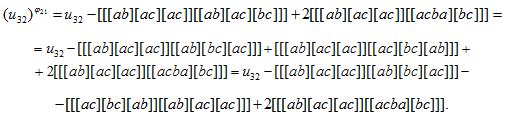
В нее входят коммутаторы, принадлежащие ![]() . Таким образом, в автоморфном образе элементов из кроме элементов из содержатся элементы из . Введем обозначения базисных коммутаторов из
. Таким образом, в автоморфном образе элементов из кроме элементов из содержатся элементы из . Введем обозначения базисных коммутаторов из ![]() :
:
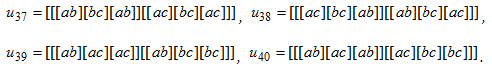
Составим линейную комбинацию 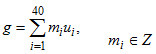 всех базисных коммутаторов множеств
всех базисных коммутаторов множеств ![]() . Последовательно будем действовать на
. Последовательно будем действовать на ![]() автоморфизмами указанных выше видов. После перевода всех небазисных коммутаторов в сумму базисных, устраиваем разбиение элементов в зависимости от их принадлежности множествам
автоморфизмами указанных выше видов. После перевода всех небазисных коммутаторов в сумму базисных, устраиваем разбиение элементов в зависимости от их принадлежности множествам ![]() с целью получения условий на коэффициенты
с целью получения условий на коэффициенты ![]() .
.
После применения автоморфизма ![]() к элементу
к элементу ![]() и приведения всех коммутаторов к базисному виду, выделим линейную комбинацию элементов из
и приведения всех коммутаторов к базисному виду, выделим линейную комбинацию элементов из ![]() :
:
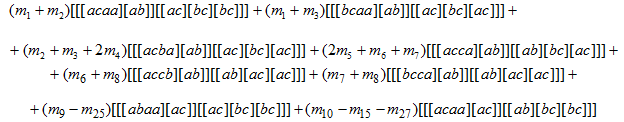
Для вычисления значений ![]() необходимо приравнять к нулю коэффициенты этого выражения. Как было отмечено ранее, в автоморфный образ элемента
необходимо приравнять к нулю коэффициенты этого выражения. Как было отмечено ранее, в автоморфный образ элемента ![]() входят коммутаторы из
входят коммутаторы из ![]() (не по причине включения в
(не по причине включения в ![]() базисных коммутаторов из названного множества). Поэтому нельзя ограничиться рассмотрением лишь указанной суммы, необходимо также получить линейную комбинацию элементов из
базисных коммутаторов из названного множества). Поэтому нельзя ограничиться рассмотрением лишь указанной суммы, необходимо также получить линейную комбинацию элементов из ![]() :
:
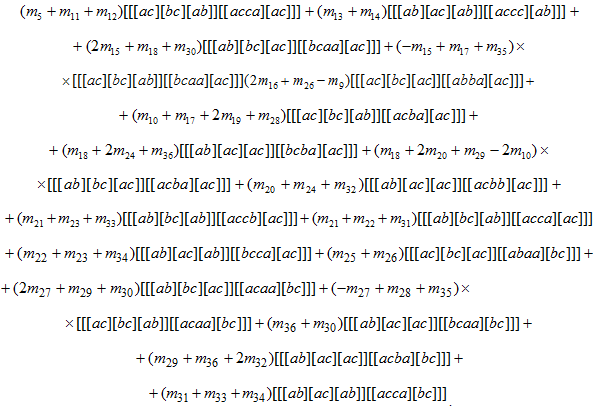
Аналогичным образом действуем автоморфизмами ![]() . Чтобы не перегружать данную работу коммутаторными вычислениями, запишем итоговую систему линейных уравнений, решение которой дает целые значения для коэффициентов, участвующих в выражении элемента
. Чтобы не перегружать данную работу коммутаторными вычислениями, запишем итоговую систему линейных уравнений, решение которой дает целые значения для коэффициентов, участвующих в выражении элемента ![]() через базисные:
через базисные:
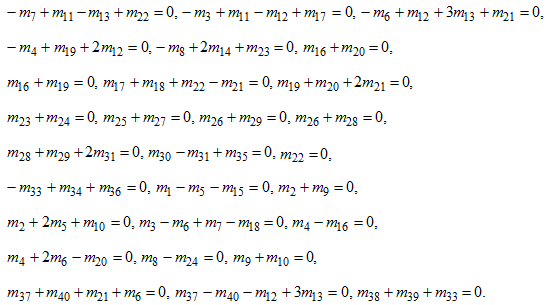
Общее решение объединенной системы уравнений имеет вид:
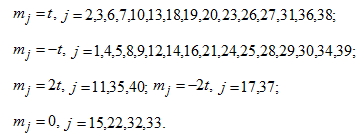
Так как все коэффициенты зависят от одной свободной переменной ![]() , то число коммутаторов, участвующих в представлении элемента стабильного элемента не меньше 36. Теорема доказана.
, то число коммутаторов, участвующих в представлении элемента стабильного элемента не меньше 36. Теорема доказана.
Список литературы / References
- Блудов В.В. Неподвижные точки относительно всех автоморфизмов в свободных нильпотентных группах/ В.В. Блудов //Третий Сибирский конгресс по прикладной и индустриальной математике: тезисы докл. – Ч.5. – Новосибирск, 1998.
- Papistas A. A note on fixed points of certain relatively free nilpotent groups / A. Papistas //Communications in algebra. – 2001. – No. 29. –P. 4693-4699.
- Formanek E. Fixed points and centers of automorphism groups of free nilpotent groups / E. Formanek // Communications in algebra. – 2002. – No. 30. – Pp. 1033-1038.
- Ковыршина А.И. Неподвижные элементы в свободных нильпотетных группах ранга три / А.И. Ковыршина // Вестник НГУ. Серия: Математика, механика, информатика. – 2008. – Т.8, вып.2. – С. 85–91.
- Ковыршина А.И. Стабильные элементы в свободных нильпотентных группах ранга три/ А.И. Ковыршина // Вестник Омского университета. – 2010. – №4 (58). – С. 20–23.
Список литературы на английском языке / References in English
- Bludov V.V. Nepodvizhnye tochki otnositel'no vseh avtomorfizmov v svobodnyh nil'potentnyh gruppah [Fixed points with respect to all automorphisms in free nilpotent groups] / V.V. Bludov // Tretij Sibirskij kongress po prikladnoj i industrial'noj matematike: tezisy dokladov [Third Siberian Congress on Industrial and Applied Mathematics]. Novosibirsk, 1998. Part 5. [in Russian]
- Papistas A. A note on fixed points of certain relatively free nilpotent groups/ A. Papistas //Communications in algebra. – 2001. – No. 29. –P. 4693–4699.
- Formanek E. Fixed points and centers of automorphism groups of free nilpotent groups / E. Formanek // Communications in algebra. – 2002. – No. 30. – P. 1033–1038.
- Kovyrshina A.I. Nepodvizhnye jelementy v svobodnyh nil'potetnyh gruppah ranga tri [Fixed points in the free nilpotent groups of rank three] / A.I. Kovyrshina // Vestnik NGU. Ser. Matematika, mehanika, informatika. [Vestnik Novosibirsk State University. Mathematics]. – 2008. – V.8. No. 2 – P. 85–91. [in Russian]
- Kovyrshina A.I. Stabil'nye jelementy v svobodnyh nil'potentnyh gruppah ranga tri [Fixed points with respect to all automorphisms of the free nilpotent groups for three generators] / A.I. Kovyrshina // Vestnik Omskogo universiteta. [Herald of Omsk University]. – 2010. – No. 4 (58). – P. 20–23. [in Russian]
