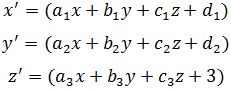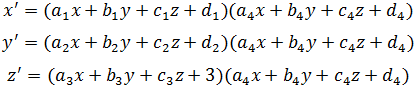МЕТОДЫ КЛАССИЧЕСКОЙ ПРИКЛАДНОЙ ГЕОМЕТРИИ В ТЕХНИЧЕСКОМ ПРИМЕНЕНИИ

Якунин В. И.¹, Гузненков В. Н.², Журбенко П. А.³, Осипук А. А.⁴

¹Доктор технических наук; ²Доктор педагогических наук, доцент; ³Старший преподаватель; ⁴Ассистент, Московской государственный технический университет имени Н. Э. Баумана

МЕТОДЫ КЛАССИЧЕСКОЙ ПРИКЛАДНОЙ ГЕОМЕТРИИ В ТЕХНИЧЕСКОМ ПРИМЕНЕНИИ

Аннотация

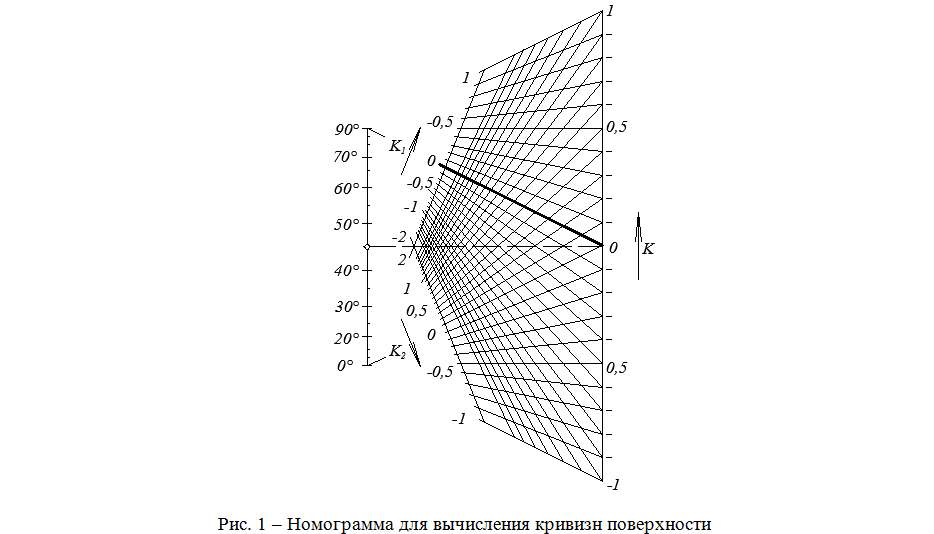
В статье рассмотрены модели в классической геометрии, их развитие, способы создания, возможности сочетания аналитических и графических методов, влияние начертательной геометрии на конструирования поверхностей. Приведено исследование поверхностей общего вида, как возможность внедрения в классическое содержание смежных геометрических дисциплин. Рассмотрено построение бинарного поля номограммы, позволяющего анализировать кривизны в любых точках криволинейной поверхности, заданной аналитически или неявной форме. Получены результаты для всех минимальных поверхностей.

Ключевые слова: исследование поверхностей, номографический метод, начертательная геометрия.

Yakunin V. I.¹, Guznenkov V. N.², Zhurbenko P. A.³, Osipuk A. A.⁴

¹PhD in Engineering, ²PhD in Pedagogy, Associate professor; ³Senior lecturer, ⁴Teacher assistant, Bauman Moscow State Technical University

APPLIED MOTHODS OF CLASSICAL GEOMETRY IN TECHNICAL APPLICATIONS

Annotation

The article considers the models of classical geometry, their development, methods of creation, opportunities combination of analytical and graphical methods, descriptive geometry influence on the design surface.  Surface general type research was conducted as the possibility of introducing the classical geometric content related disciplines. In this topic consider the construction of a binary field nomogram that allows to analyze the curvature at any point of the curved surface defined analytically or implicitly. The results obtained for all minimal surfaces.

Keywords: research of surfaces, nomogrammic method, descriptive geometry.

Основания начертательной геометрии относятся к XVIII-XIX вв. Это была очень дифференцируемая научная дисциплина, элементы которой, и вместе с тем её основное научное содержание, были разработаны и систематизированы выдающимся французским геометром, разносторонним мыслителем и философом Гаспаром Монжем. Этот учёный придавал большое значение начертательной геометрии как глубокой научной и педагогической дисциплине.

Достаточно привести его педагогический комментарий: «Если бы мне снова пришлось начать эту работу (речь идёт о написании курса начертательной геометрии),  я напечатал бы её в два столбца: в первом я поместил бы решения геометрических задач путём вычисления, а во втором – решение тех же задач, но исполненное путём графических построений. Читатели были бы, пожалуй, очень удивлены, увидев, что второй столбец почти всегда заслуживал бы предпочтение, как по ясности, так и по простоте доказательств». [1]

Всё это дало возможность установить двойственный характер начертательной геометрии, причислив её к классу прикладный наук, и присвоить ей второе, более общее определение – прикладной геометрии. Это, в частности, объясняется тем, что начертательная геометрия играет значительную роль в самой математике, являясь её составляющей в механике, физике, а также в кристаллографии, живописи, медицине, в конструировании самых разнообразных объектов в самолётостроении, вертолётостроении и т.д. Об этом всерьёз и основательно упоминается  в книге Джона Хоргана «Конец науки (или взгляд на ограниченность знания на закате века науки)», С.-П. «Амфора», 2001 г.: «Прикладная наука будет жить долгое время, т.к. учёные продолжат разработку новых универсальных конструкций и материалов: более быстрых и сложных компьютеров, новых и эффективных генно-инженерных технологий, делающих нас здоровее, сильнее, увеличивающих продолжительность жизни и всё более полно опирающихся на достижения математики, в том числе и высшей прикладной геометрии».

Следует отметить важнейшую особенность всякого геометрического знания – степень её визуализации, что способствует универсальной возможности её применения.

Так, ещё академик А.Н. Колмогоров писал: «Однако везде, где это возможно, математики стремятся сделать изучаемые ими проблемы геометрически наглядными, поэтому геометрическая интуиция, геометрическое воображение, пространственные представления, всевозможные геометрические их интерпретации играют существенную роль в процессе изучения различных разделов математики, физики, техники и т.д.».

Если принять во внимание типологию и систематику процесса возникновения новых областей знания, то прикладную геометрию можно отнести как к типу А, так и к типу С. Поясним всё сказанное, ссылаясь на соответствующие характеристики.

Тип А. Процесс его возникновения складывается из возможностей и потребностей исследования новых, неизвестных прежде, или исследовавшихся спорадически предметных областей. В нашем случае основной составляющей является пространство решения общих технических проблем, основанное на геометрических методах, применяющихся в начертательной геометрии плюс САПР (здесь подразумевается смысловой эквивалент английского слова CAD, означающего проектирование с помощью ЭВМ). В содержательном смысле более подробно это геометрическое конструирование,  возможности автоматизации которого обеспечиваются использованием цифровых вычислительных средств, а также как создание и преобразование накопленной информации с использованием ЭВМ. В современном истолковании это понимается как машинное геометрическое моделирование.

Тип С. Непосредственные связи двух или трёх традиционных дисциплин способствует консолидации предметов отдельных наук и ведут к возникновению пограничных дисциплин. В этом случае ведущую роль приобретают те проблемы, которые разрешаются на стыке отдельных областей знания. Таким образом, возникновение новых областей знания происходит не в результате произвола и субъективных склонностей учёных, а представляет сугубо объективный процесс.

Образование такого рода пограничных научных дисциплин ничего не меняет в дальнейшем существовании «материнских дисциплин». В прошлом веке для инженерной подготовки основной задачей начертательной геометрии было – научить мыслить пространственно, решать задачи на эпюре Монжа, в аксонометрии и т.д.

От других геометрических наук, т.е. от аналитической, дифференциальной или проективной геометрий, начертательная геометрия отличается своим методом. В самом деле, метод начертательной геометрии состоит в построении и изучении отображений объектов действительного мира, позволяющих устанавливать необходимые закономерности и решать относящиеся к этой области задачи. Очень важно подчеркнуть, что начертательная геометрия как наука обогащалась и обогащается новыми идеями и новыми методами исследования, что вполне естественно, если учитывать неравномерность развития других наук. Так, на начертательную геометрию серьёзное и благотворное влияние оказало развитие аналитической и проективной геометрии, многомерной геометрии и топологии.

Но если говорить о состоянии высшей начертательной геометрии в XX и XXI столетиях, то сейчас, как и раньше, имели и имеют большое значение прикладные задачи в области механики, теории механизмов и машин, новой техники, а также САПР и фундаментальных результатов вычислительной техники.

Так в XX столетии известный советский геометр из Ярославля профессор З.А. Скопец доказал пригодность и применимость методов начертательной геометрии к исследованию и решению задач проективной неевклидовой геометрии. По этому поводу сохраняет свою актуальность высказывание выдающегося французского геометра, основателя аналитической геометрии, Р. Декарта: «Все науки настолько связаны между собой, что легче изучать их все сразу, нежели какую-либо одну из них в отдельности от всех прочих». Говоря о геометрии в широком смысле слова, уместно вспомнить о тех фундаментальных идеях, которые высказал немецкий геометр Ф. Клейн в своей «Эрлангенской программе» (1872).

Речи идёт о строении геометрии, об её основаниях, базирующихся на теории преобразований. Клейн предложил систематику геометрических дисциплин по классу преобразований, превалирующих в них. За основу взяты линейные аффинные преобразования, т.е. целые линейные подстановки переменных x,y,z, т.е.

Таким образом речь идёт о тех элементах, которые остаются неизменным относительно определённо1 группы преобразований. Также элементы называются инвариантами. По Клейну геометрия является такими образом теорией инвариантов линейных подстановок.

Итак, аффинная геометрия это, по существу теория инвариантов аффинных преобразований. Используя теорию инвариантов, можно построить проективную геометрию на основании проективных, т.е. дробно-линейных преобразовании, а именно:

которые включают аффинные преобразования как частные случаи. Итак, проективная геометрия выступает как теория инвариантов проективных преобразований.

Следуя тому же принципу можно перейти от метрической геометрии также и к другим видам геометрий. Итак, здесь уместно объяснить, что различные геометрии различаются группой преобразований, относительно которых они инвариантны, методом и аксиоматической базой. Так, на начальном этапе изложения в аналитической геометрии рассматриваются свойства тех же линейных образов пространства, что и в начертательной геометрии, но для их исследования используется аппарат алгебры, в дифференциальной геометрии применяется аппарат бесконечно-малых и т.д. Это комментарий позволяет установить более тесные контактные связи между различными дисциплинами, способствует расширению, углублению геометрического знания и упрочнению мыслительных операций. Как справедливо заметил Декарт: «Метод состоит в упорядочивании того, на что должен быть направлено острие ума в целях открытия какой-либо истины».

Заметим, что современное развитие науки характерно стремлением к выделению систем изучаемых объектов, когда изучаемые элементы системы образуют некоторое множество абстрактных объектов и явлений реального мира, объединённых наличием между ними широких взаимосвязей, в силу которых порой, исследование свойств отдельного взятого объекта, системы становится затруднительным.

Конструирование –  это одна из подсистем отраслей промышленности, это многопараметрическая система, поэтому влияние одних параметров на другие, их взаимосвязанность может составлять содержание важных научно-исследовательских работ, в которых методы оптимизации выбора параметров естественным образом вливаются в системы автоматизации. В то время как выделение системы приводит к объединению в единое множество различных взаимосвязанных объектов, процессов, явлений, моделирование представляет собой процесс воспроизведения одного отдельно взятого объекта или группы объектов. Модель объекта строится так, чтобы она являлась его аналогом. Наиболее распространёнными являются физические, математические, химические модели.

Параллельно с физическими моделями в процессах в процессах познания природы создаются математические модели. В отличие от физической модели математическая модель не имеет природу, соответствующую природе моделируемого объекта. Также модель включает в себя абстрактные объекты и предложения, описывающие отношения между ними. Функционирование математической модели определяется теми же уравнениями, которые описывают отношения, взаимосвязи между моделируемыми объектами. Одно из определений математической модели звучит так: «Если некоторая математическая система определяется некоторой системой аксиом, то любая система объектов, удовлетворяющая этим аксиомам, считается моделью абстрактной системы». Например, моделью линейного трёхмерного пространства является совокупность векторов, рассматриваемая как классы эквивалентно-ориентированных отрезков.

Наиболее ранними по времени возникновения и наиболее полными для определяемого уровня развития человечества явились модели действительных чисел и евклидовой геометрии. Модели эти создавались и уточнялись в течении тысячелетней практики человечества. Они послужили базой для развития новых боле сложных математических моделей. Вот некоторые из них: модели с одной определяющей операцией (теория абстрактных групп); модели с двумя определяющими операциями (кольца, поля); абстрактные пространства с различной аксиоматикой и различной метрикой модели, допускающие определение предельных процессов (топологические пространства) и многие другие, вплоть до алгебры логики, оперирующей символами высказываний и символами операций. Нельзя обойти вниманием и кибернетические модели, представляющие собой синтез физических и математических моделей с их системами уравнений. Примерами таких моделей являются роботы. Это по мнению академика И.И. Артоболевского признак XXI века.

Остановимся на определении моделей (вторичные модели). Их появление связано с необходимостью построения новых моделей, моделирующих в свою очередь ранее созданные модели. Главным требованием к создаваемых вторичным моделям является однозначность отображения в них основных взаимосвязей между объектами исходных моделей. Так одна и та же математическая модель может иметь несколько вторичных моделей. Например, модель евклидова пространства в качестве вторичных моделей имеет широко известные координатную модель и графическую в виде эпюра Монжа. Вторичными моделями аффинного пространства могут служить модели линейного пространства. Вырожденные линейные преобразования порождают линейную и параллельную аксонометрию как модели аффинного пространства.

В начертательной геометрии получено большое количество проекционных и не проекционных методов графического отображения геометрических фигур: метод двух изображений; двух следов; метод Монжа; полярные методы; аксонометрические методы перспектив и т.д. Все они рассчитаны на графическое отображение какого-нибудь одного из абстрактных пространств: евклидово, аффинного, проективного, коевклидова, неевклидова и т.д.

Конструктивная геометрия – это раздел геометрии, в котором изучаются методы и теория геометрических построений. Некоторые специалисты (Массачусетский Технологический Институт) предлагают включить в конструктивную геометрию номографию, начертательную геометрию черчение, теорию графов и графические методы исследования процессов.

Совокупность всех этих графических дисциплин предлагается назвать «графической геометрией». Можно дать иное определение – прикладной геометрией. Прикладная геометрия – это синтетическая наука, занимающаяся разработкой кибернетических моделей и решающая инженерно-геометрические задачи конструирования и технологии. Прикладная геометрия разрабатывает различные системы алгоритмов как основу для автоматического проектирования различных объектов и их взаимосвязей.

Благотворное влияние аппарата дифференциальной и вычислительной геометрии привело к модернизированным способам конструирования поверхностей, определению геодезических линий на них, построению разного рода намоток, установлению метрических свойств на поверхностях любого вида. Так, если поверхность задана в векторно-скалярной форме r=r(φ) или ,  где  – единичные векторы, то практически можно определить метрику поверхности и её кривизну. В этом случае построив внутреннюю геометрию поверхности можно решать сложные задачи развёрток поверхностей и т.д.

Пусть   или   (1) . Векторы r_u, r_v и, следовательно, их скалярные произведения, есть функции от u и v , поэтому они зависят только от выбора (положения) точки М(u,v). Введём сокращённые обозначения, предложенные К. Гауссом, . Теперь формула (1) может быть представлена в виде  (1). Выражение в правой части называется первой основной квадратичной формой  поверхности. Это соотношение позволяет определять длины дуг кривых на поверхности, т.е. . Этот небольшой комментарий свидетельствует о важности применения дифференциальной геометрии в прикладной геометрии поверхностей.

В настоящее время начертательная геометрия, благодаря высокому уровню мотивации продолжения научных исследований и их технической востребованности, стала надёжным научным аппаратом, с помощью которого решаются сложнейшие прикладные задачи в различных областях науки и техники. Вместе с тем разрабатываются и новые способы модернизации проекционных методов. К развитию и применению методов прикладной геометрии можно с полным основанием применить замечательную мысль выдающегося физика прошлого века Вернера Гейзенберга: «Интеллектуальная сила науки заключается в особенном способе обобщения, позволяющем охватить единым взором разнородные явления и давать этим явлениям единое объяснение».

Говоря о возможности внедрения в классическое содержание  смежных геометрических дисциплин, считаем целесообразным провести исследование поверхностей общего вида визуальными гомографическими методами. Итак, пусть такая поверхность определяется неявным уравнением F(x,y,z)=0 . Это естественно произвольная криволинейная поверхность. Нас интересует поведение кривизны в различных (не особых) точках поверхности. Для любой такой точки поверхности радиусы кривизны нормальных сечений по главным направлениям индикатрисы Дюпена удовлетворяют уравнению Эйлера  или . Это уравнение по своей аналитической структуре с точки зрения номографии принадлежит к канонической форме Коши с бинарным полем.

Литература

1. Курдюмов В.И. Курс начертательной геометрии. Ортогональные проекции. – СПб, 1985.
2. Иванов Г.С., Жирных Б.Г. Геометрическое обеспечение построения гладких сопряжений из отсеков конических поверхностей второго порядка // Инженерный вестник. – 2015. – № 6. – С. 20.
3. Иванов Г.С. Конструктивный способ исследования свойств параметрически заданных кривых // Геометрия и графика. – 2014. – Т. 2. – № 3. – С. 3–6.
4. Нартова Л.Г., Гузненков В.Н. Идеи и методы прикладной геометрии и их применение в технике // Международный научно-исследовательский журнал. – 2015. – № 8-2. – С. 46–50.
5. Гузненков В.Н. Геометро-графическое образование в техническом университете // Alma mater (Вестник высшей школы). – 2014. – № 10. – С. 71–75.
6. Серегин В.И., Иванов Г.С., Боровиков И.Ф., Сенченкова Л.С. Геометрические преобразования в начертательной геометрии и инженерной графике // Геометрия и графика. – 2015. – Т. 3. – № 2. – С. 23–28.
7. Гузненков В.Н., Якунин В.И. Геометро-графическая подготовка как интегрирующий фактор образовательного процесса // Образование и общество. – 2014. – № 2. – С. 26–28.
8. Серегин В.И., Иванов Г.С., Дмитриева И.М., Муравьев К.А. Междисциплинарные связи начертательной геометрии и смежных разделов высшей математики // Геометрия и графика. – 2013. – Т. 1. – № 3-4. – С. 8–12.
9. Гузненков В.Н. Формирование геометро-графического образования в техническом университете: монография. – Москва: Издательство МГТУ им. Н.Э. Баумана, 2014. – 226 с.
10. Якунин В.И., Гузненков В.Н. Геометрическое моделирование как обобщение методов прикладной геометрии и ее разделов // Интеграл. – 2012. – № 5. – С. 120–121.
11. Гузненков В.Н., Журбенко П.А. Модель как ключевое понятие геометро-графической подготовки // Alma mater (Вестник высшей школы). – 2013. – № 4. – С. 82–87.
12. Боровиков И.Ф., Иванов Г.С. Геометрические преобразования в инженерной геометрии // Наука и образование: научное издание МГТУ им. Н.Э, Баумана, 2015. – № 5. – С. 334–347.
13. Иванов Г.С., Дмитриева И.М. Интегрированный курс геометрии и линейной алгебры как средство формирования математической подготовки студентов технических вузов // Омский научный вестник. – 2010. – № 5 (91). – С. 205–208.
14. Иванов Г.С., Дмитриева И.М. О задачах начертательной геометрии с мнимыми решениями // Геометрия и графика. – 2015. – Т. 3. – № 2. – С. 3–8.
15. Якунин В.И., Гузненков В.Н., Журбенко П.А. Геометрическое моделирование как междисциплинарный язык // Дискуссия. – 2012. – № 12. – С. 161–166.
16. Иванов Г.С., Дмитриева И.М. К выбору посредника при решении первой позиционной задачи // Геометрия и графика. – 2015. – Т. 3. – № 1. – С. 26–30.

References

1. Kurdjumov V.I. Kurs nachertatel'noj geometrii. Ortogonal'nye proekcii. – SPb, 1985.
2. Ivanov G.S., Zhirnyh B.G. Geometricheskoe obespechenie postroenija gladkih soprjazhenij iz otsekov konicheskih poverhnostej vtorogo porjadka // Inzhenernyj vestnik. – 2015. – № 6. – S. 20.
3. Ivanov G.S. Konstruktivnyj sposob issledovanija svojstv parametricheski zadannyh krivyh // Geometrija i grafika. – 2014. – T. 2. – № 3. – S. 3–6.
4. Nartova L.G., Guznenkov V.N. Idei i metody prikladnoj geometrii i ih primenenie v tehnike // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal. – 2015. – № 8-2. – S. 46–50.
5. Guznenkov V.N. Geometro-graficheskoe obrazovanie v tehnicheskom universitete // Alma mater (Vestnik vysshej shkoly). – 2014. – № 10. – S. 71–75.
6. Seregin V.I., Ivanov G.S., Borovikov I.F., Senchenkova L.S. Geometricheskie preobrazovanija v nachertatel'noj geometrii i inzhenernoj grafike // Geometrija i grafika. – 2015. – T. 3. – № 2. – S. 23–28.
7. Guznenkov V.N., Jakunin V.I. Geometro-graficheskaja podgotovka kak integrirujushhij faktor obrazovatel'nogo processa // Obrazovanie i obshhestvo. – 2014. – № 2. – S. 26–28.
8. Seregin V.I., Ivanov G.S., Dmitrieva I.M., Murav'ev K.A. Mezhdisciplinarnye svjazi nachertatel'noj geometrii i smezhnyh razdelov vysshej matematiki // Geometrija i grafika. – 2013. – T. 1. – № 3-4. – S. 8–12.
9. Guznenkov V.N. Formirovanie geometro-graficheskogo obrazovanija v tehnicheskom universitete: monografija. – Moskva: Izdatel'stvo MGTU im. N.Je. Baumana, 2014. – 226 s.
10. Jakunin V.I., Guznenkov V.N. Geometricheskoe modelirovanie kak obobshhenie metodov prikladnoj geometrii i ee razdelov // Integral. – 2012. – № 5. – S. 120–121.
11. Guznenkov V.N., Zhurbenko P.A. Model' kak kljuchevoe ponjatie geometro-graficheskoj podgotovki // Alma mater (Vestnik vysshej shkoly). – 2013. – № 4. – S. 82–87.
12. Borovikov I.F., Ivanov G.S. Geometricheskie preobrazovanija v inzhenernoj geometrii // Nauka i obrazovanie: nauchnoe izdanie MGTU im. N.Je, Baumana, 2015. – № 5. – S. 334–347.
13. Ivanov G.S., Dmitrieva I.M. Integrirovannyj kurs geometrii i linejnoj algebry kak sredstvo formirovanija matematicheskoj podgotovki studentov tehnicheskih vuzov // Omskij nauchnyj vestnik. – 2010. – № 5 (91). – S. 205–208.
14. Ivanov G.S., Dmitrieva I.M. O zadachah nachertatel'noj geometrii s mnimymi reshenijami // Geometrija i grafika. – 2015. – T. 3. – № 2. – S. 3–8.
15. Jakunin V.I., Guznenkov V.N., Zhurbenko P.A. Geometricheskoe modelirovanie kak mezhdisciplinarnyj jazyk // Diskussija. – 2012. – № 12. – S. 161–166.
16. Ivanov G.S., Dmitrieva I.M. K vyboru posrednika pri reshenii pervoj pozicionnoj zadachi // Geometrija i grafika. – 2015. – T. 3. – № 1. – S. 26–30.