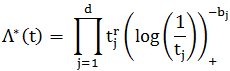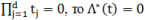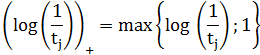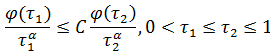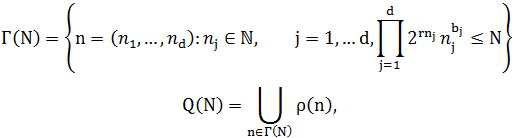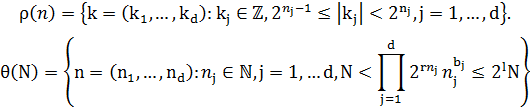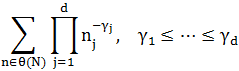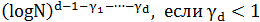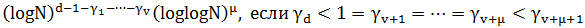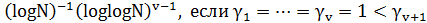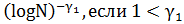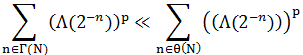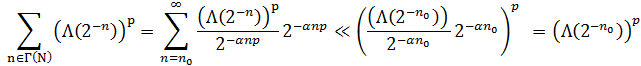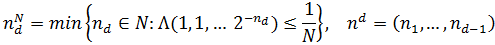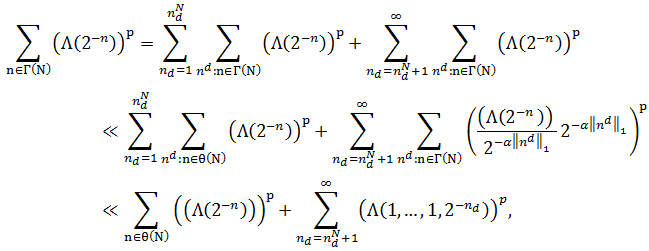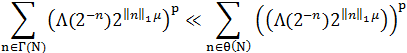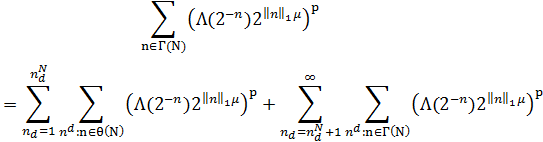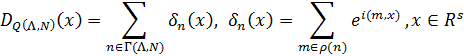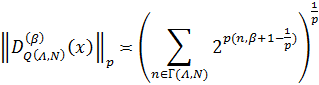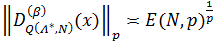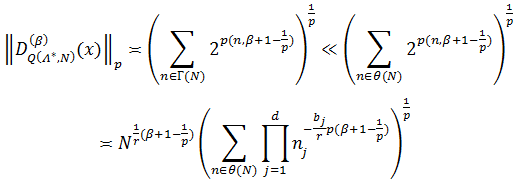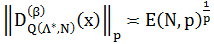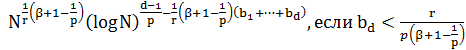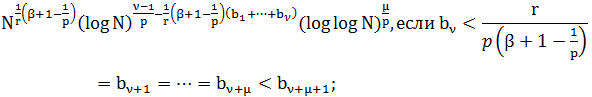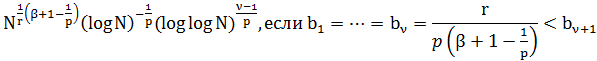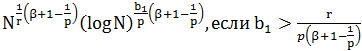ОЦЕНКА НОРМЫ ПРОИЗВОДНЫХ Λ-ЯДЕР ДИРИХЛЕ
Шаянбаева Ш.О.
Магистрант, Казахский Национальный Университет им. Аль-Фараби
ОЦЕНКА НОРМЫ ПРОИЗВОДНЫХ Λ-ЯДЕР ДИРИХЛЕ
Аннотация
В статье установлены оценки норм производных Λ-ядер Дирихле DQ(Λ,N)в Lp, когда спектр приближающих полиномов лежит в множествах типа гиперболических крестов.
Ключевые слова: многомерное ядро Дирихле с произвольным спектром, (r,α)-производная функции, гиперболические кресты.
Shayanbayeva S.О.
Postgraduate student, Al-Farabi Kazakh National University
ESTIMATION OF NORMS OF DERIVATIVES OF DIRICHLET Λ -KERNELS
Abstract
The article describes the process of getting estimations of norms of derivatives of Dirichlet Λ-kernels for DQ(Λ,N) in Lp by when the spectrum lies in approximating polynomials sets the type of hyperbolic crosses.
Keywords: multi-dimensional Dirichlet kernel with an arbitrary spectrum, (r,α)-derivative of function, hyperbolic crosses.
Пусть Λ(t)=Λ(t1,... , td) непрерывная, неубывающая по каждой переменной на [0,1]s функция такая, что Λ(t) > 0 и Λ(t) = 0, смотря по тому 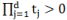 или
или 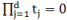 .
.
Пусть даны числа r>0 и bj (j=1,...,d).
Для t=(t1,...,td), tj>0, j=1,...,d, определим функцию Λ*(t) следующим образом: если tj>0, j=1,...,d, то
Далее, не уменьшая, общности можем считать, что b1≤...≤bd.
Функция одной переменной φ(τ)≥0 удовлетворяет условию (Sα), если φ(τ)/τα почти возрастает при некотором 0<α<1, т.е. найдется число C>0, не зависящее от τ1 и τ2, такое, что
Также вводится условие (S) на φ(t) как выполнение условия (Sα) для некоторого α, 0<α<1, и в этом смысле (S)=U0<α<1(Sα).
Будем говорить, что функция Λ(t)= Λ(t1,…,td) удовлетворяет условиям (Sα) при α=(α1,…,αd) если при каждом j=1,...,d функция Λ(t) удовлетрворяет условию (Sαj) по переменной tj при фиксированных остальных.
Легко заметить, что заданная функция Λ*(t) удовлетворяет условию (Sα) при r>α и ∀bj∈R для некоторого α>0
Введем следующие множества (N – множество целых положительных чисел, Z–множество целых чисел)
где
для некоторого l∈N легко заметить что θ(N)=Γ(21N)\Γ(N)
Также ниже мы будем пользоваться обозначениями 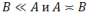 . При положительных A и В запись B<<A будет означать B≤C(α,β,…)·A, где C(α,β,…) некоторые положительные постоянные, зависящие лишь от указанных в скобках параметров, а запись
. При положительных A и В запись B<<A будет означать B≤C(α,β,…)·A, где C(α,β,…) некоторые положительные постоянные, зависящие лишь от указанных в скобках параметров, а запись 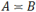 означает что A<<B<<A. Вообще говоря, всюду ниже параметры α,β,… однозначно определяются по смыслу утверждений, поэтому в целях сокращения записей, их указывать не будем.
означает что A<<B<<A. Вообще говоря, всюду ниже параметры α,β,… однозначно определяются по смыслу утверждений, поэтому в целях сокращения записей, их указывать не будем.
Для доказательства основного результата данной работы, нам понадобятся следующие вспомогательные результаты.
Лемма 1. (см. [1]) Сумма
по порядку равна:
Лемма 2. (см. [2]) Пусть функция типа смешанного модуля непрервности порядка l Λ(t)= Λ(t1,…,td) удовлетворяет условию (Sα). Тогда для 0<p<∞ справедлива оценка
Доказательство: применим индукцию по размерности d. При d=1 по свойству (S) имеем
Где n0 - наименьшее натуральное число, при котором Λ(2-n0)<1/N. Предположим, что оценка (3) верная для размерности d-1. Докажем ее для размерности d. Положим
Тогда (к первой сумме применим предположение индукции, а ко второй сумме – свойство (Sα)).
откуда, в силу одномерного случая, получаем утверждение леммы 2.
Лемма 3. (см. [2]) Пусть Λ(t) удовлетворяет условию (Sα) при 0<α<1 таком, что 0<μ <α. Тогда при 0<p<∞ справедлива оценка
Доказательство: как и в лемме 2, применим индукцию по размерности. При d=1 имеем
Применяя к первой сумме предположение индукции, а ко второй сумме условие (Sα), получаем леммы 3.
Положим
Функция DQ(Λ,N)(x) называется многомерным Λ-ядром Дирихле (см., например,[3]).
Теорема 1 (см.[3]). Пусть 1<p<∞ , β∈Rs . Тогда
где 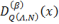 – β-производная функции DQ(Λ,N)(x)
– β-производная функции DQ(Λ,N)(x)
В работе нами доказана следующая теорема.
Теорема 2. Пусть 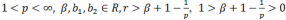 . Тогда справедлива следующая оценка
. Тогда справедлива следующая оценка
Доказательство. Используя утверждения теоремы 1 и леммы 3, получим
Далее применяя лемму 1, в случае когда 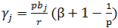 , получаем
, получаем
Где E(N,p) – величина по порядку равна:
Таким образом, теорема доказана.
Литература
- Пустовойтов Н. Н. О приближение периодических функций из классов линейными методами // Математический сборник, 2012. Том 203. №1. С.99-114.
- Пустовойтов Н. Н. Приближение многомерных функций с заданной мажорантой смешанных модулей непрерывности // Математические заметки. 1999. Т 65. №1. С.107-117.
- Сихов М.Б. Неравенства типа Бернштейна, Джексона-Никольского и оценки норм производных ядер Дирихле // Матем.заметки, 2006, Т.80, вып.1, с.95-104.
- Сихов М. Б. О некоторых задачах многомерной теории приближений разных метрик // Докторская диссертация на соискание степени доктора физико-математических наук. Казань, 2010. 186 с.
- Сихов М.Б. Об оценках норм производных ядра Дирихле с гармониками // Известия НАН РК. Сер. физико-математическая , 2003, №1, с.57-62
References
- Pustovojtov N. N. O priblizhenii periodicheskih funkcij iz klassov lineynimi metodami// Matematicheskij sbornik. 2012. T 203. №1. S.99-114.
- Pustovojtov N. N. Priblizhenie mnogomernyh funkcij s zadannoj mazhorantoj smeshannyh modulej nepreryvnosti // Matematicheskie zametki. 1999. T 65. №1. S.107-117.
- Sikhov M.B. Neravenstva tipa Bernshtejna, Djeksona-Nikolskogo I ocenki norm proizvodnyh yader Dirikhle // Matem.zametki, 2006, T.80, vip.1, s.95 – 104.
- Sikhov M. B. O nekotoryh zadachah mnogomernoj teorii priblizhenij raznyh metrik // Doktorskaja dissertacija na soiskanie stepeni doktora fiziko-matematicheskih nauk. Kazan’, 2010. 186 s.
- Sikhov M.B. Ob ocenkah norm proizvodnyh yadra Dirikhle s garmonikami // Izvestiya NAN RK . ser. Fiziko-matematicheskaya, 2003, №1, s.57-62.