СИММЕТРИИ И ТОЧНЫЕ РЕШЕНИЯ МУЛЬТИПЛИКАТИВНОГО КЛАССА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ЭКСПОНЕНЦИАЛЬНЫМИ ФУНКЦИЯМИ
СИММЕТРИИ И ТОЧНЫЕ РЕШЕНИЯ МУЛЬТИПЛИКАТИВНОГО КЛАССА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ЭКСПОНЕНЦИАЛЬНЫМИ ФУНКЦИЯМИ
Аннотация
В данной статье исследуются дискретные симметрии класса обыкновенных дифференциальных уравнений 2-го порядка с мультипликативными правыми частями.
Найдены дискретные преобразования, замкнутые в рассматриваемом классе уравнений. Построена дискретная группа преобразований и её граф. Получены все элементы орбиты исходного мультипликативного уравнения, содержащего экспоненциальную функцию.
Приведен способ поиска точных решений уравнений указанной орбиты при некоторых значениях параметров, входящих в уравнения. Рассмотрены примеры нахождения решений уравнений этой орбиты.
В работе использован метод расширения класса уравнений, а также метод «размножения» разрешимых случаев в исследуемом классе уравнений, основанный на том факте, что решения уравнений связаны теми же преобразованиями, что и сами уравнения.
1. Введение
Дискретно-групповой анализ обыкновенных дифференциальных уравнений (ДГА ОДУ) был разработан В. Ф. Зайцевым в конце 20-го века. Он открыл дискретные группы преобразований дифференциальных уравнений.
Основой ДГА ОДУ является поиск преобразований, замкнутых в исследуемом классе уравнений. (До В. Ф. Зайцева были известны лишь простейшие из таких преобразований, например ,
и т.д.) Важным приложением ДГА ОДУ является алгоритмизированный поиск их точных решений.
Первая наиболее полная работа, в которой изложены основы ДГА ОДУ и приведены точные решения сотен новых разрешимых уравнений, полученных В. Ф. Зайцевым, его коллегой А. Д. Поляниным и их научными школами – это справочник-монография (в эту же книгу вошли, в частности, основные теоретические и практические результаты кандидатской диссертации автора данной статьи).
В последующих справочниках-монографиях этих же авторов содержатся точные решения уже тысяч новых интегрируемых уравнений, найденных методом «размножения» по дискретным группам (см. далее).
К сожалению, в настоящее время дискретным группам преобразований ОДУ математическим сообществом уделяется незаслуженно мало внимания: считанное число математиков занимается исследованием ОДУ с помощью дискретных групп преобразований. Большинство «групповиков» занимаются непрерывными группами преобразований, причём в основном, для уравнений с частными производными.
Данной статьёй, так же как и прошлыми работами
, и т.д., автор пытается ликвидировать этот пробел в теории дифференциальных уравнений.В данной работе рассматриваются дискретные симметрии мультипликативного класса обыкновенных дифференциальных уравнений (ОДУ) 2-го порядка:
Исследование симметрий этого класса уравнений было начато В. Ф. Зайцевым с подкласса (1) при
причём, со случая степенных функций K, L, M:
(класс уравнений (3) называется классом обобщённых уравнений Эмдена-Фаулера).
В работах
, , , , класс степенных уравнений (3) был расширен:– для достижения замкнутости некоторых дискретных преобразований.
В статьях
, , было начато исследование дискретных симметрий класса уравнений (1) с произвольными функциями, а также были рассмотрены некоторые спецификации, в частности, уравнение свободных колебаний маятника. В данной статье исследуется ещё одна спецификация: уравнения классов (1) и (2) содержат экспоненциальные функции.Наличие дискретной группы преобразований, замкнутых в рассматриваемом классе уравнений, позволяет находить новые разрешимые случаи в этом классе уравнений с помощью метода «размножения» по данной дискретной группе: если известно решение, частное или общее, хотя бы одного уравнения, соответствующего некоторой вершине графа группы, то с помощью преобразований данной дискретной группы можно получить решения всех остальных уравнений, соответствующих остальным вершинам графа.
В статье используются, в частности, следующие термины: дискретная группа преобразований, порождающий (образующий) элемент и определяющие соотношения дискретной группы, код дискретной группы, группа диэдра и т.д., с определениями которых можно ознакомиться в работах
, .2. Применение группы к классу уравнений с экспонентой
Для класса уравнений (1) с произвольными функциями была построена
, , группа диэдра D6 12-го порядка – группа преобразований, замкнутых в (1):(E – тождественное преобразование), где r и h – образующие группы (5);
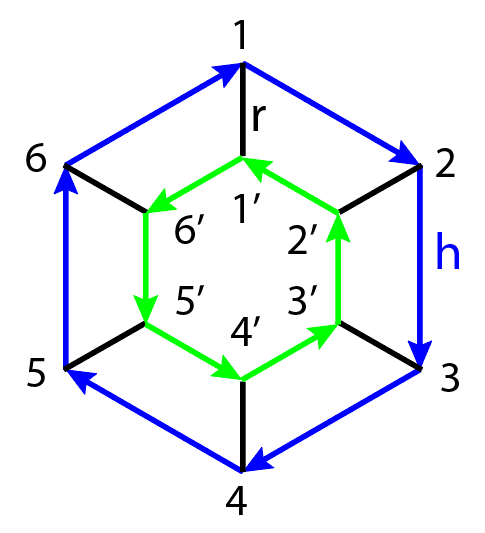
Рисунок 1 - Граф группы D6
Таблица 1 - Уравнения-вершины графа на рис. 1
Примечание: вершина 1 соответствует (8)
3. Применение группы D3 к (8)
Для класса уравнений (2) была построена , группа диэдра D3 преобразований, замкнутых в (2):
где r и g – образующие дискретной группы D3;
(показатель «-1» в (11) означает обратную функцию).
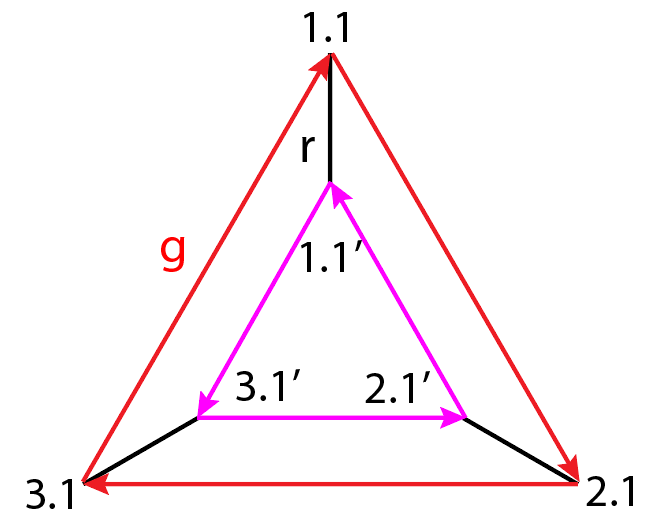
Рисунок 2 - Граф группы D3
Таблица 2 - Уравнения-вершины графа на рис. 2
Примечание: вершина 1.1 обозначает (12)
Преобразование g зависит от функций K, L, M преобразуемого уравнения, поэтому при каждом следующем применении уравнение g имеет другой вид.
С помощью (11) можно вычислить преобразование g на каждом шаге:
Так как преобразования g и r замкнуты в классе уравнений (2), то все уравнения таблицы 2 имеют вид (2).
Удивительным фактом является то обстоятельство, что только уравнения 1.1 и 1.1’ содержат экспоненты. Остальные 4 уравнения являются степенными. Уравнения 1.1 и 1.1’ являются сингулярными элементами степенного класса уравнений (3), соответствующими в (3) случаям k=∞ и l=∞ для 1.1’.
4. Применение дискретной группы 36-го порядка к (12)
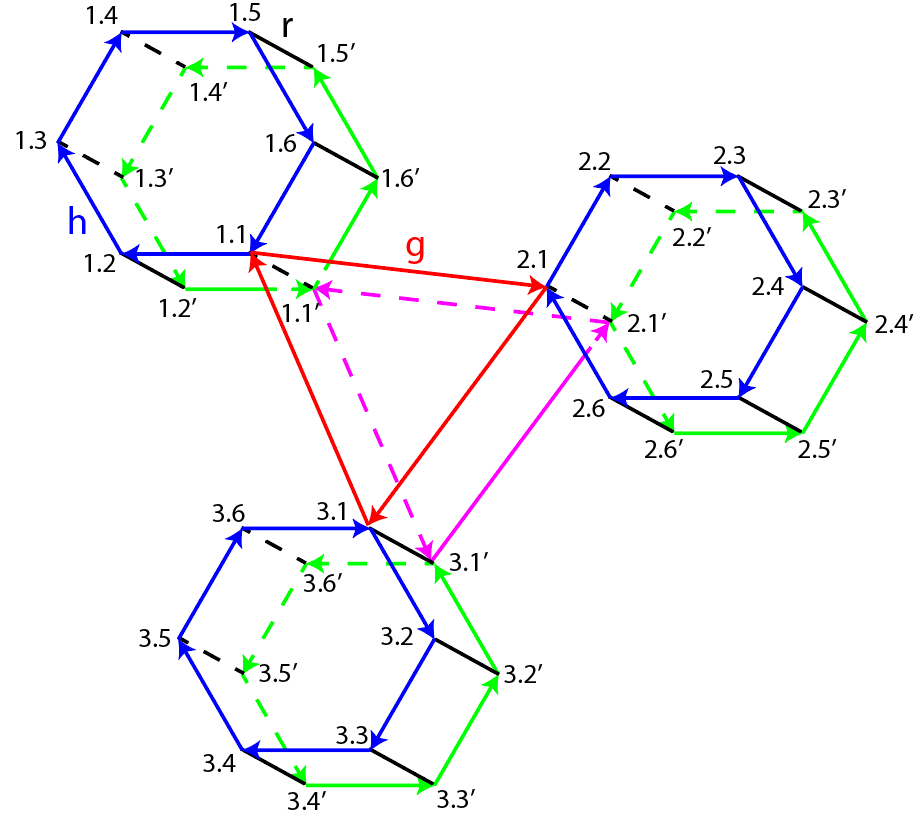
Рисунок 3 - Граф группы 36-го порядка
Таблица 3 - Уравнения-вершины графа на рис. 3
Примечание: вершина 1.1 обозначает (12)
5. Нахождение точных решений уравнений орбиты (12)
Если одно из уравнений таблиц 1, 2, 3 при некоторых значениях параметров является интегрируемым, то это же можно сказать обо всех остальных уравнениях в этих таблицах. Метод «размножения» разрешимых случаев в рассматриваемых классах уравнений основан на том, что преобразования дискретных групп (здесь 6-го, 12-го и 36-го порядков), связывающие уравнения, связывают и их решения. Кроме того, если решение исходного уравнения выражается через некоторые элементарные или специальные функции, то и решения уравнений его орбиты (здесь остальных уравнений таблиц 1, 2, 3) выражаются через эти же функции. Указанные выше преобразования легко установить по графам на рис. 1, 2, 3 – они являются композициями образующих g, h, r.
С помощью метода «размножения» известный справочник Камке по ОДУ был значительно расширен: единичные разрешимые случаи различных классов уравнений были «размножены» до десятков и сотен
, , , .Пример 1. Рассмотрим уравнение (12) при ,
:
оно имеет номер 1.1 на рис. 1 и в таблице 1.
Его общее решение в параметрическом виде
:Найдём, к примеру, решение уравнения 1.3’:
Согласно рис. 3, уравнение 1.3’ (15) приводится к уравнению 1.1 (13) преобразованием h2r; с помощью (6) и (7) его легко вычислить:
Композиция (16) и (14) является общим решением уравнения 1.3’ (15):
.
Пример 2. Аналогично вычислим решение, например, уравнения 1.2’:
Это немного сложнее, так как уравнение 1.2’ (17) приводится к уравнению 1.1 (13) не с помощью точечного преобразования, а с помощью касательного преобразования:
Заметим, что преобразование hr оказалось известным касательным преобразованием Лежандра, в котором x и y зависят от производной. Дополнительно необходимо в решении (14) уравнения 1.1 (13) вычислить и
:
Таким образом, композиция преобразования hr (18) и общего решения (14, 19) уравнения 1.1 (13) является общим решением уравнения 1.2’ (17):
Замечание. С помощью операции масштабирования можно вычислить решения всех уравнений орбиты исходного уравнения (13) с произвольными коэффициентами в правых частях.
6. Заключение
Обыкновенные дифференциальные уравнения нередко возникают в различных разделах естествознания, особенно при решении уравнений математической физики и механики
, .В данной статье дискретные группы преобразований 6-го, 12-го и 36-го порядков применены к мультипликативному классу ОДУ 2-го порядка, содержащему в правой части степенные и экспоненциальный сомножители.
Найдена орбита исходного дифференциального уравнения, состоящая из 36-ти мультипликативных уравнений, содержащих в правых частях экспоненциальные функции. Приведён метод «размножения» разрешимых случаев исходного дифференциального уравнения: если при некоторых параметрах исходное уравнение интегрируется, то интегрируются также все уравнения его орбиты, причём их решения выражаются через те же функции, что и решение исходного уравнения.
Рассмотрены примеры, иллюстрирующие получение точных решений уравнений, содержащих экспоненциальные функции, через решение исходного дифференциального уравнения.
В дальнейшем можно в (12) рассмотреть ekx вместо ex, а также расширить дискретную группу 36-го порядка для интегрируемых подклассов класса уравнений (12).
