DL-МОДЕЛЬ RFR ДЛЯ ФИНАНСОВОГО МЕНЕДЖМЕНТА БИРЖЕВЫМ АКТИВОМ SIM3 НА MOEX

Проблема совершенствования подходов в использовании цифровых решений в сфере финансового менеджмента приводит к необходимости применения моделей торговых советников (rob-эдвайзеров), биржевых роботов. Повышение точности прогнозирования остается актуальной проблемой, несмотря на широкомасштабное применение алгоритмической торговли в мире и на Московской бирже, в частности.

Научная новизна состоит в том, что в отличие от большинства алгоритмов, применяемых систем искусственного интеллекта, авторами предложено использование модели глубокого обучения «Случайный лес» в качестве биржевого торгового эдвайзера.

Как известно «Случайным лесом» называется метод ансамблевого обучения, который способен выполнять

1) классификацию,

2) регрессию с помощью ансамбля деревьев решений.

Известно, что если агрегируются прогнозы группы предикторов (классификаторы, регрессоры), то частым результатом будет получение лучших прогнозов, нежели с индивидуальным предиктором. Группа предикторов называется ансамблем; таким образом, этот метод называется ансамблевым обучением. К преимуществу «Случайного леса» относят тот факт, что он имеет меньшую ошибку обобщения, чем одиночные деревья решений, из-за его случайности, которая уменьшает дисперсию модели

По мнению ряда экспертов, существует определенная связь между алгоритмической торговлей, активностью частных инвесторов на бирже и стабильностью развития финансового сектора экономики. Проблемы, связанные с финансовой стабильностью, были предметом изучения значительного количества западных ученых. Среди них: Джон Чант. Эндрю Крокет, Внм Дуйзенберг, Роджер Фергюсон, Майкл Фут, Сэр Эндрю Лардж, Фредерик Мишкин. Гарри Шинаси и другие.

По мнению ученых Хенгхи (Hengxu), Донг (Dong), Вейквинг (Weiqing) и Джиан (Jiang), нет единой концепции финансовой стабильности ни в российской, ни в зарубежной науке

Представляется целесообразным для эффективной спекулятивной торговли использовать такой математический аппарат, как случайный лес, важнейшим элементом которого является дерево решений. Деревья решений (DT) основаны на непараметрическом методе обучения с учителем, который используется для классификации и регрессии.

Целью метода является создание модели, предсказывающей значение целевой переменной на основе изучения простых правил принятия решений, которые выводятся из характеристик данных. Дерево можно рассматривать как кусочно-постоянную аппроксимацию. Чем глубже дерево, тем сложнее правила принятия решений и тем точнее модель. Деревья решений используются как для задач классификации, так и для задач регрессии. Понимание важности переменных в лесах случайных деревьев представлено во многих работах, в том числе Louppe G. и других

Среди современных трендов применения систем искусственного следует отметить следующие тренды. Ритеш Кумар Дубей (Ritesh Kumar Dubey) c коллегами изучая вопросы эффективности алгоритмической торговли и ее влияние на качество рынка, пришел к выводу, что алгоритмическая торговля (АТ) была презираема розничными трейдерами и регуляторами рынка за ее скорость, поскольку приводит к непреднамеренной волатильности

Автор Мэтью Ф. Диксон (Matthew F. Dixon) с коллегами ввели фундаментальные концепции машинного обучения для канонического моделирования и рамок принятия решений в области финансов. Представили примеры, упражнения и коды Python для закрепления теоретических концепций и демонстрации применения машинного обучения к алгоритмической торговле, управлению инвестициями, управлению капиталом и управлению рисками

Любопытным направлением выступает управление таким инвестиционным активом, как NFT. Аббревиатура NFT образована от английского «non-fungible token», что в переводе означает «невзаимозаменяемый токен». По мнению Трубчаниновой К.А. и Коноваловой М.Е., он представляет собой особый вид криптографической учетного сертификата (токена), который является уникальным и не может быть уничтожен, обменен или замещен другим токеном

Колоссальные изменения наблюдаются в финансовой сфере, что, по мнению Ванцовской А.А., главным образом, связано с появлением технологии блокчейн и криптовалюты, поскольку эти технологии, помимо того, что открывают новые возможности для инвестирования, кардинально трансформируют разного рода договорные отношения

Исследованию роли систем управления инвестициями при соблюдении нормативных требований, в частности, исследование механизмов вытеснения после финансового кризиса посвятил свои труды Даниэль Гозман (Daniel Gozman) с коллегами

В работе использованы такие методы исследования, как теоретический, аналитический, статистический и система искусственного интеллекта на основе глубокого обучения «метод случайного леса».

Метод случайного леса (англ. random forest) – алгоритм машинного обучения, предложенный Лео Брейманом (Breiman Leo)

В результате проведенного исследования:

1) сформирована DL-модель «случайный лес»;

2) получены прогнозные значения Pc;

3) исследована точность прогнозирования DL-модель «случайный лес» и качество работы модели;

4) выявлены определенные величины гиперпараметров при настройке DL-модели, которые обеспечивают наименьшие ошибки при прогнозировании цены закрытия (Pc) фьючерса SiM3 на следующий таймфрейм;

5) рассчитана средняя доходность при использовании сигналов модели для поддержки принятия управленческих решений инвестора при проведении спекулятивных операций с фьючерсом SiM3.

Во-первых, DL-модель «случайный лес» была успешно сформирована.

Датасет DL-модели «случайный лес» был получен путем экспорта свечей из торгового терминала QUIK (таблица 1).

Для формирования датасета была добавлена колонка «Target» – в которой представлена цена закрытия «close» на следующий тайм-фрейм. Опустим колонку «target» на 1 таймфрейм вниз, чтобы предсказательная цена получилась из последующей (t+1) «Close», заполним появившийся пропук, удалим не полную последнюю строку. Target = цена закрытия на завтра (close на следующий день)

Было сформировано обучающее X-множество и целевое у-множество, проведено обучение модели с использованием библиотеки DecisionTreeRegressor (рисунок 1).

Рисунок 1 - Скрипт для формирования обучающего «X», целевого «у»-множества и обучение модели

Примечание: авторская разработка

DOI:10.23670/IRJ.2023.132.57.2

Последний шаг предварительной обработки – разделение данных на обучающие и тестовые наборы. Библиотека model_selection Scikit-Learn содержит метод train_test_split, который был использован для случайного разделения данных на наборы для обучения и тестирования. DL-модель была успешно сформирована (рисунок 2).

Рисунок 2 - Визуализация «решающего дерева» DL-модели, имеющего 28 уровней

Примечание: авторская разработка

DOI:10.23670/IRJ.2023.132.57.3

Во-вторых, получены прогнозные значения Pc.

В результате использования DL-модели были сформированы прогнозы на тестовом наборе (таблица 2).

В-третьих, исследована точность прогнозирования DL-модели «случайный лес» и качество ее работы с помощью метрик.

Гистограмма распределения величин параметра «Дельта», рассчитанного как разность между фактическим значением цены «Actual» и прогнозным – «Predicted» показывает, что в более чем 250 случаях из 424 отклонение (ошибка прогноза) составляет от 0 до 500 рублей (рисунок 3).

Для оценки производительности алгоритма регрессии обычно используются метрики: средняя абсолютная ошибка, среднеквадратичная ошибка и среднеквадратичная ошибка. Библиотека Scikit-Learn содержит функции, которые обеспечивают вычисление этих значений. Для этого используется требуемый код из пакета метрик.

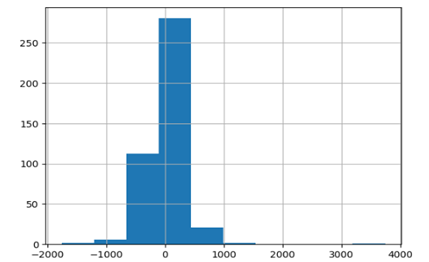
Рисунок 3 - Гистограмма распределения величин параметра «Дельта»

Примечание: авторская разработка

DOI:10.23670/IRJ.2023.132.57.5

Для оценки производительности алгоритма регрессии обычно используются метрики: средняя абсолютная ошибка, среднеквадратичная ошибка и среднеквадратичная ошибка. Библиотека Scikit-Learn содержит функции, которые могут помочь с вычислением этих значений. Для этого используется необходимый код из пакета метрик.

Оценка алгоритма регрессии обычно используются метрики: средняя абсолютная ошибка, среднеквадратичная ошибка и среднеквадратичная ошибка. Библиотека Scikit-Learn содержит функции, которые могут помочь нам вычислить эти значения.

MAE – метрика, которая сообщает нам среднюю абсолютную разницу между прогнозируемыми значениями и фактическими значениями в наборе данных.

(1)

Где: Σ – это символ, который означает «сумма»;

 - наблюдаемое значение для i -го наблюдения;

 - прогнозируемое значение для i -го наблюдения;

n – размер выборки.

Чем ниже MAE, тем лучше модель соответствует набору данных.

Среднеквадратичная ошибка (Mean Squared Error) применяется в случаях, когда требуется подчеркнуть большие ошибки и выбрать модель, которая дает меньше именно больших ошибок. Большие значения ошибок становятся заметнее за счет квадратичной зависимости. MSE рассчитывается по формуле:

(2)

Где: n – количество наблюдений по которым строится модель и количество прогнозов,

- фактические значение зависимой переменной для i-го наблюдения,

- значение зависимой переменной, предсказанное моделью.

Среднеквадратичное отклонение (RMSD) или среднеквадратичная ошибка (RMSE) иначе R2 является часто используемой мерой различий между значениями (значениями выборки или совокупности), предсказанными моделью, и наблюдаемыми значениями. RMSD представляет собой квадратный корень из второго момента выборки различий между прогнозируемыми значениями и наблюдаемыми значениями. Корень из среднеквадратичной ошибки (Root Mean Squared Error) вычисляется просто как квадратный корень из MSE: (3)

(3)

В-четвертых, выявлены определенные величины гиперпараметров при настройке DL-модели, которые обеспечивают наименьшие ошибки при прогнозировании цены закрытия (Pc) фьючерса SiM3 на следующий таймфрейм.

Анализ данных позволяет сделать вывод о высокой точности прогноза, поскольку уровень средней абсолютной ошибки модели не превышает значения 133,52 руб., а уровень MSE при этом составляет 1729,27, при этом RMSE = 41,58 для варианта в котором доля тестовой выборки в датасете составляла 0,20 (таблица 3).

Использование библиотеки GridSearchCV позволило выбрать DL-модель с лучшими параметрами: {'criterion': 'squared_error', 'max_depth': 10, 'n_estimators': 50}. То есть по критерию «'squared_error», с глубиной «'max_depth'» = 10, с количством решающих деревьев - 50.

В-пятых, рассчитана доходность инвестора при использовании сигналов DL-модели для поддержки принятия управленческих решений при проведении спекулятивных операций с одним фьючерсным контрактом SiM3 (таблица 4).

Как показывают исследования, за рассматриваемый период с 16 сентября 2022 г. 15:00 по 07 апреля 2023 г. 23:00 имели место 2124 наблюдений (часовых таймфреймов). Количество наблюдений, вошедших в тестовую выборки составило 424, при этом средняя величина Pactual составила 67918.09 рублей, а Ppredicted составила 67917,73 рублей. Поскольку известно, что среднеквадратическое значение параметра «Delta» – профита инвестора, то при общем количестве наблюдений N=424, расчетное значение совокупного профита составляет 141162,32 рублей = 424*332,93.

Анализируя тенденции развития искусственного интеллекта в сфере финансового менеджмента, важно отметить некоторые аспекты, выявленные зарубежными учеными. Практика показывает, что важное значение имеет оценка финансового риска. В перспективе просматриваются следующие направления исследований.

Представляется целесообразным для эффективной спекулятивной торговли использовать такой математический аппарат, как случайный лес в современных интерпретациях. Ломакин Н.И. с коллегами, исследуя цифровизацию и будущее финансовых услуг, анализируя влияние технологических разработок на финансовый сектор, делает вывод о необходимости широкого применения инноваций в сфере цифровых финансов

Дерево бинарной классификации (соответственно регрессии), предложенное в работе Breiman, представляет собой модель ввода-вывода, представленную древовидной структурой T из случайного входного вектора (X1…Xp), принимающего свои значения в (X1*…*Xp)=X в случайную выходную переменную Y 𝜖 𝛶

Таким образом, на основании вышесказанного можно сделать выводы:

1. Представлен алгоритм управления биржевым активом – фьючерсным контрактом на доллар SiM3 на Московской бирже (MoEx). В основу алгоритма положена модель глубокого обучения «Рандом Форест Регрессия» (DL RFR).

2. Разработанная DL-модель позволяет получать прогноз цены закрытия фьючерсного контракта на следующий таймфрейм – час, что позволяет обеспечить поддержку принятия управленческого решения по поводу покупки/продажи биржевого актива SiM3.

3. Расчеты свидетельствуют о том, что DL-модель показывает высокую точности прогноза, поскольку уровень средней абсолютной ошибки модели не превышает значения 133,52 руб., а уровень MSE при этом составляет 1729,27, при этом RMSE = 41,58 для варианта в котором доля тестовой выборки в датасете составляла 0,20.

4. Применение систем искусственного интеллекта позволяет решать широкий круг проблем, в алгоритмической торговле и обеспечить эффективное управление биржевым активом.