РАЗРАБОТКА ИНТЕЛЛЕКТУАЛЬНОГО ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ ДЛЯ ОБУЧЕНИЯ СТУДЕНТОВ ПРИЁМАМ РАСПАРАЛЛЕЛИВАНИЯ ВЫЧИСЛЕНИЙ

РАЗРАБОТКА ИНТЕЛЛЕКТУАЛЬНОГО ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ ДЛЯ ОБУЧЕНИЯ СТУДЕНТОВ ПРИЁМАМ РАСПАРАЛЛЕЛИВАНИЯ ВЫЧИСЛЕНИЙ

Научная статья

Ступников А.А.¹, Гаврилова Н.М.^2, *

¹ ORCID: 0000-0001-5201-1260;

² ORCID: 0000-0002-8697-5639;

^{1, 2} Тюменский государственный университет, Тюмень, Россия

* Корреспондирующий автор (n.m.gavrilova[at]utmn.ru)

Аннотация

В работе содержится описание подхода к разработке интеллектуального программного обеспечения для выполнения учебных и научных исследований в области распараллеливания вычислений. На примере численного решения уравнения теплопроводности с использованием неявной схемы рассматриваются особенности организации распараллеливания метода трехдиагональной прогонки на многопроцессорной системе с общей памятью. Оценивается время расчета последовательного и параллельного алгоритмов. Приводятся результаты сравнения времени и ускорения при использовании разных алгоритмов распараллеливания и технологий реализации.

Ключевые слова: система линейных алгебраических трехточечных уравнений, метод трехдиагональной прогонки, распараллеливание прогонки, последовательный алгоритм, блочный алгоритм.

DEVELOPMENT OF INTELLECTUAL SOFTWARE TO TRAIN STUDENTS TO COMPUTATE PARALLELLY

Research article

Stupnikov A.A.^1, *, Gavrilova N.M.²

¹ ORCID: 0000-0001-5201-1260;

² ORCID: 0000-0002-8697-5639;

^{1, 2} Tyumen State University, Tyumen, Russia

* Corresponding author (n.m.gavrilova[at]utmn.ru)

Abstract

The paper describes an approach to the development of intelligent software for the implementation of educational and scientific research in the field of computing parallelization. We consider the organization features of parallelization in the tridiagonal sweep method on a multiprocessor system with shared memory using the numerical solution of the heat equation with an implicit scheme as an example. The authors estimate calculation time of sequential and parallel algorithms. The results of comparing time and acceleration using different parallelization algorithms and implementation technologies are presented.

Keywords: system of linear algebraic three-point equations, three-diagonal sweep method, parallel sweep parallelization, sequential algorithm, block algorithm.

Введение

В ходе численного решения задач, моделирующих физические процессы, основное внимание исследователь уделяет выбору подходящих методов решения и грамотной компьютерной реализации этих методов. Вопросы, связанные с визуализацией решения, внедрением результатов решения в другие проекты, повышением эффективности и скорости расчётов, обычно рассматриваются как второстепенные, не значимые для расчета конкретной задачи.

В рамках выполнения научных исследований решения одной задачи чаще всего бывает недостаточно, и исследователю приходится многократно выполнять целый комплекс основных и вспомогательных процедур, затрачивая значительное время на переключения между этапами.

Например, при изучении влияния характера источникового члена в задачах теплопроводности основное внимание уделяется численной реализации. При этом не меньшее время затрачивается на конвертацию полученных результатов в разные форматы как для визуального оценки полученных результатов, так и для дальнейшей обработки в специализированных пакетах с целью получения наглядного изображения исследуемого процесса.  Исследователю приходится многократно повторять указанные шаги, с целью получения обобщающего вывода на основе комплекса исследований, что делает процесс исследования затратным по времени и допускающим ошибки человеческого фактора.

Авторами реализован подход, обеспечивающий соединение этапов научных исследований расчетно-аналитического типа в виде программного комплекса, позволяющего выполнять расчёты, аккумулировать результаты и формировать динамические карты распределения результатов для визуального анализа возникающих ситуаций. Построение подобных динамических карт требует как повышения скорости работы вычислительных устройств, так и одновременного решения на них различных задач.

Подобный подход важен в частности и для других задач, имеющих практический интерес, например, для задач, связанных с распространением загрязнений, для диспетчера, который следит за состоянием температурного режима здания, и т.п. Полученные результаты, в том числе, могут быть использованы для отслеживания, выявления и оповещения о каких-то критических ситуациях, в том числе, чисто визуально.

Методы и принципы исследования

В данной работе рассматривается реализация первого блока этого комплекса, обеспечивающего распараллеливание расчетного алгоритма. Важным фактором реализации является оценка эффективности различных подходов к организации способов распараллеливания вычислительных процессов.

Численное решение краевой задачи для уравнения теплопроводности с использованием неявной конечно-разностной схемы сводится к решению системы линейных алгебраических уравнений, имеющей специальный (трехдиагональный) вид. Для нахождения решения таких систем используется метод прогонки, который реализуется в последовательном режиме. Для требуемого ускорения расчетов при большом объеме начальных данных и высокой требуемой точности вычисления необходимо использовать параллельные алгоритмы для решения СЛАУ с трехдиагональной матрицей коэффициентов при неизвестных.

Так как данная разработка предназначена для использования в образовательном процессе для студентов, изучающих как численное моделирование, так и методы распараллеливания вычислений, были выполнены несколько реализаций распараллеливания алгоритма прогонки на общей памяти средствами OpenMP и с использованием технологии организации параллельных вычислений на основе потоков.

Особенности организации параллельных вычислений с использованием многопроцессорных вычислительных систем рассматриваются в работах [1], [2], [3]. Варианты организации ускорения параллельных расчетов задачи теплопроводности рассматривались разными коллективами авторов. Очевидно, что практический интерес вызывают работы, связанные с реализацией неявной разностной схемы для уравнения теплопроводности с использованием методов распараллеливания трехдиагональной прогонки [6], [7], [9].

Среди различных способов распараллеливания вычислений при решении систем алгебраических уравнений с трехдиагональной матрицей рассматривались алгоритмы, вычислительная практика использования которых достаточно известна: метод встречной прогонки, метод параметрической прогонки (метод Яненко [4]), параллельно-конвейерный метод [6], метод параллельно-циклической редукции, горизонтально-блочный параллельный алгоритм [5].

В данной работе для распараллеливания метода трехдиагональной прогонки рассматривается использование алгоритма встречной прогонки и блочного алгоритма на системах с общей памятью.

Кратко рассмотрим особенности этих подходов для системы линейных уравнений с трехдиагональной матрицей коэффициентов при неизвестных вида:

    (1) Прямой ход метода правой прогонки позволяет вычислить прогоночные коэффициенты по формулам:   (2) По формулам обратного хода правой прогонки вычисляются неизвестные .   (3) Для выполнения левой прогонки расчётные формулы строятся аналогично. Прямой ход:     (4) Обратный ход:     (5)

Алгоритм встречной прогонки подразумевает независимое применение обоих методов, что позволяет одновременно использовать два параллельных потока, реализующих эти методы. Первый из потоков, реализуя метод правой прогонки для уравнений с номерами , вычисляет коэффициенты  по формулам (1) и (2). Вычисление прогоночных коэффициентов (4) метода левой прогонки  для уравнений с номерами  выполняется во втором потоке.

Сопряжение решений обоих потоков в виде (3) и (5) происходит при . Здесь значение , присутствующее в результатах обеих прогонок, находится из системы двух уравнений:

     (6)

Определив значение , можно найти все , при  в первом потоке, и все значения , при   во втором потоке.

Время решения системы последовательным методом прогонки при больших значения размерности системы  определяется как , где τ время выполнения одной операции. При параллельной реализации методом встречной прогонки время работы алгоритма можно оценить, как , где δ – время обслуживания потоков, затрачиваемое при создании и закрытии параллельной секции. В обоих случаях при увеличении размера системы время расчета возрастает линейно, но параллельный алгоритм сокращает время примерно в 2 раза.

Большее ускорение можно получить при использовании для распараллеливания блочного алгоритма [5], позволяющего нагружать расчетами большее число процессоров (потоков p>2).

Алгоритм блочной прогонки осуществляет исключение поддиагональных элементов для каждой полосы размера   строк основной матрицы, т.е. k-й поток обрабатывает строки с номерами  Например, расчеты для матрицы системы размерности n=12 и числе потоков p=3, сводятся к параллельному решению трех систем размерности  m=4.

Поскольку каждая полоса матрицы, соответствующая потоку с номером k, (кроме k=1) содержит по три неизвестных в каждой строке, то после прямого хода в каждой полосе, за исключением первой, появится новый столбец коэффициентов.

Формулы прямого хода алгоритма горизонтально - блочной прогонки позволяют вычислить прогоночные коэффициенты α, β и γ для каждой полосы (потока) размера  по формулам (при p=1 верны формулы правой прогонки (2)):

     (7)

Использование в блочном алгоритме формул обратного хода позволяет в каждом потоке исключить наддиагональные элементы.

Обратный ход метода вычисляет прогоночные коэффициенты m, l, k:

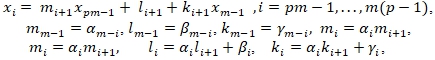    (8) В итоге матрица коэффициентов исходной системы уравнений принимает блочный вид.

Затем, с помощью найденных коэффициентов, формируется система уравнений размера () с трехдиагональной матрицей, состоящая из уравнений на нижних границах каждой полосы вида:

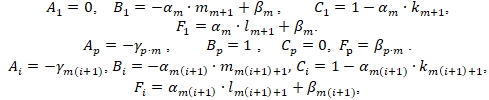с коэффициентами:   (9)

Ее решение находится обычным последовательным методом прогонки.

Далее, с помощью найденных граничных значений неизвестных каждой полосы, остальные неизвестные (внутренние переменные в каждом блоке) находятся по формулам:

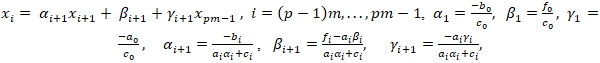    (10) Эти значения опять можно вычислять независимо в каждом потоке. Общую трудоемкость параллельного метода прогонки (p – число процессоров, m – число полос в матрице) можно оценить как . Показатели ускорения  и эффективности   в соответствии с [7] оцениваются по формулам:

Существуют различные подходы для организации параллельных вычислений на вычислительных системах с общей памятью. Авторами использованы технологии организации параллельных вычислений на основе потоков (класс Thread из библиотеки .NET), предполагающие ручное управление аспектами распараллеливания, и технологии OpenMP, использующей встроенную библиотеку организации распараллеливания.

Организация параллельной обработки данных с использованием потоков предполагает, что программист сам устанавливает сколько данных организуется в тот или иной поток, как он работает. Это трудоемкий процесс, но в некоторых случаях это позволяет четко контролировать процесс вычислений и производить его мониторинг.

Организация распараллеливания расчетов с использованием технологии OpenMP предполагает использование библиотечных процедур, специально предназначенных для разработки многопоточных приложений, функционирующих на многопроцессорных системах с общей памятью [8].

Таким образом, с одной стороны, в работе реализованы различные алгоритмы для распараллеливания метода трехдиагональной прогонки, с другой стороны эти алгоритмы используют различные параллельные вычислительные технологии.

Для выполнения численного эксперимента было разработано две программы в среде программирования Visual Studio 2017: на языке программирования С# с использование технологии Thread., на языке программирования C++ с использованием технологии OpenMP.

В результате выполненного вычислительного эксперимента по исследованию эффективности параллельных алгоритмов для решения систем линейных уравнений с трехдиагональной матрицей коэффициентов при неизвестных были измерены время работы T (сек, мсек) и ускорение S работы параллельных алгоритмов относительно последовательных алгоритмов.

Применение системы расчета рассмотрено на тестовых данных, например, для решения задачи распределения температуры при заданных начальных и краевых условиях. Тестирование было проведено на одномерной задаче теплопроводности с неявной схемой аппроксимации.

Размерность задачи варьировалась для значений N от 1.0E+04 до 4.2E+07 в направлении x. Задача была рассчитана в различных сочетаниях количества Thread – потоков и OpenMP-потоков.

Результаты сравнения времени расчета последовательного и параллельного алгоритмов встречной прогонки показали, что эффект ускорения расчетов заметен для размерностей задачи N> 2⋅10⁶. Величина ускорения достигает предельного значения S ≈ 1.6 для N> 9×10⁶. Дальнейшее увеличение размерности массива не приводит к увеличению величины ускорения расчетов.

В случае блочного алгоритма сокращение времени расчета за счет увеличения числа потоков при использовании технологии Thread заметно для размерностей N> 2.4×10⁷ (см. рисунок 1а). При использовании OpenMP - технологии эффект ускорения достигается для N, меньших на порядок, а общее время работы алгоритма сокращается примерно в 3-5 раз (см. рисунок 1б). При больших N эффективность распараллеливания очевидна и стремится к теоретическому максимуму.

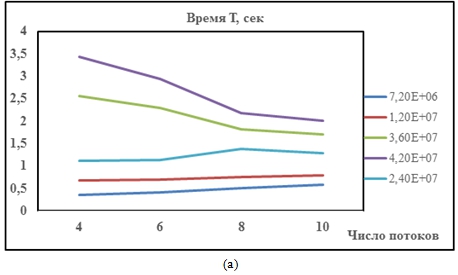
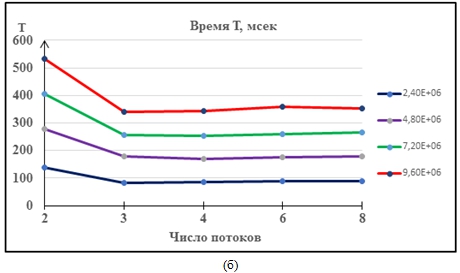
Рис. 1 – Время работы алгоритма блочной прогонки в зависимости от числа потоков p и размерности задачи N: (a) - технология Thread, (б) - технология OpenMP

Заключение

Разработанное программное обеспечение было апробировано на практических занятиях со студентами при изучении темы «Автоматизированные системы научных исследований» для моделирования процесса массопереноса с использованием распределенных вычислений. Это позволило в рамках одного программного продукта в динамике отслеживать развитие изучаемого процесса с возможностью изменять параметры задачи.

Предлагаемый подход и, соответственно, методы станут более востребованы для решения задач, когда помимо проведения самих расчётов особое значение приобретает и параллельная визуализация результатов расчета для того, чтобы можно было наглядно видеть то, каким образом идут вычисления. Исследователь получает средство, которое позволяет в реальном времени с использованием технологий параллельных расчетов получать визуальный результат моделирования процесса распространения температуры в исследуемой области.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Воеводин В.В. Параллельные вычисления/ В.В. Воеводин, Вл. В. Воеводин – СПб.: БХВ-Петербург, 2002. – 608с.
2. Гергель В.П. Основы параллельных вычислений для многопроцессорных вычислительных систем./ Гергель В.П., Стронгин Р.Г. – Н. Новгород, Изд-во ННГУ, 2003. – 178 с.
3. Гергель В.П. Теория и практика параллельных вычислений./ Гергель В.П. – М.: БИНОМ, 2007. – 424 с.
4. Яненко Н.Н. Об организации параллельных вычислений и «распараллеливании» прогонки / Яненко Н.Н., Коновалов А.Н., Бугров А.Н., Шустов Г.В. // Численные методы механики сплошной среды. 1978.Т.9. №7. С.139–146.
5. Образовательный комплекс «Параллельные численные методы» Лекционные материалы Баркалов К.А. [Электронный ресурс] Нижегородский государственный университет им. Н.И. Лобачевского Факультет вычислительной математики и кибернетики 2011 г. URL: http://www.hpcc.unn.ru/?doc=491. (дата обращения: 16.02.2020)
6. Ильин С.А. Распараллеливание схемы покомпонентного расщепления для численного решения уравнения теплопроводности . Ильин С.А., Старченко А.В.// Параллельные вычислительные технологии (ПаВТ-2015): Труды международной научной конференции (Екатеринбург, 2015 г.). Челябинск: ЮУрГУ, 2015. С. 399–402.
7. Федоров А. А. Метод двухуровневого распараллеливания прогонки для решения трехдиагональных линейных систем на гибридных ЭВМ с многоядерными сопроцессорами, . Федоров А. А., Быков А. Н. // Вычислительные методы и программирование, 2016, Т.17, вып. 3, С 234 – 244.
8. Антонов А. С. Параллельное программирование с использованием технологии OpenMP: учебное пособие / А. С. Антонов // М.: Издательство МГУ, 2009. – 77 с.
9. Головашкин Д.Л.Ускорение вычислений по блочным алгоритмам разностного решения уравнения теплопроводности. СБОРНИК ТРУДОВ ИТНТ . Головашкин Д.Л., Яблокова Л.В. Резник И.Д. – 2019. С. 601–607.

Список литературы на английском языке / References in English

1. Voevodin V.V. Parallel'nyye vychisleniya [Parallel computing] / V.V. Voevodin, Vl. V. Voevodin – St. Petersburg: BHV-Petersburg, 2002. – 608 p. [in Russian]
2. Gergel V.P. Osnovy parallel'nykh vychisleniy dlya mnogoprotsessornykh vychislitel'nykh sistem [Basics of parallel computing for multiprocessor computing systems]./. Gergel V.P., Strongin R.G. – N. Novgorod, Nizhny Novgorod State University Publishing House, 2003. – 178 p. [in Russian]
3. Gergel V.P. Teoriya i praktika parallel'nykh vychisleniy [Theory and practice of parallel computing]./. Gergel V.P. – M.: BINOM, 2007. – 424 p. [in Russian]
4. Yanenko N.N. Ob organizatsii parallel'nykh vychisleniy i «rasparallelivanii» progonki [Ob organizatsii parallel'nykh vychisleniy i «rasparallelivanii» progonki [On organization of parallel computing and the parallelization of sweep] // Chislennyye metody mekhaniki sploshnoy sredy [Computational methods of continuum mechanics]. / Yanenko N.N., Konovalov A.N., Bugrov A.N., Shustov G.V. – 1978. – V.9. – No. 7. – P.139-146. [in Russian]
5. Obrazovatel'nyy kompleks «Parallel'nyye chislennyye metody» Lektsionnyye materialy Barkalov K.A. [“Parallel numerical methods” Educational complex. Lecture materials by K. Barkalov] [Electronic resource] Lobachevsky Nizhny Novgorod State University, Faculty of Computational Mathematics and Cybernetics 2011. URL: http://www.hpcc.unn.ru/?doc=491 (accessed: 16.02.2020) [in Russian]
6. Ilyin S.A. Rasparallelivaniye skhemy pokomponentnogo rasshchepleniya dlya chislennogo resheniya uravneniya teploprovodnosti [Parallelization of componentwise splitting scheme for the numerical solution of the heat equation] / Ilyin S.A., Starchenko A.V. // Parallel'nyye vychislitel'nyye tekhnologii (PaVT-2015): Trudy mezhdunarodnoy nauchnoy konferentsii (Yekaterinburg, 2015 g.). [Parallel computing technologies (PaVT-2015): Proceedings of the international scientific conference (Yekaterinburg, 2015)]. Chelyabinsk: SUSU], 2015. P. 399–402. [in Russian]
7. Fedorov A. A. Metod dvukhurovnevogo rasparallelivaniya progonki dlya resheniya trekhdiagonal'nykh lineynykh sistem na gibridnykh EVM s mnogoyadernymi soprotsessorami [Method of two-level parallelization of sweep for solving tridiagonal linear systems on hybrid computers with multi-core coprocessors] / Fedorov A. A., Bykov A. N. // Vychislitel'nyye metody i programmirovaniye [Computational Methods and Programming], – 2016, – V.17, – No. 3, – P. 234 - 244. [in Russian]
8. Antonov A. S. Parallel'noye programmirovaniye s ispol'zovaniyem tekhnologii OpenMP: uchebnoye posobiye [Parallel programming using OpenMP technology: training manual] / A. S. Antonov // M.:Moscow State University, 2009. – 77 p. [in Russian]
9. Golovashkin D.L. Uskoreniye vychisleniy po blochnym algoritmam raznostnogo resheniya uravneniya teploprovodnosti [Acceleration of computations by block algorithms for difference solution of the heat equation]./ Golovashkin D.L., Yablokova L.V. Reznik I.D. // Collection of works of ITNT– 2019. – P. 601–607. [in Russian]