ПОДГОТОВКА БУДУЩИХ ПСИХОЛОГОВ К РЕШЕНИЮ ИССЛЕДОВАТЕЛЬСКИХ ЗАДАЧ С ПОМОЩЬЮ ПАРАМЕТРИЧЕСКИХ КРИТЕРИЕВ

Гришкина Т.Е.

 Старший преподаватель, Амурский государственный университет

ПОДГОТОВКА БУДУЩИХ ПСИХОЛОГОВ К РЕШЕНИЮ ИССЛЕДОВАТЕЛЬСКИХ ЗАДАЧ С ПОМОЩЬЮ ПАРАМЕТРИЧЕСКИХ КРИТЕРИЕВ

Аннотация

В статье представлена актуальность применения методов математической статистики в психолого-педагогических исследованиях. Рассмотрены некоторые методы проверки соответствия эмпирических данных нормальному закону распределения. На конкретных примерах показан процесс подготовки будущих психологов к решению исследовательских профессиональных задач с помощью параметрических критериев.  Материалы статьи могут использоваться в диссертационных исследованиях, при выполнении выпускных квалификационных работ, курсовых работ бакалавров психолого-педагогического образования, бакалавров психологов.

Ключевые слова: психолого-педагогические исследования, параметрические критерии, нормальный закон распределения.

Grishkina Т.Е.

Senior Lecturer, Amur State University

TRAINING OF FUTURE PSYCHOLOGISTS IN SOLVING THE RESEARCH PROBLEMS WITH PARAMETRIC CRITERIA

Abstract

The paper presents the relevance of the use of mathematical statistics methods in psychological and pedagogical studies. Some methods for verifying the correspondence of empirical data to the normal distribution law are considered. The specific examples show the process of preparing future psychologists in solving research problems using parametric criteria. The materials of this work can be used in dissertational studies, at preparation of final qualification works, courseworks of bachelors in psychological and pedagogical education, bachelors in psychologists.

Keywords: psychological and pedagogical studies, parametric criteria, normal distribution law.

Методы математической статистики находят применение во многих областях психологии и педагогики в качестве инструмента, необходимого для проведения обработки результатов исследований различного характера. Подтверждением этого является: включение дисциплин «Методы прикладной статистики», «Математические методы в психологии», «Статистические методы в педагогических исследованиях» в учебные планы по направлениям подготовки «Психолого-педагогическое образование», «Психология»; обязательное использование статистической обработки результатов психологического, педагогического эксперимента в диссертационных исследованиях.

Популярность математических методов в педагогических исследованиях обуславливается тем, что благодаря использованию количественных методов удается дать оценку качественным психолого-педагогическим параметрам [1, C. 40].

Вопрос о корректности применения различных процедур и методов  обработки результатов психолого-педагогического исследования является на данный момент  актуальным, так как неправильный выбор критериев, влечет за собой ошибочные выводы и сводит на нет всю проведенную работу по сбору и обработке эмпирического материала.

В математической статистике для решения исследовательских задач, используются специальные методы, называемые критериями различий, которые делятся на параметрические – включающие в формулу расчета средние и дисперсии и непараметрические – основанные на оперировании  частотами или рангами.

В нашей статье остановимся подробнее на параметрических критериях различий. При изучении темы «Параметрические критерии» в рамках вышеперечисленных дисциплин, необходимо учесть следующие моменты: означенные критерии возможно использовать только при следующих условиях: измерение должно быть проведено в шкале интервалов и отношений, данные подчиняются нормальному закону распределения, их число достаточно.

Существует несколько методов проверки выборки на нормальность:

1. Осуществляется построение полигона частот (ломаная, отрезки которой соединяют точки (х_i, n_i), где первая координата – варианта, вторая – соответствующая частота) и кривой эмпирической функции нормального распределения. Если распределение починяется нормальному, то графики практически совпадают.
2. Вычисляется среднее, медиана (варианта, которая делит вариационный ряд на две части, равные по числу вариант) и мода (наиболее часто встречающаяся варианта). Если эти три значения достаточно близки распределение считается нормальным.
3. Вычисляются эксцесс и асимметрия нормальной кривой распределения, если эти две числовые характеристики приблизительно равны нулю, то распределение близко к нормальному.
4. Вычисляют среднее и стандартное отклонение и сравнивают теоретические результаты с эмпирическими. Если выборка подчиняется нормальному закону распределения, то: 25% выборочных данных должно принадлежать интервалу ; 50% − ; 75% − ; 100% − .
5. Использование критериев согласия распределений: χ²− критерий Пирсона, λ − критерий Колмогорова - Смирнова.

В психологических исследованиях нормальное распределение используется в первую очередь при разработке  и применении тестов интеллекта и способностей [2, С. 54]. Применительно к другим психологическим признакам сопоставление с нормальным законом распределения является весьма дискуссионным. Известно, что в реальных психологических экспериментах редко получаются данные, распределённые строго по нормальному закону. Однако, результаты исследований проводимых с помощью параметрических критериев отличаются большей достоверностью и если соблюдены все условия осуществления корректной обработки данных психологического эксперимента, то целесообразно воспользоваться именно представленным инструментарием.

К параметрическим критериям относят:

1. t-критерий Стьюдента.

Применяется: а) для сравнения выборочной средней  с некоторым известным числовым значением a₀.

Эмпирическое значение критерия рассчитывается по формуле:

, при неизвестной дисперсии генеральной совокупности; , если  известно, где S – исправленное стандартное отклонение; n – объем выборки,  – известная дисперсия генеральной совокупности.

Для поиска критических значений используют таблицу распределения Стьюдента (по уровню значимости  и  числу степеней свободы  k = n – 1).

б) для обнаружения различия между средними значениями  двух выборок.

Наблюдаемое значение t-критерия рассчитывается по формуле:

• для независимых выборок

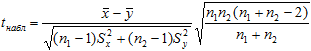где  – выборочная дисперсия 1 выборки  – выборочная дисперсия 2 выборки; n₁ – объем 1 выборки; n₂ – объем 2 выборки.

• для зависимых выборок

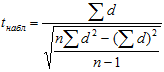
 d − разность «после» минус «до»; n− число пар данных в зависимых выборках.

Для поиска критических значений используют таблицу распределения Стьюдента (по уровню значимости α и числу степеней свободы  k = n₁+n₂ –2 для независимых выборок, k = n–1 для зависимых выборок).

Приведем практические примеры, которые можно предложить решить  студентам в рамках занятия «Математические методы в психологии», как исследовательские профессиональные задачи.

Пример 1. Среди учащихся одной группы детского сада, было проведено исследование на тему: «Психолого-педагогическая коррекция агрессивного поведения дошкольников». В целях этого исследования была проведена методика: Диагностика «Кактус». Так как целью теста было определить уровень агрессии, в первую очередь оценивались такие показатели, как наличие и длина иголок, тип линий и преобладающие цвета. Каждому показателю присваивались определённые баллы, после чего баллы суммировались и определялся уровень агрессии. 0-2 баллов – низкий уровень агрессии; 3-5 – средний уровень агрессии; 6-7 – высокий уровень.

Данные диагностики подразделялись на две группы: до проведения коррекционной программы и после проведения.

До проведения психокоррекции были получены следующие данные (буквы –  инициалы, цифры – баллы): АМ 3; БН 3; ВС 1; ДА 5; ИТ 5; КК 4; КЕ 3; КТ 6; ЛЗ 4; МР 5; НГ 2; НП 5; ПА 4; РО 3; СА 7; СВ 4; ФЯ 2; ЦК 4;

ЧД 1; ЮА 4. После: АМ 2; БН 3; ВС 1; ДА 4; ИТ 5; КК 3; КЕ 2; КТ 6; ЛЗ 3; МР 6; НГ 2; НП 3; ПА 2; РО 3; СА 5; СВ 3; ФЯ 2; ЦК 3; ЧД 1; ЮА 3.

Исследователя интересует вопрос: является ли коррекционная программа эффективной?

Предварительным этапом решения задачи выступает выражение в процентном соотношении уровня агрессии: (до) высокий – 10% , средний – 70%, низкий – 20%; (после) высокий – 10%, средний – 55%; низкий – 35%.

После формулировки задачи и предварительного этапа решения, в группе обсуждаются методы необходимые для проведения исследования и план решения. Студентам предлагается самостоятельно проверить выборки на нормальность, используя различные подходы. Например, вычислить среднее, моду, медиану, эксцесс и асимметрию выборочных данных. Эти вычисления могут быть произведены «вручную» (на практическом занятии) и с помощью MS Excel или Statistica (на лабораторном занятии).

Итак, первая выборка: =3,75; М₀=4; M_e=4; E=-0,03; А=-0,006; вторая: =3; М₀=3; M_e=3,1; E=-0,009; А=0,033.

Сравнив полученные с помощью разных методов результаты, приходим к выводу: выборки подчиняются нормальному закону распределения, следовательно, возможно использовать t-критерий Стьюдента для зависимых выборок.

Сформулируем гипотезы:

Н₀: общий уровень агрессии не изменился, психокоррекционная программа не эффективна;

H₁: уменьшение уровня агрессии статистически значимо; психокоррекционная программа эффективна.

После проведения необходимых вычислений, получено: t_набл=3,58. Критическое значение t_кр  (предлагается  найти  с помощью: таблиц распределения Стьюдента в справочниках; модуля «Вероятностный  калькулятор» в программе Statistica), по уровню значимости α=0,01 и числу степеней свободы k =19: t_кр=2,86.

Так как t_набл> t_кр, то принимаем гипотезу H₁ − уменьшение уровня агрессии статистически значимо; психокоррекционная программа эффективна.

Пример 2. Для изучения эффективности программы по повышению уровня адаптации первоклассников к школе, было проведено исследование оценки  школьной мотивации до и после проведения программы. В эксперименте принимало участие 15 человек (табл. 1).

 

Таблица 1 – Результаты исследования

№	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
До	7	14	13	12	16	15	17	19	18	18	16	20	23	24	22
После	16	15	15	14	19	20	21	25	20	22	20	25	24	26	25

 

Оценить эффективность программы.

Вычислим среднее, моду, медиану, эксцесс и асимметрию:

1-ая выборка: =16,9; М₀=16; M_e=17; E=0,4; А=-0,4;

2-ая выборка =20,5; М₀=20; M_e=20; E=-1,2; А=0,2.

Обратим внимание на то, что первые три характеристики в каждой выборке приблизительно равны, но делать выводы о близости распределения к нормальному на основании одного метода проверки ошибочно, так как уже значения следующих числовых характеристик указывают на сильное отличие выборок от нормальной. Осуществив реализацию всех методов поверки приходим к следующему заключению: при решении данной задачи применение параметрических критериев для проверки статистической значимости будет являться некорректным.

С проведением психолого-педагогических исследований бакалавры встретятся не только в своей будущей профессиональной деятельности, но и при выполнении курсовых, дипломных работ, поэтому развитие навыков и умений решения прикладных исследовательских задач методами математической статистики на практических и лабораторных занятиях является неотъемлемой частью процесса подготовки будущих психологов.

Список литературы / References

1. Двоерядкина Н.Н., Гришкина Т.Е. Использование ROC-кривых в психолого-педагогических исследованиях / Двоерядкина Н.Н., Гришкина Т.Е. // Международный научно-исследовательский журнал. – 2016.– №5(47). Часть 4.– С. 40– 42.
2. Ермолаев О.Ю. Математическая статистика для психологов: учебник / О.Ю. Ермолаев. – 3-е изд., испр. – М.: Московский психолого-социальный институт: Флинта, 2004. – 336 с.

Список литературы на английском языке / References in English

1. Dvoerjadkina N.N., Grishkina T.E. Ispol'zovanie ROC-krivyh v psihologo-pedagogicheskih issledovanijah [The use of ROC-curves in psychological and pedagogical research]/ Dvoerjadkina N.N., Grishkina T.E. // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal. – 2016.– №5(47). ch 4.– P. 40– 42. [in Russian]
2. Ermolaev O.Ju. Matematicheskaja statistika dlja psihologov: uchebnik [Mathematical statistics for psychologists: a textbook] / O.Ju. Ermolaev. – 3nd edition., ispr. – M.: Moskovskij psihologo-social'nyj institut: Flinta, 2004. – 336 p. [in Russian]