МАТЕМАТИКА И СМЕШАННОЕ ОБУЧЕНИЕ. СОХРАНИЛОСЬ ЛИ КАЧЕСТВО ОБУЧЕНИЯ?

Никольская Г.А. ¹, Новоселова Г.П. ¹

¹ Томский политехнический университет

МАТЕМАТИКА И СМЕШАННОЕ ОБУЧЕНИЕ. СОХРАНИЛОСЬ ЛИ КАЧЕСТВО ОБУЧЕНИЯ?

Аннотация

В статье обсуждаются особенности обучения в смешанной модели с Web-поддержкой на платформе Moodle. По результатам проведенного опроса среди студентов делается вывод о предпочтении студентами дисциплины с электронным сопровождением. Выявляются положительные стороны и недостатки смешанной модели с их точки зрения. Проводится сравнительный анализ результатов освоения дисциплины в рамках традиционной и смешанной модели. Отмечается достижение равномерной работы студентов в семестре, повышение их заинтересованности.

Ключевые слова: математика, смешанная модель обучения, опрос.

Nikolskaya G.A. ¹, Novoselova G.P. ¹

¹ Tomsk Polytechnic University

MATHEMATICS AND BLENDED LEARNING. WHAT ABOUT QUALITY?

Abstract

The article considers two models of the mathematics learning. Teaching are made with Web-course support in Moodle named blended learning. Peculiarity of it is discussed. The survey conducted among the students. It concludes preference discipline students with electronic accompaniment. Reveals its positives and disadvantages from the point of view of the students. A comparative analysis of the outcomes is made within the traditional and blended learning model. It is noted the achieving uniform work of students in the semester and increasing their interest.

Keywords: mathematics, blended learning, survey.

Традиционно широкая базовая подготовка в Российской школе позволяла быстро адаптироваться выпускникам к изменяющимся условиям рынка труда и новым технологиям. При этом выпускники вузов имели слабый навык практической работы, связанный с их специальностью, что требовало доучивать молодого специалиста на производстве. Такая образовательная схема плохо вписывается в рыночные условия, в которые все больше погружаются Российские вузы. Современному рынку туда требуются выпускники, готовые немедленно применять свои профессиональные навыки. Российская система образования вынуждена внедрять инновации и новые образовательные технологии, чтобы соответствовать новым экономическим условиям, при этом стараясь сохранить традиции российской школы.

Одним из вариантов выхода из этой ситуации университеты видят в интенсификации процесса обучения. На помощь приходят инновации в педагогике. Образовательная инновационная технология, как устоявшаяся форма организации учебного процесса, должна на уровне нормативного документа гарантировать воспроизведение сходных результатов в одних и тех же образовательных условиях, включая некоторые новшества методического, организационного, технического характера. Одна из таких интенсивно внедряемых технологий – технология смешанного обучения (b-learning).

В отличие от традиционной формы обучения, b-learning предполагает часть работы проводить в интернет-среде. Туда может быть вынесена методическая литература, тренажеры, обучающие и контролирующие тесты и др. Несмотря на интенсивное внедрение b-learning в учебный процесс, преподаватели-математики скептически относятся к возможности изучать высшую математику с помощью инструментов e-learning. Главным образом, это связано с низкой эффективностью приобретения студентами предметных навыков и умений. В ряде университетов математики принципиально отказываются от методов b-learning, где-то электронная среда используется лишь для размещения методических материалов и играет роль электронной библиотеки. И только единицы делегируют e-learning задачи развития вычислительных навыков и умений использования аппарата анализа.

Целью данной работы является обсуждение результатов нашего опыта использования возможностей b-learning в рамках учебного процесса по математике и отношения студентов к разным формам учебного процесса.

В Томском политехническом университете смешанная форма обучения в течение трех лет активно внедряется в учебный процесс. Его концептуальная часть находится в разработке. Поэтому в реализации b-learning на сегодняшний день наблюдается некоторая стихийность. Но это дает возможность преподавателям выбирать удобные для них формы оценивания, способы взаимодействия со студентами, делегировать любую часть курса в Moodle портал, пробовать новые обучающие инструменты. Поэтому, мы постоянно контролируем результаты своей деятельности, пытаясь сохранить ценное от традиционной системы образования и избежать ухудшения результатов обучения. Ответственность за реализацию программы обучения и за применение новой формы обучения несет преподаватель. Со стороны университета оказана существенная поддержка: выделен ресурс в среде Moodle, разработана система технической поддержки для преподавателей-создателей Web курсов, все студенты интегрированы в корпоративную электронную среду и имеют доступ к обучающим средствам, размещенным на сайтах университета.

Для исследования привлекательности и эффективности электронного сопровождения в процессе изучения дисциплины «математика» был проведен опрос студентов первого и второго курсов. Студенты изучали различные дисциплины, в том числе и математические, в традиционной форме и с использованием Web составляющей. Цель опроса – выяснить отношение студентов к смешанной форме обучения и их мнение относительно составляющих элементов Moodle курса. Aнализ проводился в трех направлениях: а) привлекательность, б) полезность, в) необходимость контакта с преподавателем. После завершения семестра студентам было предложено ответить на вопросы анкеты.

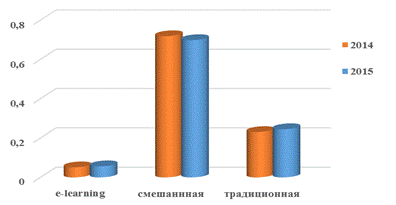
На рисунке 1 представлен один из результатов опроса первокурсников о предпочтении формы изучения математической дисциплины. Как видно из рисунка, большая часть студентов склоняется к форме обучения с использованием электронной части курса, что соответствует результатам работы [1]. Причем отличия между результатами опросов 2014 и 2015 годов менее двух процентов. Очевидно, большую роль в выборе формы изучения дисциплины играет привлекательность интернета и элемент игры в достаточно сложном предмете.

Рис. 1 – Диаграмма частот ответов на вопрос: какую форму изучения вы бы предпочли?

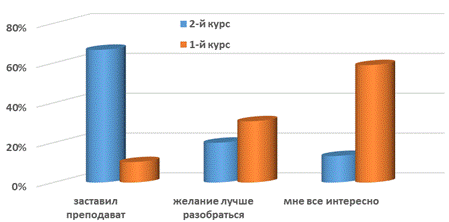
По мере усложнения дисциплин, студенты начинают иначе относиться и к форме работы, и к результату, и к затраченным усилиям. На рисунке 2 приведены результаты ответов на вопрос о причинах выбора курса с электронным сопровождением. Как видно из рисунка, студенты 2-го курса относятся к процессу обучения прагматично.

Рис. 2 – Сравнение причин использования электронного курса

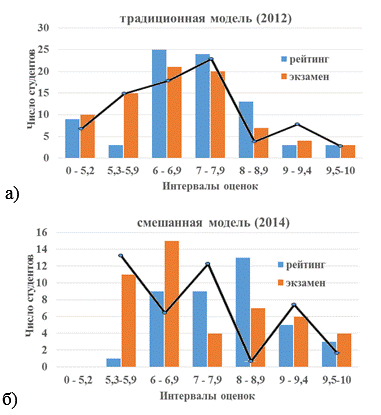
Преподавателей же в большей мере интересует качественный результат. Цели ставились следующие: систематизировать работу студентов в семестре, обеспечить минимальный уровень навыков решения задач, обеспечить прозрачность оценивания, стимулировать работу студентов на всех этапах изучения курса. На рисунке 3 приведены диаграммы рейтинговых семестровых оценок в сравнении с экзаменационными оценками в первом семестре за два года обучения: в 2012 г. в традиционной модели и в 2014 г. в смешанной модели. В ТПУ используется накопительная система оценивания, согласно которой результирующая оценка складывается из семестрового рейтинга (60 баллов) и экзаменационной оценки (40 баллов). Для удобства сравнения оценки приведены к единой 10-бальной шкале. Здесь же приведены оценки за курс – сумма рейтинговой и экзаменационной оценок.

Как видно из рисунка, цель систематизировать и стимулировать работу студентов в семестре была достигнута. Распределение рейтинговой оценки смещено в сторону больших значений, по сравнению с обучением в традиционной модели. По сравнению с традиционной формой (2012 г.) средний рейтинг вырос. Это связано с возможностью выполнять оцениваемые задания в любое удобное время, а также, с возможностью многократно повторять контролируемые задания, повышаю свою оценку. Аналогичная систематизация активной работы студентов отмечается в [2].

Рис. 3. – Диаграммы семестрового рейтинга (), экзаменационной оценки () и суммарной оценки (─): а) в традиционной модели; б) в смешанной модели

Возможность повысить оценку стимулирует работу студентов. Однако, значительного улучшения знаний не произошло. Распределение экзаменационной оценки смещено в сторону низших значений. С одной стороны, это результат сознательного решения студентов, когда в условиях прозрачности системы оценивания можно запланировать окончательный семестровый результат и, при условии высокого, но не достаточного до «отлично» рейтинга, готовиться с минимальными усилиями на «хорошо». При условии высокого семестрового балла это приводит к некачественной подготовке к экзамену. Как видно из диаграммы (б), наибольшее количество всех оценок – это оценки низшего уровня: «отлично» – 9, «хорошо» – 7 и «удовлетворительно» – 5. В традиционной модели обучения распределение результатов работы в семестре и на экзамене более связное, имеет вид нормального распределения и сходную структуру.

Заключение. Таким образом, на основании проведенных опросов и анализа результатов обучения можно сделать следующие выводы.

1. Смешанная модель обучения наиболее предпочтительна с точки зрения студентов. Она позволяет изучать запланированный материал с удобной скоростью, выполнять контролирующие мероприятия по мере готовности и не обязательно в аудитории, иметь постоянный доступ к учебно-методическим материалам.
2. Сравнительный анализ результатов обучения посредством анализа распределений рейтинговых-семестровых, экзаменационных и суммарных оценок в традиционной и в смешанной модели показал не вполне удовлетворительный результат, который мы связываем с неосознанной реализацией студентами возможности «запланировать» результирующую оценку за курс при наименьших усилиях.
3. Переход на смешанную модель обучения математическим дисциплинам требует концептуального подхода в подготовке Web-составляющей курса, проверенных экспериментально и обоснованных психологами обучающих и контролирующих элементов курса.

Литература

1. Imas O., Kaminskaya V., Sherstneva A. Teaching Math Through Blended Learning // International Conference on Interactive Collaborative Learning (ICL), 20-24 September 2015, Florence, Italy. – – pp. 511-514.
2. Sherstneva,I., Imas, O.N., Galanova, N.Yu., Tran V.T. Influence of Evaluation System on Effectiveness of Foreign Students’ Mathematical Education // Procedia – Social and Behavioral Sciences. – 2015. – V 215. – pp. 181–184.