ИСПОЛЬЗОВАНИЕ ROC-КРИВЫХ В ПСИХОЛОГО-ПЕДАГОГИЧЕСКИХ ИССЛЕДОВАНИЯХ

Двоерядкина Н.Н.¹, Гришкина Т.Е.²

  ¹Кандидат педагогических наук, доцент; ²Старший преподаватель, Амурский государственный университет

ИСПОЛЬЗОВАНИЕ ROC-КРИВЫХ  В ПСИХОЛОГО-ПЕДАГОГИЧЕСКИХ ИССЛЕДОВАНИЯХ

Аннотация

В статье представлена необходимость использования методов математической статистики в психолого-педагогических исследованиях. Продемонстрированы случаи некорректного применения непараметрических критериев для проверки статистических гипотез. Рассматриваются возможности использования ROC-кривых в психолого-педагогических исследованиях. Строятся ROC-кривые для сравнения качества двух непараметрических критериев. Определяется показатель AUC на конкретном примере. Материалы статьи могут использоваться в диссертационных исследованиях и при выполнении выпускных квалификационных работ бакалавров психолого-педагогического образования.

Ключевые слова: психолого-педагогические исследования, ROC- кривые, непараметрические критерии.

 Dvoeryadkina N.N.¹, Grishkina T.E.²

¹PhD in Pedagogy, Associate professor; ²Senior lecturer, Amur State University

USE THE ROC-CURVES IN PSYCHOLOGICAL AND  PEDAGOGICAL RESEARCH

Abstract

The article describes the need to use mathematical statistics methods in psychological and  pedagogical research. Showcased are cases of improper use of nonparametric tests for testing statistical hypotheses. We consider possibilities of use the ROC-curves in the within the psychological and pedagogical investigations. Constructing the ROC-curve for comparing the quality of two nonparametric tests. Determined AUC ratio on concrete example. Article may be use in the dissertation research and in the performance of final qualifying works of bachelors of psychological and pedagogical education.

Keywords: psychological and pedagogical research, ROC-curve, nonparametric tests.

В процессе психолого-педагогических исследований происходит изучение какой-либо педагогической действительности. В результате анализа исследователь выдвигает тот или иной факт педагогической действительности, который отвергает или подтверждает в процессе своей работы. Существуют эмпирические, теоретические и математические методы педагогического исследования.

Математические методы в педагогических исследованиях становятся всё более популярными. Подтверждением этого являются и обязательное использование математической обработки результатов педагогического эксперимента в диссертационных исследованиях, и включение дисциплин вида «Методы прикладной статистики», «Математическое моделирование социально-экономических процессов», «Статистические методы в педагогических исследованиях» в учебные планы подготовки бакалавров по направлению подготовки «Психолого-педагогическое образование».

Популярность математических методов в педагогических исследованиях обуславливается тем, что благодаря использованию количественных методов удается дать оценку качественным психолого-педагогическим параметрам. Выводы и заключения, полученные с помощью методов математической статистики, позволяют лаконично описать характеристики сложных педагогических процессов. Кроме того, математические методы позволяют избежать субъективной оценки доказываемых фактов действительности. Ведь «математику», в отличие от «педагога», совершенно неважно, что за числами 0 и 1, например, скрываются гендерные различия наблюдаемых. Он проводит соответствующий анализ данных ему числовых значений и в результате расчетов получает также числовое значение. И только «педагог» должен дать качественную интерпретацию полученной количественной величины с учетом гендерных различий.

Среди всех математических методов в психолого-педагогических исследованиях чаще используются методы проверки статистических гипотез [1]. А среди них при анализе результатов педагогического эксперимента из-за специфики исходных данных приходится применять непараметрические критерии, которые не требуют больших объемов выборки и нормальности распределения. На сегодняшний день описано достаточно большое количество непараметрических критериев, подходящих для проверки статистических гипотез.

Каждому параметрическому критерию соответствует два и более непараметрических аналога. Например, если данные подчиняются нормальному распределению, то для равенства средних двух выборок используют критерий Стьюдента. Если необходимо сравнить средние значения для независимых выборок, законы распределения которых неизвестны, то можно использовать критерии Манна-Уитни или Q критерий Розенбаума [2].

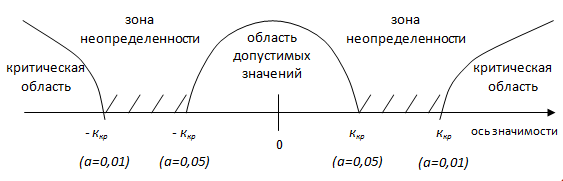
Проверка статистических гипотез осуществляется по стандартной схеме с использованием графического изображения области допустимых значений (область принятия нулевой гипотезы), критической области (область принятия альтернативной гипотезы) и зоны неопределенности (рис.1).

Рис. 1 - Ось значимости

 

Для некоторых непараметрических критериев (G-знаков, Т-Вилкоксона и др.) области допустимых значений и критическая меняются местами.

Принятие решений по данному рисунку общеизвестно: если наблюдаемое значение критерия попадает в область допустимых значений или в критическую область, то приходится говорить о справедливости нулевой или альтернативной гипотезы соответственно. Неясным остается вопрос: как вести себя в случае, когда наблюдаемое значение лежит в зоне неопределенности или на границе областей. Бесспорно, если есть возможность увеличить объем выборки, то проблема устранится сама по себе, т.к. надежность критерия увеличится. Но чаще всего, увеличить объем выборки невозможно. В этой ситуации исследователь может трактовать полученные результаты в свою пользу или выбрать другой критерий и оценить гипотезу с его помощью, если этот критерий не усугубит ситуацию.

Возникают естественные вопросы, не будут ли полученные таким образом результаты доказываемого факта искажать педагогическую действительность; какой из критериев является более мощным, наверняка дает достоверные результаты и зависит ли чувствительность критерия от выборочных данных.

Возникло противоречие между необходимостью применять методы проверки статистических гипотез в психолого-педагогических исследованиях  и невозможностью в некоторых случаях объективно качественно интерпретировать результаты полученных тестов.

Для ответа на поставленный вопрос нами рассмотрены возможности использования ROC-curve анализа в психолого-педагогических исследованиях.

ROC-анализ находит своё широкое применение в медицине особенно при проведении клинических исследований [3]. Он позволяет указать какая диагностика является для данного заболевания наиболее оптимальной. Основой данного анализа является построение ROC-кривой, которая показывает зависимость количества верно классифицированных положительных примеров от количества неверно классифицированных отрицательных примеров [4].

Построим ROC-кривую для сравнения двух непараметрических критериев: G-знаков и Т-Вилкоксона. Выбор этих критериев обусловлен тем, что ограничения данных критериев по объему выборки идентичны. Построения выполним на условном примере, в котором необходимо сравнить две зависимые выборки малого объема. Пусть анализируются результаты тестов у 11 студентов до и после проведения психологического тренинга, нулевые сдвиги отсутствуют (табл. 1).

Таблица 1 - Результаты тестирования

	1	2	3	4	5	6	7	8	9	10	11
«До»	4	3	2	2	4	5	3	3	4	2	3
«После»	3	4	3	3	3	4	5	5	5	4	5
Сдвиг	-1	+1	+1	+1	-1	-1	+2	+2	+1	+2	+2
Модуль сдвига	1	1	1	1	1	1	2	2	1	2	2
Ранги модулей	4	4	4	4	4	4	10	10	4	10	10

 

G_кр=2 () и G_кр=1 (), G_эмп=3, принимается нулевая гипотеза, т.е. положительный сдвиг случаен.

Т_кр=13 () и Т_кр=7 (), Т_эмп=12, значение попадает в зону неопределенности, значит, нулевую гипотезу отвергаем.

Согласно проведенному статистическому анализу критерий G-знаков позволяет утверждать, что психологический тренинг не повлиял на результаты тестов у данных студентов, а критерий Вилкоксона, напротив, уже отрицает эту гипотезу.  Остается вопросом, согласно какому критерию принимать решение.

Сравним значимости тестов, используемых для представленных данных. Для этого составим из выборочных данных условия задачи различные подвыборки и рассчитаем для каждой из них значения G_эмп , Т_эмп. Найдем соответствующие критические точки, сделаем вывод о справедливости нулевой гипотезы для каждой подвыборки. По полученным результатам построим ROC-кривые для каждого теста.

Так как выбранные критерии начинают работать с объемов в 5 наблюдений, то из исходных данных можно составить всевозможные подвыборки объемом 5 и более наблюдений. Учитывая, что в таблице критических точек для критерия G-знаков критические значения для уровней значимости   и  начинают отличаться друг от друга при объеме в 8 наблюдений, рассмотрим различные подвыборки из 8, 9 и 10 наблюдений из данных 11.

Вычислим количество выборок с использованием формулы числа сочетаний без повторений. Всего получается  выборка, но среди них есть одна выборка, в которой нет нетипичных (в нашем случае отрицательных) сдвигов, значит, для построения ROC-кривой будет использовано 230 наблюдений.

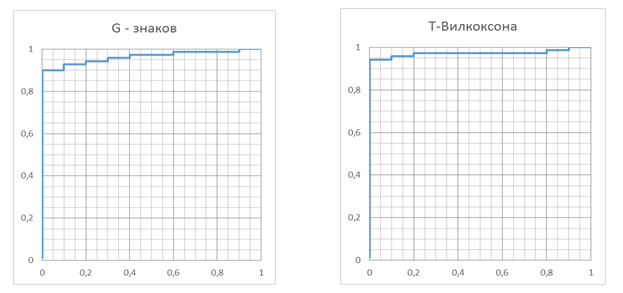
Для «идеального» критерия ROC-кривая проходит через точки (0,0), (0,1) и (1,1). Чем ближе эмпирическая линия к «идеальному» варианту, тем точнее и надежнее тест.

               Рис. 2 - Изображения ROC-кривых

Судить о качестве теста можно по показателю AUC (Area Under Curve), выражающему площадь под данной кривой. Значение данного показателя меняется в диапазоне от 0 до 1 и рассчитывается с помощью численных методов. Если AUC< 0,6, то качество теста считается неудовлетворительным. Для ситуации, представленной на рис.2 значения этого показателя составляет для G-знаков AUC=0,9675, для Т-Вилкоксона AUC=0,9856.

Качество обоих критериев можно оценить, как очень хорошее, но критерий Вилкоксона в данной ситуации является более значимым. Поэтому следует считать достоверными выводы о справедливости нулевой гипотезы, полученные с помощью критерия Вилкоксона.

Литература

1. Юрьева Т.А., Чалкина Н.А., Двоерядкина Н.Н. Подготовка бакалавров психолого-педагогического образования к применению количественных методов исследования с использованием интерактивных форм обучения // Вектор науки Тольяттинского государственного университета. Серия: Педагогика, психология. –  2014. –  № 3. – С. 229-232.
2. Сидоренко Е.В. Методы математической обработки в психологии. – Спб.: ООО «Речь», 2007. – 350 с.
3. Леонов В.П. Логистическая регрессия в медицине и биологии // Биометрика URL: http://www.biometrica.tomsk.ru/logit_1.htm
4. 4. Богданов Л.Ю. Оценка эффективности бинарных классификаторов на основе логистической регрессии методом ROC-анализа // Вестник Саратовского государственного технического университета. – – Т. 4, № 2 (50). – С. 92-97.

References

1. Jur'eva T.A., Chalkina N.A., Dvoerjadkina N.N. Podgotovka bakalavrov psihologo-pedagogicheskogo obrazovanija k primeneniju kolichestvennyh metodov issledovanija s ispol'zovaniem interaktivnyh form obuchenija // Vektor nauki Tol'jattinskogo gosudarstvennogo universiteta. Serija: pedagogika, psihologija. –  2014. –  № 3. – S. 229-232.
2. Sidorenko E.V. Metody matematicheskoj obrabotki v psihologii. – Spb.: OOO «Rech'», 2007. – 350 s.
3. Leonov V.P. Logisticheskaja regressija v medicine i biologii // Biometrika URL: http://www.biometrica.tomsk.ru/logit_1.htm
4. Bogdanov L.Ju. Ocenka jeffektivnosti binarnyh klassifikatorov na osnove logisticheskoj regressii metodom ROC-analiza // Vestnik Saratovskogo gosudarstvennogo tehnicheskogo universiteta. – 2010. – T. 4, № 2 (50). – S. 92-97.